导航卫星自主时间维持算法影响因素分析∗

钦伟瑾 韦 沛 杨旭海 任晓乾

(1中国科学院国家授时中心西安710600)

(2中国科学院精密导航定位与定时技术重点实验室西安710600)

(3中国科学院大学北京100049)

1 引言

星上自主系统时间指的是导航星座在自主运行模式下,所有星载钟采用某种算法共同保持的纸面时间.由于星间双向伪距解算的钟差为相对钟差,缺乏时间参考,不能确定每颗卫星相对时间参考的绝对钟差,随着时间的累积,会出现钟差整体漂移的情况,因此需要建立高准确度和高稳定度的星上系统时间作为参考[1−3].

2 星上自主系统时间计算模式

星上自主系统时间计算模式分为集中模式和分布模式.集中模式的原理是选定一颗主星上的主钟,从星通过星间观测值解算得到星间钟差,然后以通信的方式传给主星,主星利用所有卫星在计算间隔内的钟差信息,根据加权平均算法计算系统时间,以及各星载钟相对系统时间的钟差及钟速,并更新导航电文,经由星间链路发送给其他卫星.拓扑结构如图1所示.集中模式的优点是能够得到统一的时间参考,并且非主星上不需要搭载计算设备,缺点是对主星的依赖性较大.出于连续性考虑,在计算系统时间时尽量做到无缝切换,出于安全性考虑,不仅要对每颗主星上的主钟做热备份,还要对主星做备份.

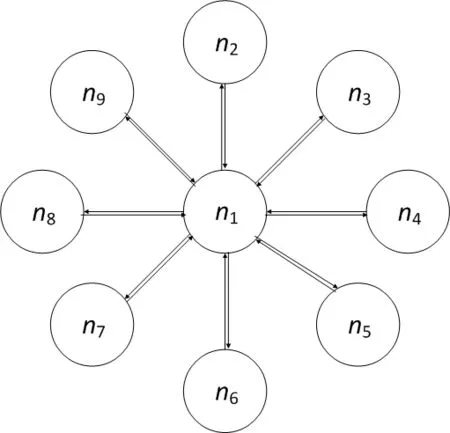
图1 集中模式拓扑结构图Fig.1 Topology structure of centralized model

分布模式与集中模式原理相同,只是不需要选定主星,每颗卫星都参与计算.拓扑结构如图2所示.优点是各颗卫星相对独立,1颗卫星出现问题,不会影响其他卫星,缺点是星上的参考时间不统一,每颗卫星都需要搭载计算设备,加重卫星载荷负担.

分布模式生成的时间参考不唯一,不利于星上自主系统时间的计算和数据分发,因此本文按照图1模式研究星上自主系统时间算法.

3 观测方程

本文是在轨道已知的前提下进行星间时间同步研究的.观测值经过历元归化[4−5]后,在同一时刻接收无线电测距信号,星间观测方程为[6−7]:

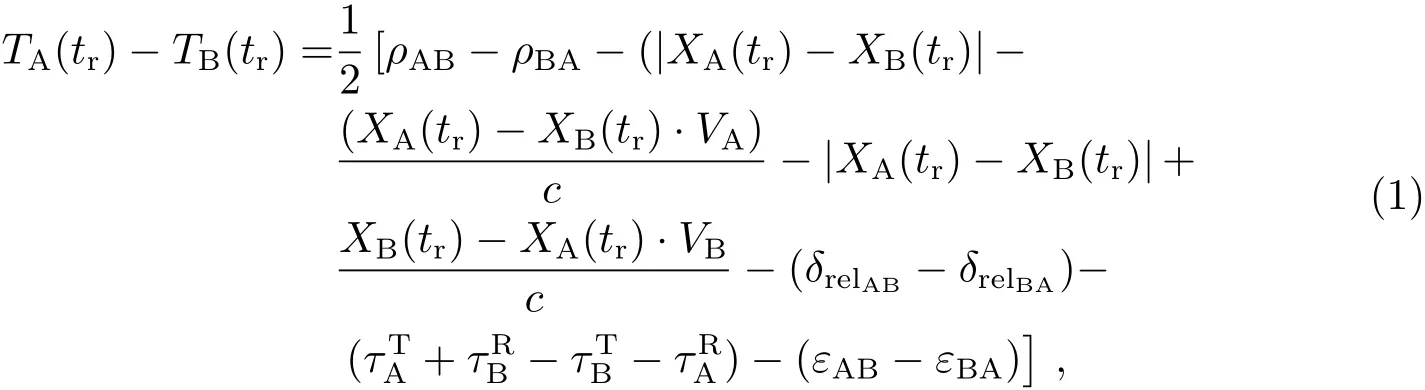
其中,tr为接收时刻、XA(tr)为A星的接收时刻、XB(tr)为B星的接收时刻,ρAB为A星发射、B星接收时的伪距;ρBA为B星发射、A星接收时的伪距;TA(tr)为A星在tr时刻的钟差;TB(tr)为B星在tr时刻的钟差;δrelAB为A星发射、B星接收时的相对论效应;δrelBA为B星发射、A星接收时的相对论效应;分别为B星发射端和接收端时延;分别为A星发射端和接收端时延;εBA和εAB分别为B星发射、A星接收和A星发射、B星接收的随机噪声,c为光速.修正各项误差后通过观测方程(1)解算星间钟差.

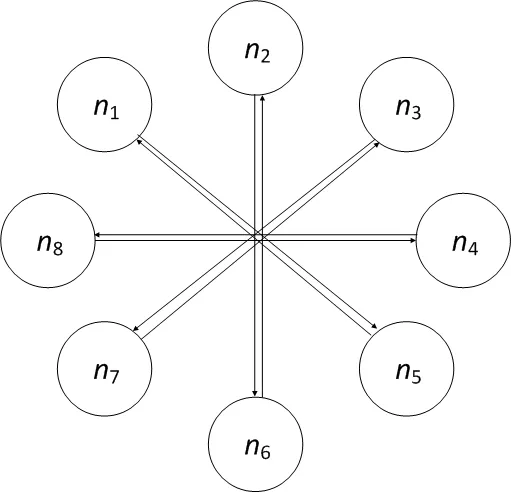
图2 分布模式拓扑结构图Fig.2 Topology structure of distributed model

4 系统时间算法对星上自主系统时间性能影响

系统时间的目的是通过不同的算法抑制原子钟的主要噪声,综合得到相对于单台原子钟更加稳定可靠的时间参考.星座自主导航时,与地面站失去联系,无法溯源到UTC(Coordinated Universal Time),只能通过精确建立系统时间的数学模型得到稳定度更好的时间序列.本文主要研究在集中计算模式下,采用加权平均算法建立星上自主系统时间数学模型,并分析模型中的各因素对于星上自主系统时间性能的影响从而选出最佳参数.

4.1 星上自主系统时间计算模型

星间观测值解出的钟差数据clock(i,t)和clock(j,t)为相对钟差(其中i、j为钟的编号),是所有星载钟相对主钟的钟差,为此首先需要采用等权的方式建立一个初始的参考时间系统,并将各星载钟的钟差归算到该参考时下[8−9],初始参考时间TA1(t)可按下式建立:

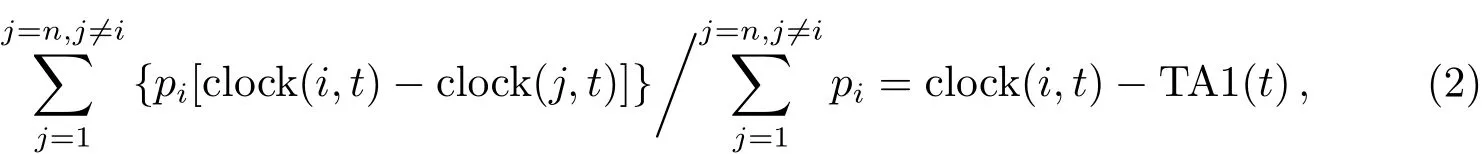
其中,pi为各钟权重,n为钟的数量.每台钟相对初始参考时间的钟差可由下式得到:

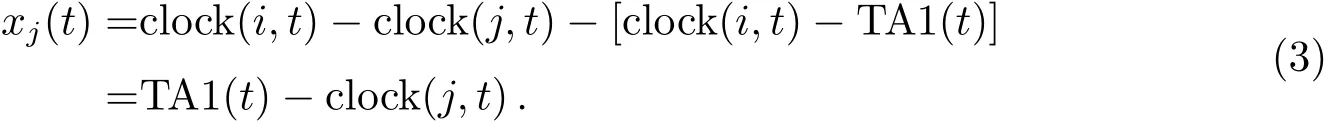
至此,由星间观测值解出的相对主钟的钟差就转化为相对某个系统时间的钟差,解决了有n台钟参与计算却有n−1列钟差数据的问题.导航星座中计算系统时间的星载钟绝大多数为铷钟,需要先扣除漂移才能进行计算.利用数列xj(t)分别拟合出每台钟的速率vj.

利用(4)式扣除各钟的钟速.加权方法虽然一直改进,但基本原理没有改变,都是用阿伦方差评定各钟的稳定度从而确定出每台钟的权重,方法如下:

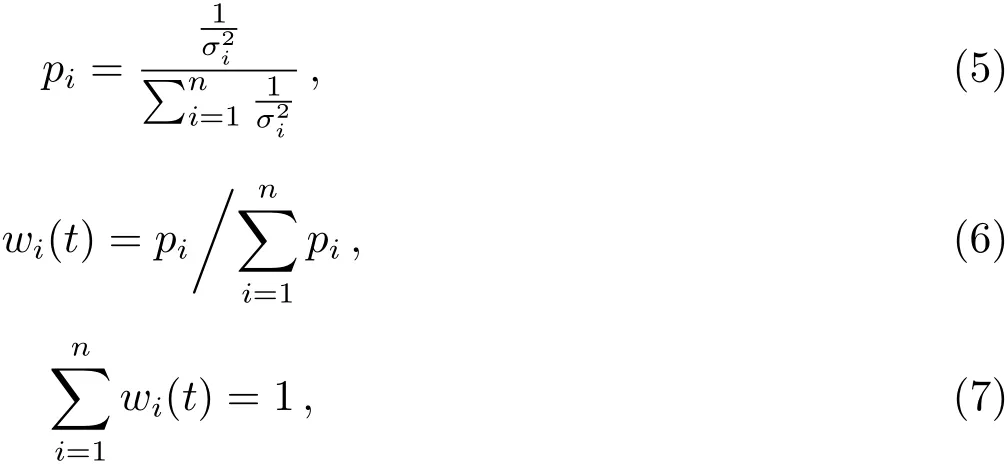
其中,σi为指钟标号,wi(t)为各钟的归一化权重,(5)式根据各钟的稳定度确定权重,(6)式和(7)式进行各钟权重的归一化处理.性能优良的钟稳定度较好,计算中所占权重较大,对于系统时间的影响也较大.当性能优良的钟出现故障时,严重影响系统时间的稳定性和连续性.需要找到一种合理的方式对权重进行约束,采用权上限的原则是为了限制性能好的钟的权重无限增加的反馈效应发生,降低好钟对于最终结果的影响.最大权公式为:

式中A为经验常数,目前星载钟的权上限选取原则还没有成熟的结论,仍然依据地面钟权上限选取原则进行判定,经验常数A采用法国权度局BIPM(Bureau International des Poidset Measures)规定的2.5,权重超限后必须重新归一化.在建立初始时间参考的基础上,由(2)–(9)式开始迭代计算TA1(t)−TA2(t):

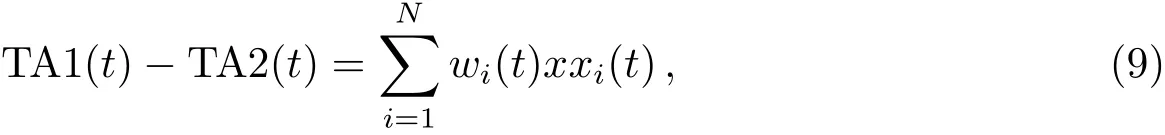
其中,TA2(t)为最终的星上纸面时间,也就是星上系统时间.至此,在新的系统时间下每台钟的钟差由下式得到:

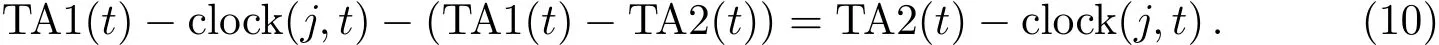
建立系统时间最终的目的是要服务用户,建立精确的星载钟预报模型,得到钟差、钟速和钟漂3参数,进而更新导航电文.PRN6、PRN18和PRN28这3颗卫星在计算期间星载钟发生切换造成数据无法使用,因此共有27台星载钟参与计算,其中PRN24和PRN26是铯钟,其他都是铷钟.由以上各式可以看到,数据插值方法、数据长度、更新频度和取权方式是影响星上系统时间性能的主要因素,因此我们将从这4个方面分析比较初始系统时间的偏差和稳定度[10−11].

4.2 数据插值方法对星上自主系统时间性能影响

卫星存在的不可见弧段将导致星间观测值解算的相对钟差是非连续不等间隔的序列,如图3所示.对于在固定采样时间的非等间隔数据,比如卫星双向测量数据的采样时间一般为每周一、周三和周五,可采用平均的方法来计算采样间隔.星间钟差的时间间隔带有一定的随机性,不能采用平均采样间隔方法处理,只能进行插值.因此选择合适的数据插值方法显得尤为重要.插值阶数越高,越容易产生病态结果,三次样条插值能避免此问题,分段三次Hermite插值是Lagrange插值的推广,同时利用函数信息和导数信息,保证插值函数能更好地密合原来的函数.

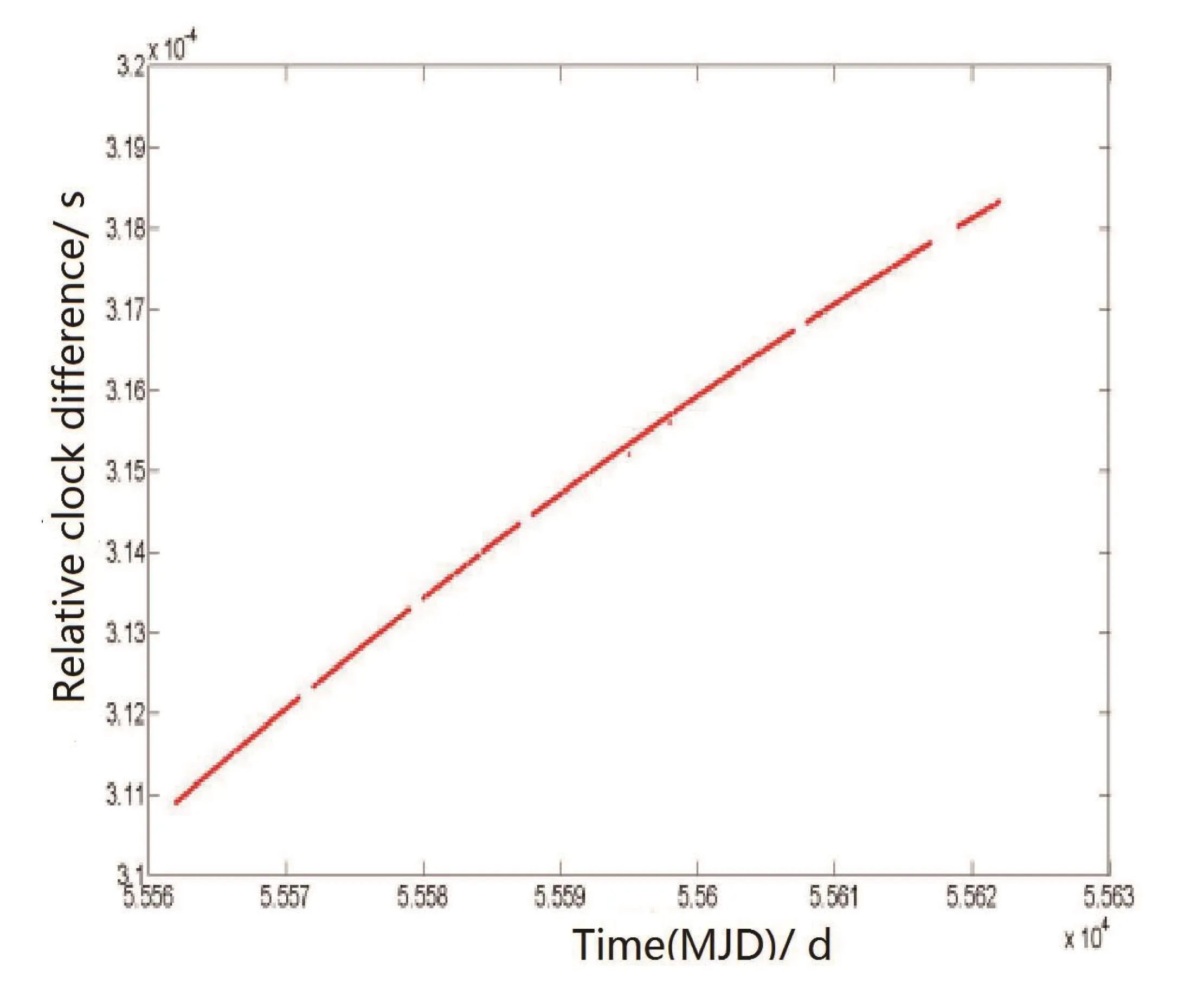
图3 星间观测值解算的星间钟差Fig.3 Clock difference obtained by inter-satellite observations

为了研究数据插值方法对星上系统时间性能的影响,论文分别比较了三次样条插值法(图示为spline法)和分段三次Hermite插值法(图示为pchip法)利用不同数据长度建立系统时间的性能.在更新频度和取权方式相同的情况下,比较数据长度6 h、8 h和12 h建立的系统时间偏差及稳定度.

4.2.1 数据长度为6 h的星上自主系统时间性能比较

如图4所示,采用分段三次Hermite法插值建立的星上自主系统时间60 d后时间偏差为111.5 ns,采用三次样条法插值建立的星上自主系统时间60 d后时间偏差为134 ns.

如图5所示,采用分段三次Hermite法插值建立的系统时间,天稳为1.56×10−14,5天稳为9.66×10−15,10天稳为3.53×10−15;采用三次样条法插值建立的系统时间天稳为4.63×10−14,5天稳为2.39×10−14,10天稳为1.50×10−14.

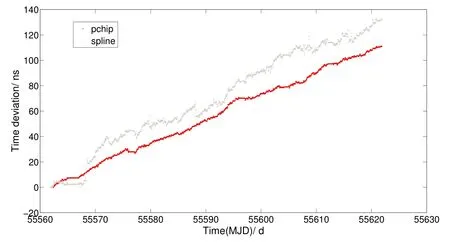
图4 数据长度为6 h建立的系统时间偏差Fig.4 System time bias with 6 h data length

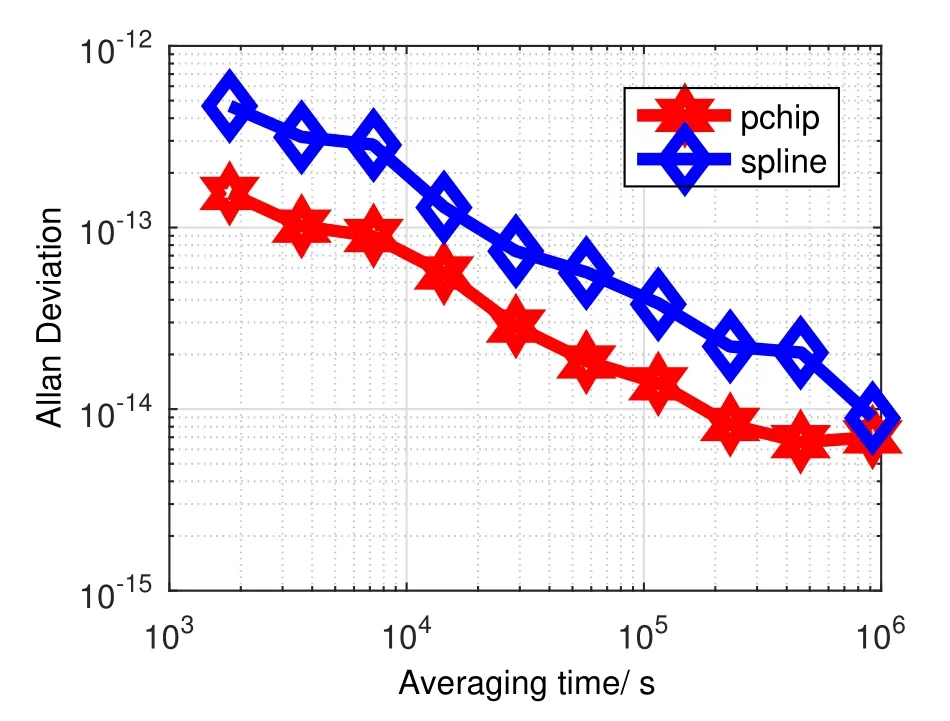
图5 数据长度为6 h建立的系统时间稳定度Fig.5 System time stability with 6 h data length

4.2.2 数据长度为8 h的星上自主系统时间性能比较

如图6所示,采用分段三次Hermite法插值建立的星上自主系统时间60 d后时间偏差为124.8 ns,采用三次样条法插值建立的星上自主系统时间60 d后时间偏差为142.6 ns.

如图7所示,采用分段三次Hermite法插值建立的系统时间,天稳为1.43×10−14,5天稳为8.72×10−15,10天稳为3.46×10−15;采用三次样条法插值建立的星上自主系统时间天稳为4.41×10−14,5天稳为2.10×10−14,10天稳为9.99×10−15.

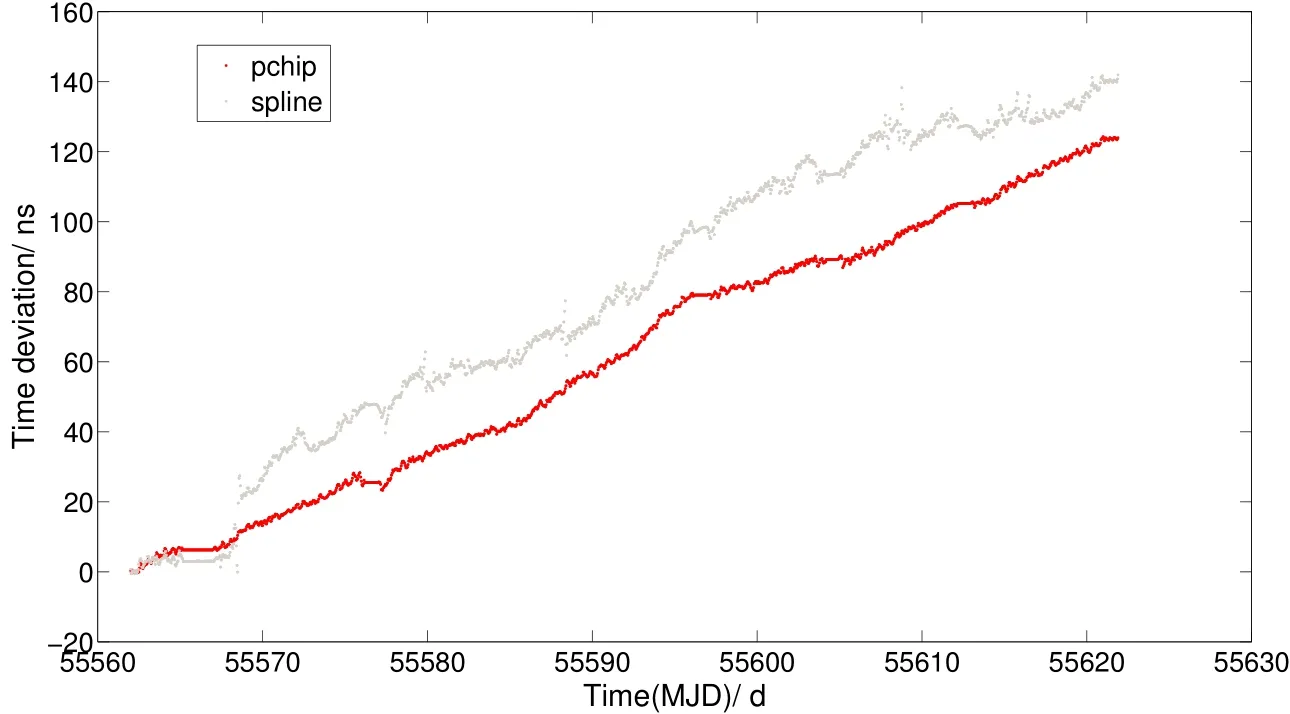
图6 数据长度为8 h建立的系统时间偏差Fig.6 System time bias with 8 h data length

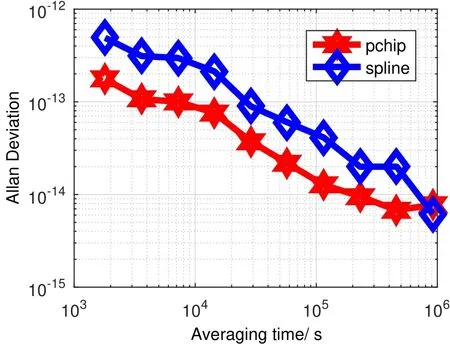
图7 数据长度为8 h建立的系统时间稳定度Fig.7 System time stability with 8 h data length

4.2.3 数据长度为12 h的星上自主系统时间性能比较

如图8所示,采用分段三次Hermite法插值建立的星上自主系统时间60 d后时间偏差为59.15 ns,采用三次样条法插值建立的星上自主系统时间60 d后时间偏差为71.87 ns.

如图9所示,采用分段三次Hermite法插值建立的系统时间,天稳为1.58×10−14,5天稳为5.75×10−15,10天稳为2.76×10−15;采用三次样条法插值建立的系统时间天稳为4.94×10−14,5天稳为1.77×10−14,10天稳为6.88×10−15.

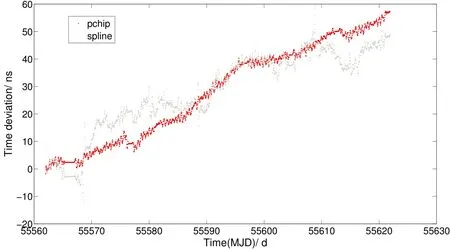
图8 数据长度为12 h建立的系统时间偏差Fig.8 System time bias with 12 h data length

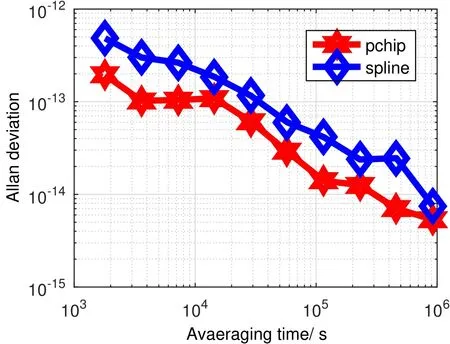
图9 数据长度为12 h建立的系统时间稳定度Fig.9 System time stability with 12 h data length

综上所述,采用相同的更新频度和不同的数据长度条件下,采用分段三次Hermite法插值建立的星上自主系统时间偏差较小且稳定度较好,由此可以说明分段三次Hermite法与三次样条法相比,对数据有较好的平滑作用,更适用于处理星间钟差数据.

4.3 数据长度对星上自主系统时间性能影响

数据长度的实质是利用多个长时段的数据计算星上自主系统时间,以数据窗口的方式实现,滑动更新窗口内的数据.数据长度的选取受限于主星的运算能力、主星的存储空间和链路的传输容量.滑动窗口的大小由数据长度决定,将前一数据段的末尾和后一数据段的初始位置进行相位拼接,实现相位微调,目的是为了得到一个更为平稳的纸面时间.具体的研究方法是在数据更新频度为1 h、采用1 h稳定度取权的条件下,采用加权平均算法利用长度为6 h、8 h、12 h、24 h和36 h的数据建立星上自主系统时间,给出系统时间偏差和系统时间稳定度比较分析.

如图10所示,在数据长度为6 h、8 h、12 h、24 h和36 h建立的星上自主系统时间经过60 d后时间偏差分别为111.5 ns、124.8 ns、59.15 ns、16.23 ns和20.71 ns,数据长度为24 h建立的星上自主系统时间偏差最小,总体上看,系统时间偏差随着数据长度的增加越来越小.

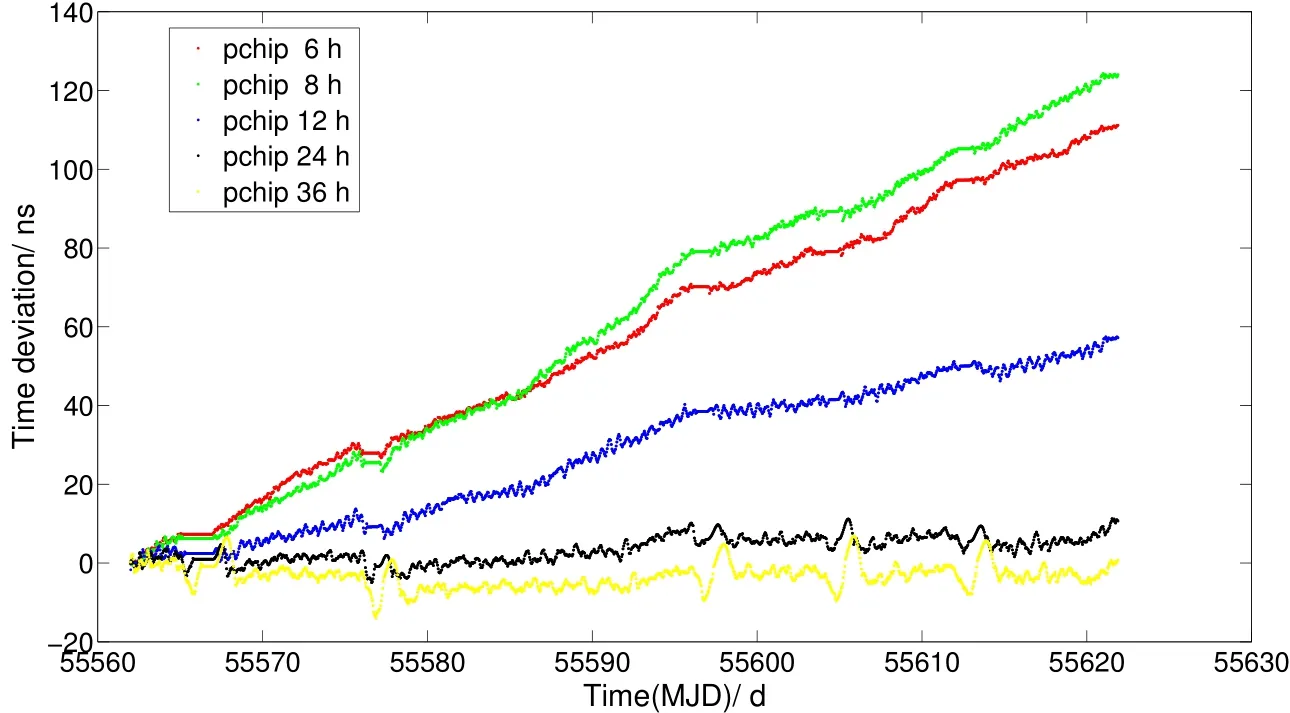
图10 不同数据长度建立的系统时间偏差Fig.10 System time bias with different data lengths

如图11所示,万秒稳以前不同数据长度建立的星上自主系统时间稳定度性能基本相当.万秒稳以后,数据长度越短建立的星上自主系统时间稳定度越好.综上所述,在相同的更新频度、取权方式和数据插值方法条件下,不同数据长度建立的星上自主系统时间偏差有较为明显的变化.时间偏差随着数据长度的增加越来越小,不同数据长度建立的星上自主系统时间稳定度性能基本相当,从长期稳定度性能来看,数据长度越长,星上自主系统时间稳定度性能越差.在计算星上自主系统时间时,数据长度越长,迭代次数相应增多,计算复杂度相应增大,对主星的计算能力要求越高;数据长度越长,数据量越大,占据主星内存越大,对主星的载荷要求越高;数据长度越长,对于链路传输的容量和速率的要求都相应增加.综合以上各方面因素以及系统时间偏差和稳定度情况,12 h的数据长度更适合于建立星上自主系统时间.

4.4 更新频度对星上自主系统时间性能影响

在星上自主系统时间计算中,在固定数据长度(即总的数据量不变)的情况下,更新频度与每小时数据量的乘积决定了更新数据量的大小.更新数据量的大小决定了进出滑动窗口的数据量的大小,也就是进入滑动窗口多少数据量,就要移出多少数据量.具体的研究方法是在数据长度为12 h,以1 h稳定度取权的条件下,针对更新频度分别为1 h、2 h和3 h采用加权平均算法计算星上自主系统时间,给出系统时间偏差和稳定度结果并进行比较分析.

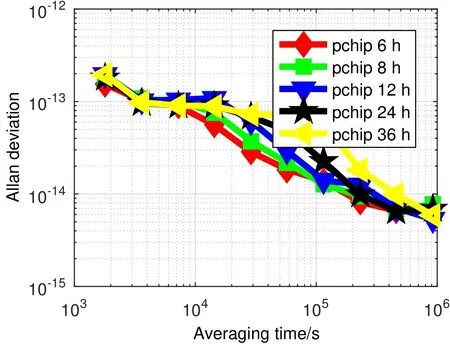
图11 不同数据长度建立的系统时间稳定度Fig.11 System time stability with different data lengths

如图12所示,更新频度1 h、2 h和3 h建立的星上自主系统时间60 d后时间偏差分别为59.15 ns、67.45 ns和61.9 ns.不同更新频度建立的星上自主系统时间稳定度如图13所示.

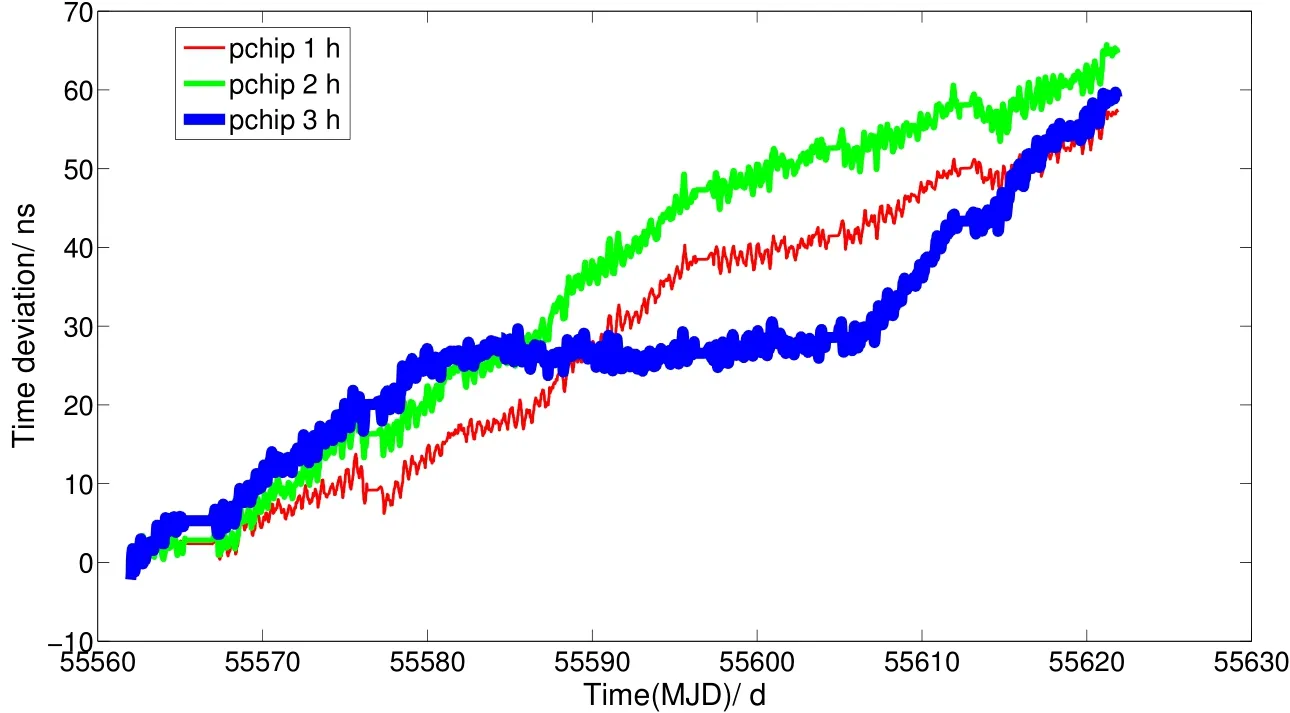
图12 不同更新频度建立的系统时间偏差Fig.12 System time bias with different update frequencies

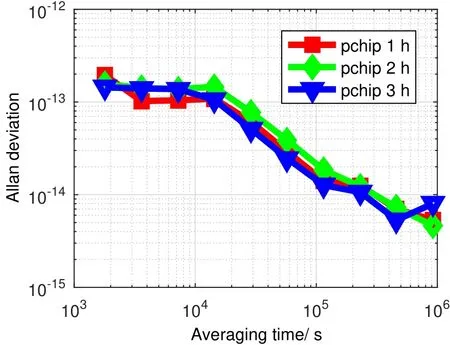
图13 不同更新频度建立的系统时间稳定度Fig.13 System time stability with different update frequencies

4.5 取权方式对星上自主系统时间性能影响

系统时间算法是按优化时间稳定度的思想来设计的,每个原子钟按照频率稳定度优劣加权.建立星上自主系统时间的目的是希望得到较为稳定的短期稳定度.通常情况下,系统时间的稳定度优于每一台钟的稳定度.具体的研究方法是:数据长度为12 h,更新频度为1 h,分别以1 h、2 h和3 h稳定度取权,采用加权平均算法计算星上自主系统时间,给出系统时间偏差和稳定度结果并进行比较分析.

如图14所示,分别以1 h、2 h和3 h稳定度取权建立的星上自主系统时间60 d后时间偏差分别为59.15 ns、47.91 ns和34.9 ns,3 h稳定度取权建立的星上自主系统时间偏差较小.

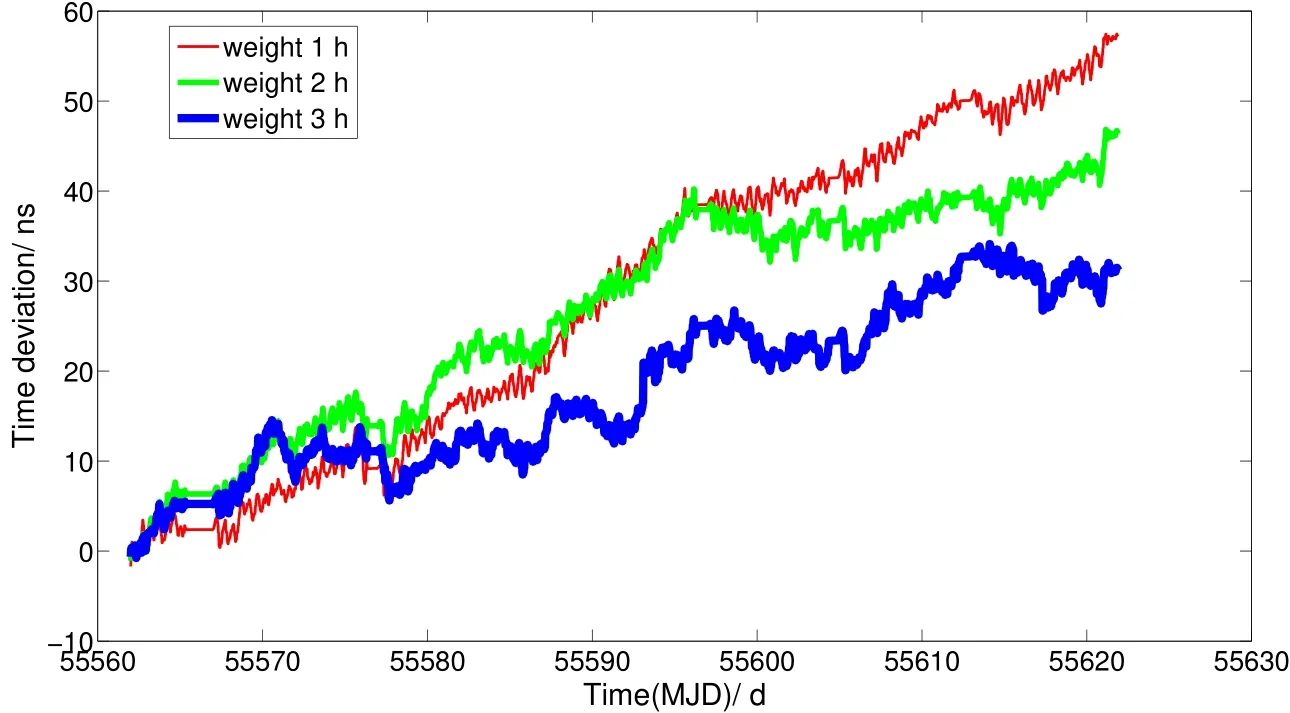
图14 不同取权方式建立的系统时间偏差Fig.14 System time bias with different weighting solutions

如图15所示,以1 h稳定度取权建立的星上自主系统时间,天稳为1.58×10−14,5天稳为5.75×10−15,10天稳为2.76×10−15;以2 h稳定度取权建立的星上自主系统时间,天稳为1.75×10−14,5天稳为9.32×10−15,10天稳为2.48×10−15;以3 h稳定度取权建立的星上自主系统时间,天稳为2.37×10−14,5天稳为1.13×10−14,10天稳为4.70×10−15.3种取权方式建立的星上自主系统时间的稳定度几乎相同,以1 h稳定度取权建立的星上自主系统时间稳定度整体较好.

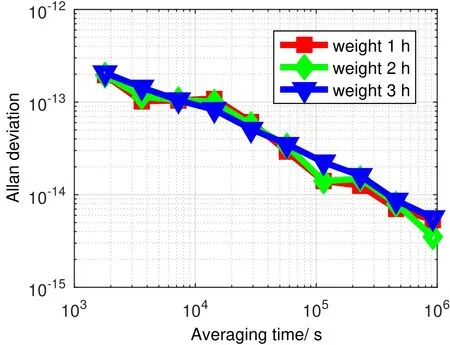
图15 不同取权方式建立的系统时间稳定度Fig.15 System time stability with different weighting solutions

5 结论

本文在利用GPS数据仿真星间伪距解算星间钟差的基础上,推导了星上系统时间的计算模型,研究了模型中的4个重要参数对于系统时间偏差和稳定度的影响.结果表明:在相同的数据长度、更新频度和数据插值方法下,以1 h稳定度取权建立的星上自主系统时间稳定度整体较好,但系统时间偏差性能略差,以3 h稳定度取权建立的星上自主系统时间偏差性能较好,但中长期稳定度略差.综合考虑,星上自主系统时间对中长期稳定度要求更高,因此选择相对较短的稳定度取权方式(如以1 h稳定度取权)更利于星上自主系统时间性能的提升.

[1]Kristine P,Paul A,John L.Proceedings of IEEE Aerospace Conference,2003:1589

[2]吴海涛,李孝辉,卢晓春,等.卫星导航系统时间基础.北京:科学出版社,2011:35-37

[3]米红,谢军,宋志强,等.导航定位学报,2014,2:1

[4]宋小勇.COMPASS导航卫星定轨研究.西安:长安大学,2009

[5]Altamimi Z,Collilieux X.Preliminary Analysis in View of the ITRF 2005.International Association of Geodesy Symposia,Berlin,August 22–26,2005

[6]朱俊.基于星间链路的导航卫星轨道确定及时间同步方法研究.长沙:国防科技大学,2011

[7]帅平,曲广吉.宇航学报,2005,26:768

[8]袁海波.原子钟噪声数字化模拟与钟速动态预测模型研究.北京:中国科学院研究生院,2009

[9]董绍武.守时中的若干重要技术问题研究.北京:中国科学院研究生院,2007

[10]Deimos J D.Clock Errors in Simulation and Characterisation.ION GNSS 19th International Technical Meeting of the Satellite Division,Texas,September 26–29,2006:815

[11]Riley W J.Methodologies for Time&Frequency Stability Measurement and Analysis.Hamilton Technical Services,Beaufort:WRILEY,2002