在数学活动中渗透分类思想的价值与策略

摘 要：分类，作为一种基本的数学思想或数学思维方法，在数学活动中有提供数学化的基础、简化思维的可能路径、丰富学生的组织策略的价值。文章以“图形的认识”教学为例，探讨了在数学活动中渗透分类思想时应注意分类探索新知需紧扣标准，分类解决问题时需迁移经验，分类表达关系时需重视多元。

关键词：数学活动；分类思想；价值；策略

作者简介：赵琴，江苏省扬州市育才小学东区校教师。（江苏 扬州 225000）

中图分类号：G623.5 文献标识码：A 文章编号：1671-0568（2018）34-0018-03

数学思想是人类对数学及其研究对象，对数学知识以及数学方法的本质性的认识，是在数学的发展史上形成和发展的。它与具体的知识技能相比，具有潜隐性，如“分类”“一一对应”“转化”“模型化”一些基本的数学思想方法贯穿于整个小学数学教学中，却并未作为一个知识点专门教学，而是隐藏在学生的认知活动中，逐步渗透，直至学生感悟并能自觉运用。史宁中教授指出，在认识图形的教学中，重要的是让学生学会对图形分类。本文以“图形的认识”教学为例，探讨如何在数学活动中深化学生的分类思想，感悟数学的理性思维。

一、数学活动中分类的价值

数学中的分类思想是指根据数学对象本质属性的相同点与不同点，将其分成不同种类的数学思想，是根据一定标准，对事物进行有序划分和组织的过程。分类，作为一种基本的数学思想或数学思维方法，在数学活动中对促进学生思维发展、认知发展、提升数学素养有着重要的作用。同时，分类也可被看成一种基本的数学活动。

1. 提供数学化的基础。弗赖登塔尔认为，学生的学习活动，与其说是学习数学，倒不如说是学习“数学化”。数学化分为水平数学化和垂直数学化两个层次。水平数学化是指由现实问题到数学问题的转化，是从“生活”到“符号”的转化。垂直数学化是从具体问题到抽象概念的转化，是从“符号”到“概念”的转化。分类活动中，需要学生对研究事物进行分析、比较，关注相同点与不同点，抽象出事物的一般特点与本质属性，建立概念。分类，作为数学化的前奏，为学生顺利进行数学化提供了必要的研究基础。

2. 简化思维的可能路径。分类具有明确的目的性，一是归类，二是区分类别，建立清晰的序。面对复杂的事物和现象时，归类与区分类别都可以梳理复杂的现象，有序、有层次地呈现多种可能路径，简化问题的解决路径，突出关键要素，让学生在可能路径中有条理地确定思路、优化思路，逐渐推进问题的解决，接近概念的本质。

3. 丰富学生的组织策略。组织策略是整合所学新知识之间、新旧知识之间的内在联系，形成新的知识结构的策略。在学习分类的过程中，学生可以逐步清晰概念的外延与内涵，也可以应用分类整理已有的知识网络，深度加工已有经验，完善已有认知结构。更为重要的是，学生可以将分类的方法迁移到其他学科的学习中去，潜移默化中受分类思想的影响，运用分类学习或解决生活中其他类似的问题。分类的经历，帮助学生丰富问题解决的组织策略，助推学生能力的增强。

二、数学活动中渗透分类思想的策略

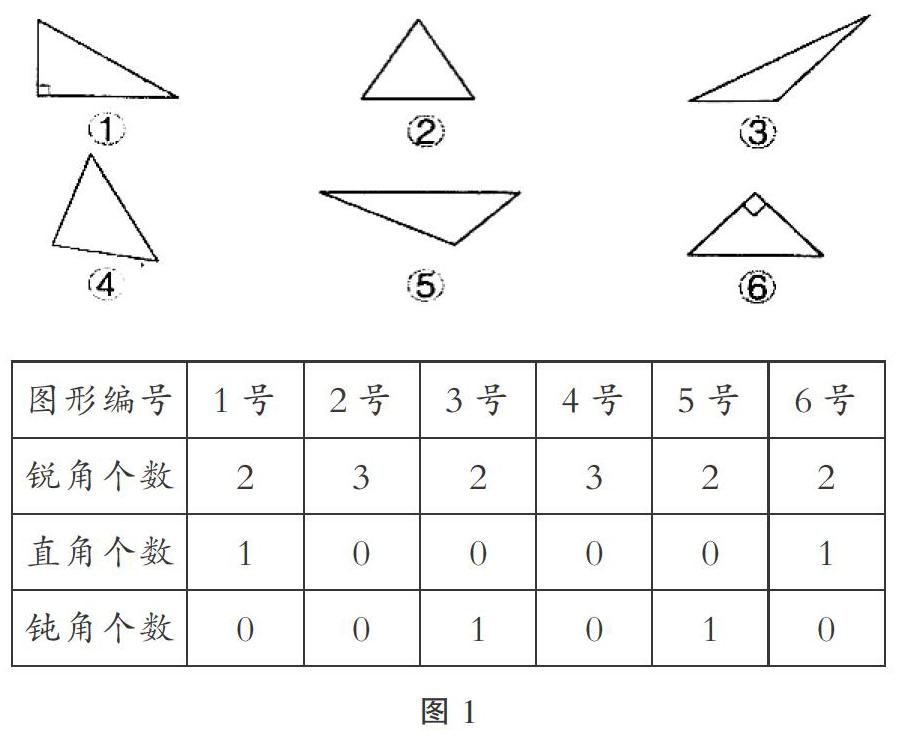
1. 分类探索新知，紧扣标准。在小学一年级会单独安排课时教学分类，要求学生掌握分类时做到不重复不遗漏，理解不同的分类标准分得的结果会不相同。在后续的学习中，分类依然存在于各种活动中，但分类标准逐渐淡化。如《三角形的分類》教学中，教师会出示多种三角形（如图1）让学生分类，并填入设计好的表格中，然后观察角的特点，形成共识：①和⑥一类，②和④一类，③和⑤一类，因为①和⑥都有一个直角，②和④都有三个锐角，③和⑤都有一个钝角。在此基础上，教师进行总结，像①和⑥这样的三角形叫作直角三角形，像②和④这样的三角形叫作锐角三角形，像③和⑤这样的三角形叫作钝角三角形。再观察所填表格中锐角的个数，确定每个三角形至少有两个锐角。

这是《三角形的分类》教学中常见的设计，学生对三角形内角的情况进行记录再分类，过程中学生并不清晰分类标准是什么。教师需要引导学生观察表格，在都有锐角的情况下还有什么不同，确定最大角为分类的标准。当清晰分类的标准与最大角有关时，三角形中至少有两个锐角就容易理解了，无需记忆和分辨。紧扣标准进行分类，不仅可以全面地考虑问题，也可深入理解概念的本质。分类是活动中的一部分，紧扣分类标准，可以帮助学生逐渐学会制定分类标准，并遵循标准分类，聚焦关键问题，做到不重复、不遗漏，形成清晰的认知结构。

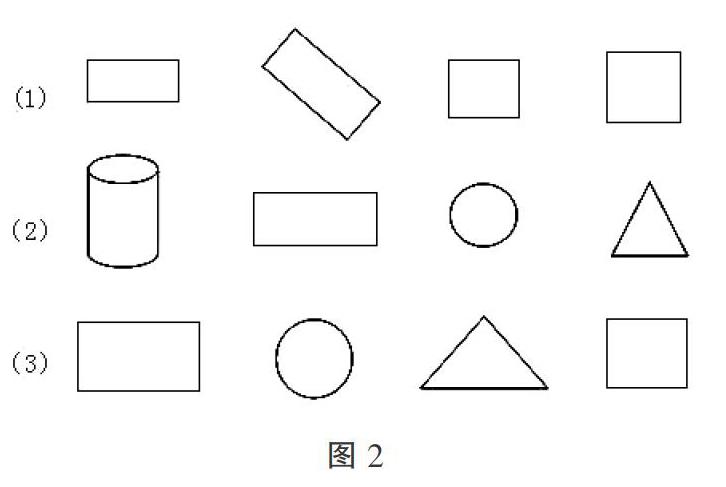
2. 分类解决问题，迁移经验。迁移是指一种学习对另一种学习的影响，或习得的经验对完成其他活动的影响。数学学习具有螺旋上升的特点，其中蕴含着如何发挥分类经验的迁移。首先，关注分类经验的积累。教学中，学生的分类训练可以从质性分类逐步走向量性分类、从局部找不同到整体分类，不同层次要求的分类可以帮助学生拓展分类的角度，获取分类的经验。如在一年级图形的认识中，可以让学生找出图2中哪个图形与其他三种不一样，找的过程就是训练学生分析图形特征的过程。其次，关注横向迁移和纵向迁移。横向迁移指先行学习内容与后继学习内容在难度、复杂程度和概括层次上属于同一水平的学习活动之间产生的影响。纵向迁移指先行学习内容与后续学习内容是不同水平的学习活动之间产生的影响。在图形的认识中，有些分类的教学是相通的。如在研究长方形和正方形的特征后，引导学生分析正方形具有长方形所有的特征，所以正方形是特殊的长方形。在学习长方体和正方体时，可以将已有的分类经验进行迁移，正方体具有长方体所有的特征，正方体是特殊的长方体。

分类思想的渗透，分类经验的迁移可以帮助学生理清数学问题，概括并总结有规律性的数学问题，寻求解题的策略，提高学生数学思维的条理性。

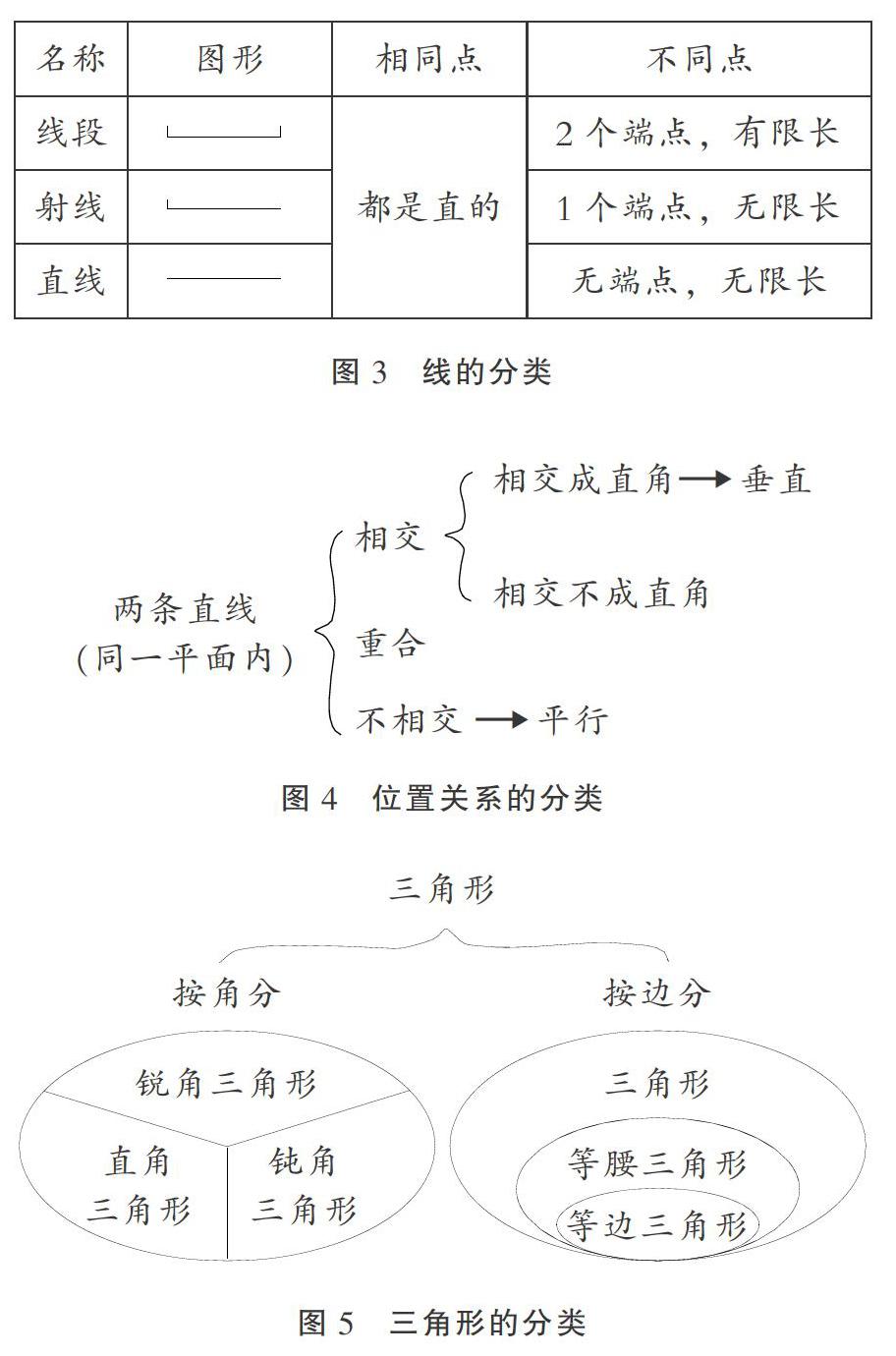
3. 分类表达关系，重视多元。数学是研究关系的一门学科，分类表达关系，可以帮助学生形成良好的认知结构，接近数学的本质。表达关系有多种形式，一般有表格式（图3）、树状式（图4）、韦恩图（图5）；表格式一般将图形特征进行对比，描述具体，对比鲜明；树状式一般表示图形之间的层次关系；韦恩图一般表示集合和图形关系。在实际运用中，只需根据学生理解的需要进行选择。

在分类表达关系时，教师要保持开放的心态，鼓励学生用多种方式自主表达，展现其对图形本质的理解。

4. 分类整理知识，优化思路。在“图形的认识”教学中，学生需根据图形的特征或相互间的关系进行分类整理，借助比较、对比、举例等方法来突出图形间的联系与区别。如立体图形可以按面是否是曲面进行分类，长方体与正方体为一类，圆柱与圆锥为一类；也可以按是否是直柱体分类，长方体、正方体和圆柱为一类，圆锥为一类。两种分类都可以开展研究，但从知识的化归角度分析，按是否是直柱体分类，研究图形体积的计算公式时，可以发现侧面积的计算公式是相通的，也可以归纳出直柱体的体积计算公式，底面积乘高等于体积，从而利于呈现数学内部的和谐。

数学知识是一个有机整体，各个知识点之间存在包含、并列等关系，复习时可以将平时所学的孤立的、分散的知识作横向、纵向或不同角度的分类，进行有序的整理，使其系统化，连成片，结成网，以便学生理解、记忆和应用。教师应引导学生按一定的标准把有关知识进行整理、分类、综合，并针对学生的整理情况，帮助学生优化分类的思路，完善知识结构，形成知识网络。

分类作为数学思想方法，其在教学中的运用还需遵循渗透性、反复性、明确性和实践性的教学原理。分类的价值需在学生亲历的活动中体悟，让学生进行实践、探索，积累分类的经验，感悟分类的需要，形成对分类的个体感悟，领悟分类思想的价值所在，逐渐形成面对问题时能自觉分类的意识。

参考文献：

[1] 史宁中.基本概念与运算法则[M].北京：高等教育出版社，2013.

责任编辑 黄 晶