POLYFLOW在设计氨纶高黏干法纺喷丝板中的运用

陈 斌，陈 桃，梁 燕

（1. 江苏奥神新材料股份有限公司，江苏连云港 222023;2. 江苏省高性能纤维产品质量监督中心，江苏连云港 222047）

氨纶纤维的高黏度纺是新兴的纺丝方式。目前，氨纶的纺丝原液的黏度相对较低，而干法纺的喷丝板对于纤维截面成型，以及是否具备可纺性起到决定性的作用。因此，设计出氨纶纤维的高粘度纺喷丝板至关重要。传统的设计方法一般采用理论计算法和实验法[1-3]。其中，理论计算法往往需要进行抽象和简化计算对象，得出理论解，对于高黏性聚合物很难使用解析法。而实验法往往受到多种因素限制，如流场扰动、加工粗糙度、人身安全等，存在资金投入大、研究周期长等缺点。采用POLYFLOW商业软件进行数值模拟能够解决前面两种方法的问题，在计算机上进行一次特定的模拟计算，与做实验没有什么区别。此外，数值模拟可以形象地使用流线图、云图等再现流动情景。POLYFLOW软件特别适合模拟高黏聚合物流动问题，在模拟黏性流动方面始终处于领先地位，本课题将采用理论计算法及POLYFLOW软件数值模拟法进行氨纶纤维的高粘度干法纺喷丝板的设计。

1 材质选型

氨纶纤维的原液中含有大量的DMAC，而DMAC有一定的腐蚀性，喷丝板的材质必须具备耐腐蚀性及耐磨性，常用的材质为SUS304及SUS316，SUS316耐磨蚀性优于SUS304。因此，材质选为SUS316。

2 导孔的形状设计

喷丝板的导孔与微孔的连接处是否流畅，将决定溶液是否出现滞留现象，所以圆锥角θ角（图1）即微孔的入口角，决定溶液的流动状态是否平稳，合理的θ角可使溶液的流动收敛性更加缓和，喷丝板的导孔直径选为2.5mm，圆锥角θ角初步设计为60°、90°、120°、180°，依据POLYFLOW进行流场分析。

氨纶纤维原液的黏度约为600Pa.s，属于假塑性非牛顿流体，高黏性聚合物,其流动特性为非线性，根据流动特性选用黏性流动方程Bird-carreau law。

2.1 三维建模及网格化

首先，我们用CAD对θ角为60°、90°、120°、180°的喷丝板进行三维建模，然后进行以下操作：把保存好的模型导入到Ansys polyflow软件中，进行网格(mesh)划分（图1），并设定边界为入口、出口、壁面。

图1 θ角为60°喷丝板模型网格

2.2 polydata中参数设置

三维模型网格划分后，上传到Polydata中，首先创建一个新任务，选择稳态流动类型，在新任务下创建一个子任务，选择广义牛顿等温流动类型，子任务流体区域设置为整体导孔模型，材料数据设置为依赖剪切速率的黏度模型，根据聚合物特性，选取本结构方程（Bird-carreau law）。其中，剪切黏度（Modify fac）为600Pa.s，松弛时间（Modify tnat）为0.01s，剪切速率（Modify expom）为7 500（1/s）。边界条件设置：入口（inflow)设定体积流量0.01mL/s；出口（outlet)设定流向fn=fs=0；壁面（wall)设定受力方向vn=vs=0，把单位设置好，保存后导入到模块Solution中进行计算。

2.3 计算结果

图2为圆锥角θ角为60°、90°、120°、180°的喷丝板进行数值模拟的流场图。

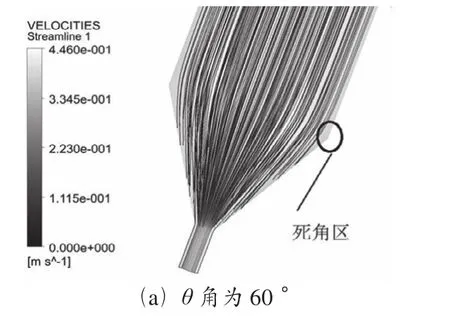
图2 导孔的θ角为不同角度的流场

在以上流场图中可以看出，随着θ角的角度增大，导孔内的死角区域就越来越大。导孔的θ角为60°时流场基本无死角。实验得出，θ角为60°较为合理。

3 孔径的设计

3.1 微孔直径的理论计算

微孔直径的计算公式为：

式中：do为微孔的直径(cm)；Q为单孔流量(cm3/s)，取值为：0.02，γ为理想孔的剪切速率(1/s)，剪切速率为6 000。

经过初步计算，do为0.32mm。经过理论计算，确定了孔径后，使用POLYFLOW软件分别对0.3mm、0.35mm、0.4mm的圆孔孔径进行数值模拟，确认氨纶溶液通过微孔的流场及剪切速率，进一步对比不同孔径的流场状态，最终确定微孔尺寸。

3.2 微孔数值模拟在POLYFLOW中设置

由以上的数值模拟可知，θ角取值为60°时流场非常顺畅，基本无死角，因此，导孔的θ角取为60°。分别对0.3mm、0.35mm、0.4mm的孔径的喷丝板进行建模并网格化。由于喷丝板的尺寸较小，一般工作站可以承担计算能力，完全可以使用三维建模及网格化，网格的最小尺寸为0.01mm。为保证模拟计算的准确性，在模型的出口处增设膨胀层，设定参数为过渡比率为0.1，层数为5，增长率为1.2，把保存好的模型分别导入到Ansys polyflow软件中，Polydata中的设置步骤同导孔模拟，如图3。

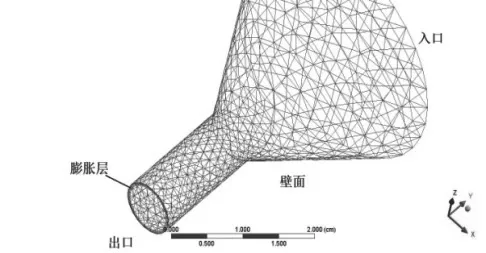
图3 孔径为0.3mm的微孔网格

3.3 不同孔径的模拟结果

图4 为不同孔径进行数值模拟流速等值线图，图5为不同孔径的剪切速率云图。

图4 不同孔径喷丝板微孔流速等值线图

根据图4模拟出来的不同孔径的喷丝板的流速等值线图可以看出：壁面的流速非常小，越靠近微孔中间，流速就越来越大，流速过快，聚合物在微孔中的松弛时间得不到保证，造成出口处的应力较集中，模拟得到的数值见表1。

图5 不同孔径喷丝板微孔剪切速率图

根据图5显示，孔径为0.3mm和0.35mm喷丝板的出口处剪切速率较高，分别达到18 270、9 500，过高的剪切速率使溶液通过微孔后产生破裂，纺丝时容易产生结点及滴原液现象，而孔径为0.4mm的喷丝板压力分布较均匀，微孔出口处剪切速率为6 700，聚合物通过微孔的流速较平稳，有利于提高纺丝的操作性能，所以，孔径可选为0.4mm。

表1 不同孔径的流速及压力值

3.3 微孔的长径比的设计

根据聚合物在微孔中的流动特性，临界剪切速率随着长径比增加而增大，有利于减少出口的膨大效应，在纺丝时有较好的操作性能。依据长径比的选择原则，聚合物在微孔的停留时间必须小于聚合物的松弛时间。现依据孔径为0.4mm的流场图可知[4,5]，溶液通过微孔的最大流速约为0.12m/s，氨纶溶液的松弛时间约为0.01s，通过计算可得出微孔长度L=1.2mm，微孔的长径比约为3，这样的长径比在加工及清洗中都不存在困难，经过取整可以得出微孔的长径比为3。

4 结语

本课题运用POLYFLOW软件针对氨纶高黏度干法纺喷丝板进行了模拟，分析了圆孔型喷丝板在不同导孔及不同孔径溶液流过的流场及剪切速率，得出以下结论：

（1）喷丝板的导孔圆锥角θ角在60°时，导孔与微孔连接处溶液流通死角较小，随着θ角增大，流通死角就越大，溶液存在滞留现象越严重。

（2）喷丝板的孔径为0.4mm时，微孔出口处的剪切速率适中，适合氨纶高黏度干法纺丝要求，溶液的流场速较为平稳，根据模拟的最高流速计算出微孔的长径比。

计算机数值模拟的运用缩短了喷丝板的研发周期，降低了成本，设计工作将更加方便和直观，设计的一次成功率也显著提高。