加筋圆柱壳开孔围栏肘板拓扑优化设计

宋晓飞，肖伟，何其健，刘均，程远胜

1华中科技大学船舶与海洋工程学院，湖北武汉430074

2中国舰船研究设计中心，湖北武汉430064

0 引 言

出于人员进出等原因，在耐压圆柱壳上必须设置开孔围栏，而开孔围栏的出现打断了环向肋骨的连续性，因而在开孔围栏与肋骨的连接处易出现应力集中。因此，需对开孔围栏与环向肋骨连接肘板进行优化设计，以降低连接处的局部应力集中程度。

张会新等［1］以船底板架和上层建筑板架为研究对象，探讨了结构拓扑与形状优化设计方法在船舶设计中的应用，对船底板架结构进行优化后，结构重量减少了15.82%。王波等［2］针对船体的梁连接节点，在ANSYS中建立连接节点的壳单元模型，探讨了肘板尺寸变化对节点承载能力的影响规律，并对比了几种常见节点的强度和屈曲性能。程远胜等［3］对船舶构件间的三角形连接肘板进行拓扑优化分析，提出了一种新的肘板结构型式，相对于传统的三角形肘板，新型肘板结构有效降低了节点应力集中程度。经过多年的研究，针对局部结构（如舱口形状、剖面结构等）的尺寸优化和形状优化已相当成功，而结构拓扑优化的进展则相对缓慢。目前，连续体拓扑优化理论已较为成熟，在汽车工业、航天工程等领域有着较广泛的应用［4］，在船舶行业亦有所应用。但有关实用化的船舶构件拓扑与形状优化设计案例还较少。本文将以开孔围栏和环向肋骨连接肘板结构为研究对象进行拓扑优化研究，分别研究开孔围栏位置以及连接肘板和开孔围栏中心偏置时对肘板拓扑优化结果的影响，用以为类似的结构设计提供参考。

1 耐压圆柱壳开孔围栏与环向肋骨连接节点应力分析

1.1 整体模型应力计算

选取含正交开孔围栏的耐压加筋圆柱壳为研究对象，开孔围栏位于耐压圆柱壳正中，环向肋骨通过围栏中心，结构如图1所示。耐压圆柱壳全长L=8 m，直径Ø=6 m，肋距l=0.4 m，壳板厚24 mm；环向肋骨尺寸为；开孔围栏直径为660 mm，围栏高500 mm，围栏厚56 mm。结构材料弹性模量E=196 GPa，泊松比μ=0.3，材料密度ρ=7 800 kg/m3。

整体结构有限元模型全局坐标系为圆柱坐标系，坐标原点位于耐压圆柱壳左端圆心处，耐压圆柱壳的径向为X轴，周向角度为Y轴，轴向为Z轴。整体结构的有限元模型全部采用Shell 181单元模拟，共划分有114 483个单元。为模拟耐压圆柱壳的水下受力情况，在耐压圆柱壳左端约束其X，Y，Z方向的自由度，在其右端约束X，Y方向的自由度，然后在耐压圆柱壳（含围栏）外表面施加5 MPa的均布压力，并将轴向压力转化为相应的节点力施加在耐压圆柱壳右端的所有节点上。

1.2 子模型应力计算

1.2.1 有限元子模型

本文采用子模型的方法对肘板节点应力进行精细化分析。子模型法基于圣维南原理，以等效载荷代替实际分布载荷，并保证子模型切割边界避开载荷集中及应力集中位置，在子模型内部就可以得到较精确的应力解［5-6］。本文以围栏开孔为中心沿Z轴正负方向各3档肋距、沿Y轴正负方向各45°范围内的结构为子模型（图2），子模型的网格尺寸为15 mm。在进行边界切割、插值后，在子模型上施加相应的约束及载荷。经静力计算后，对比子模型边界的von Mises应力和整体模型在切割位置的von Mises应力，确认两者的应力趋势一致，若应力值比较接近，则认为子模型的边界选取较为合理。

1.2.2 有限元子模型强度计算结果分析

将有限元子模型导入商业软件Optistruct中进行强度计算，子模型的von Mises应力云图如图3所示。由应力云图可以发现，最大应力出现在环向肋骨与围栏连接处，为1 114 MPa。为了降低该处的应力集中程度，加宽了连接处肋骨的面板。根据舰船通用规范中对骨材尺寸的要求，肋骨面板宽度不超过板厚的8倍，同时为了保证自然过渡，长度不宜过小。本文肋骨面板加宽后的宽度取上限值160 mm，加宽区域的长度为宽度区域变化值的4倍，为424 mm。按照上述方法截取含加宽面板的子模型后，同样计算了其强度，整体von Mises应力云图如图4所示。因两侧加宽面板相同，取一侧加宽面板的von Mises应力云图如图5所示。

由图5可见，面板区域共有3个高应力节点：第1个位于加宽面板远离围栏一端，称为高应力节点1，应力值为962 MPa；第2个位于加宽面板与围栏连接处的侧边端点，称为高应力节点2，应力值为670 MPa；第3个位于加宽面板与围栏连接处的中点，称为高应力节点3，应力值为760 MPa。在之后的分析中，将以高应力节点1，2和3来区分各应力的位置。经对比发现，在加宽连接处的面板后，面板最大von Mises应力降低了152 MPa，约13.6%；且最大应力位置由连接处转移到了高应力节点1处，加宽面板起到了肘板的作用。下一步，将通过对加宽面板（即肘板）的拓扑优化进一步降低面板区域应力。

2 耐压圆柱壳开孔围栏与环向肋骨连接节点结构的拓扑优化

2.1 拓扑优化数学模型

本文基于有限元软件Optistruct进行连接节点拓扑优化，Optistruct拓扑优化的材料模式采用密度法（SIMP方法），即将有限元模型设计空间每个单元的“单元密度”作为设计变量。该“单元密度”同结构的材料参数有关（单元密度与材料弹性模量E之间具有某种函数关系），在0～1之间连续取值，优化求解后单元密度为1（或接近1）表示该单元位置处的材料很重要，需保留；优化求解后单元密度为0（或接近0）则表示该单元位置处的材料不重要，可以删除。通过控制单元的密度向0或者1两端收敛，得到了拓扑优化结果，经进一步工程化处理，可成为实用的结构。

本文的优化对象为图5所示的加宽的面板（即肘板），设计变量为肘板结构的单元密度。目标函数为面板及肘板区域最大应力的极小化；同时，约束肋骨腹板应力不超过600 MPa，围栏应力不超过750 MPa，肘板的体积分数不超过70%。

2.2 拓扑优化结果及工程化处理

求解上述数学模型，至优化迭代27步时停止计算。目标函数随迭代步数的变化历程曲线如图6所示。图中，横坐标为迭代步数，纵坐标为目标函数的数值。由图6可以看出，最后的目标函数已经收敛，说明肘板的优化在该数学模型下已经达到最优。为便于观察，截取了肘板（设计区域）单元和部分面板单元，收敛时的结构单元密度图如图7所示。

由图7可以发现，肘板长度并非为加宽区域的最大值，即肘板并非是沿肋骨越长越好。根据图7，取单元密度大于0.6的部分作为保留区域，其余部分删除；对保留区域进行工程化处理后得到与单元密度图中红色区域形状类似的肘板，肘板的总长度为317 mm，其中变宽度区域的长度为158 mm，并且两侧肘板相似，工程化处理后的肘板形状如图8所示。对工程化处理后的结构模型重新划分网格，并保持与优化前肘板相同的单元尺度。

对优化结构进行强度计算，得到结构的von Mises应力云图如图8所示，肘板及面板区域的von Mises应力云图如图9所示。与未优化时高应力节点的位置相似，优化后，结构的高应力节点1位于肘板远离围栏一端与面板连接处；高应力节点2位于加宽面板与围栏连接处的侧边端点；高应力节点3位于加宽面板与围栏连接处的中点。优化后，结构高应力节点1～3的应力值分别为887，617和703 MPa。进行肘板优化后，3个高应力节点的应力值均有所降低，其中高应力节点1下降最多，降低了75 MPa，约7.8%。加肘板前、后，优化前、后高应力节点的应力值如表1所示。由表中数值及应力云图可知，优化后的肘板及面板应力分布更加均衡，并且最大应力较无肘板方案降低了20.4%，而肘板未优化方案较无肘板方案仅降低了13.6%。

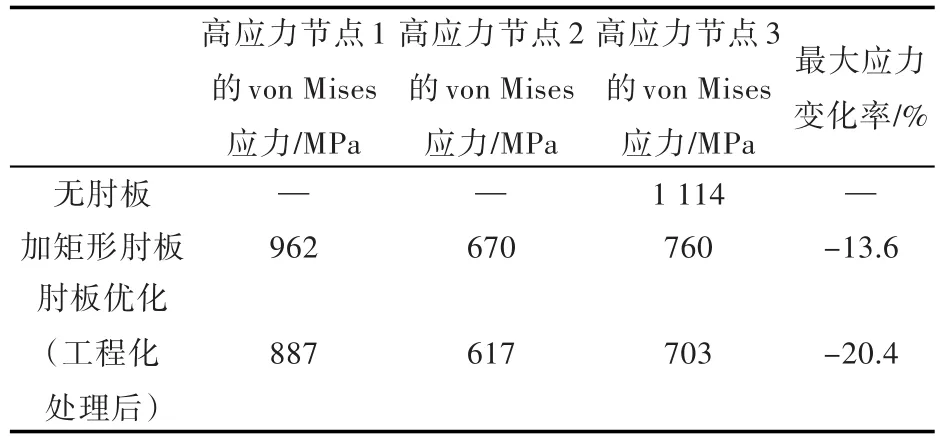
表1 耐压圆柱壳正交开孔围栏子模型各连接形式von Mises应力对比Table 1 Comparison of von Mises stress about different types of connective area of orthogonal opening fence sub-model

3 开孔围栏偏置对连接节点结构拓扑优化的影响

3.1 开孔围栏横向偏置拓扑优化

基于舱内设备布置的需要，常常需要对开孔围栏进行必要的横向/纵向偏置。本文根据设备布置情况选取了开孔围栏横向偏置距离800 mm，此时，两侧肋骨与围栏的连接位置不对称。按照上文所述方法截取子模型、添加切割边界并进行强度计算。横向偏置子模型强度计算的von Mises应力云图如图10所示。在肋骨与围栏连接处添加与上文相同尺寸的加宽面板（长424 mm，宽160 mm），对含加宽面板（即肘板）的子模型进行强度计算，肘板及面板的von Mises应力云图如图11所示。

不含肘板的横向偏置围栏结构的最大应力为998 MPa，出现在肋骨与围栏的连接处。添加矩形肘板后，3个高应力节点的应力值分别为894，670和696 MPa。与围栏不偏置的情况类似，添加肘板后，最大应力转移到肘板远离围栏一端、与面板连接处。

针对含肘板的结构，采用和上文相同的数学模型进行肘板区域拓扑优化。经过27步迭代后，优化计算收敛，最后一步迭代的肘板、面板单元密度图如图12所示。由图可知，当围栏横向偏置时，远离耐压圆柱壳中心一侧的肘板面积更大，而靠近耐压圆柱壳中心的肘板相对较小。

对拓扑优化结构进行工程化处理，并对得到的新结构进行强度计算。工程化处理后的肘板及肘板面板上的von Mises应力分布如图13所示。

拓扑优化后，高应力节点1，2，3的von Mises应力分别为914，608和640 MPa。无肘板、加肘板及肘板优化后的高应力节点的应力汇总如表2所示。对于开孔围栏横向偏置的结构，在面板处添加肘板可以有效降低肘板面板区域的应力。拓扑优化后的肘板，在工程化处理时，因删除了部分密度不为0的单元，导致优化后高应力节点1的应力略微上升（2.2%）；但其余高应力节点的应力值分别下降了62 MPa（9.2%）和235 MPa（33.7%）。

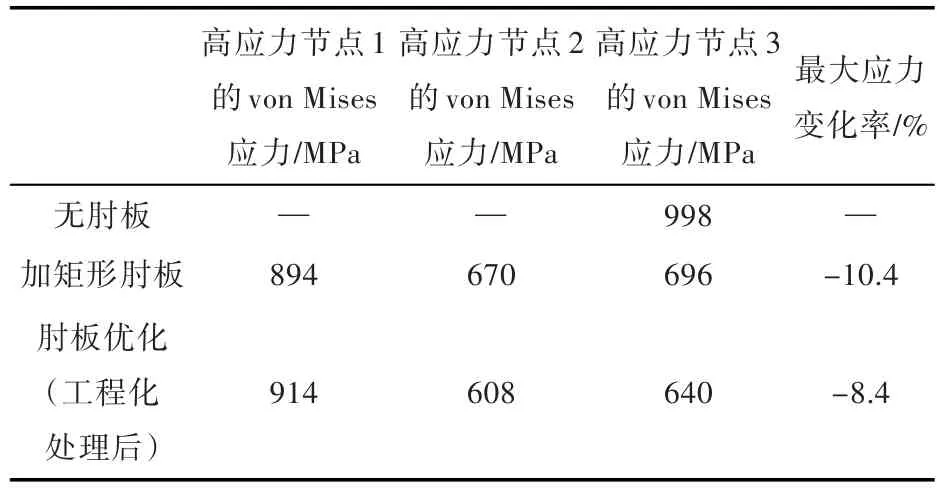
表2 耐压圆柱壳横向偏置开孔围栏各连接形式von Mises应力对比Table 2 Comparison of von Mises stress about different types of connective area of transverse offset fence

3.2 开孔围栏横向、纵向偏置拓扑优化

为了分析开孔围栏纵向偏置对拓扑优化结果的影响，在开孔围栏横向偏置的基础上，将开孔围栏进行了纵向偏置。在不切断相邻肋骨的前提下，参考文献［7］中取开孔围栏的纵向偏置距离为40 mm，此时两侧肋骨与围栏的连接位置不对称，并且环向肋骨不再通过围栏圆筒的中心。按照上文所述方法，肘板尺寸分别截取无肘板子模型、含肘板子模型并进行强度计算，不含肘板子模型的von Mises应力云图如图14所示，含肘板子模型的肘板和面板的von Mises应力云图如图15所示。

不含肘板的横向、纵向偏置围栏结构的最大von Mises应力为1 040 MPa，出现在肋骨与围栏的连接处。添加矩形肘板后，3个高应力节点的von Mises应力值分别为903，715和722 MPa。与围栏不偏置的情况类似，添加肘板后最大应力转移到了肘板远离围栏一端、与面板连接处。横向、纵向偏置围栏结构的耐压壳板的应力较高，因本文着重讨论肋骨面板及肘板的应力，故耐压壳的应力云图不再给出。

针对含肘板的结构，采用和上文相同的数学模型进行肘板区域拓扑优化。经过12步迭代后，优化计算收敛，最后一个迭代步的肘板、面板单元密度图如图16所示。肘板面积在围栏两侧的分布规律与仅横向偏置的情况类似，在远离围栏一侧较多，而肘板面积沿纵向关于面板中心线近似对称，并未出现明显的沿纵向的不对称，这可能与围栏沿纵向偏置距离较小有关。

对拓扑优化结构进行工程化处理，并对得到的新结构进行强度计算。工程化处理后的肘板及肘板面板上的von Mises应力分布如图17所示。

拓扑优化后，高应力节点1，2，3的von Mises应力分别为907，564和648 MPa。无肘板、加肘板及肘板优化后的高应力节点的应力汇总如表3所示。与开孔围栏横向偏置的结构类似，在面板处添加肘板可以有效降低肘板面板区域的应力，拓扑优化后的肘板在保证高应力节点1处的应力相当的情况下，明显改善了高应力节点2，3处的应力值，分别下降了151 MPa（21.1%）和74 MPa（10.2%）。

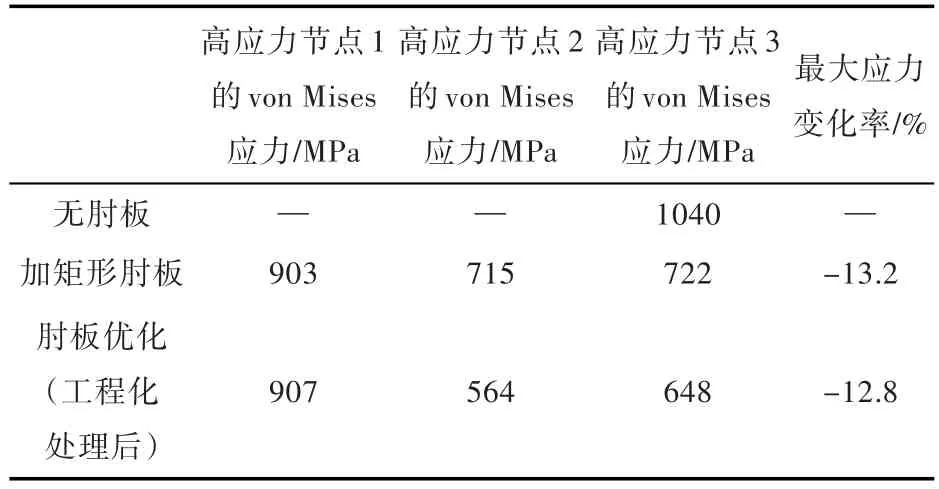
表3 耐压圆柱壳双向偏置开孔围栏各连接形式von Mises应力对比Table 3 Comparison of von Mises stress about different types of connective area of bi-offset fence

4 结 论

本文通过对开孔围栏与环向肋骨连接肘板进行拓扑优化，以及计算分析开孔围栏横向、纵向偏置对拓扑优化结果的影响，得出以下几点结论：

1）在正交开孔围栏圆柱壳结构中，开孔围栏与环向肋骨连接肘板经过优化可以有效降低连接处的应力集中程度，对于本文的案例，应力降低了约20%；肘板优化后应力值降低了7.7%。

2）在正交开孔围栏圆柱壳结构中，开孔围栏与环向肋骨连接肘板并非沿肋骨越长越好，其存在着一个对应应力最小的最优参数，该参数可通过求解连接肘板优化设计数学模型获得。

3）在本文的横向偏置开孔围栏圆柱壳结构中，开孔围栏与环向肋骨连接肘板较优的设计方案为在围栏两侧不对称，并且在远离耐压壳中心一侧面积较大。

4）当开孔围栏沿纵向偏置距离较小时，将开孔围栏与环向肋骨连接肘板设计成关于面板中心对称即可。

5）对于围栏偏置情况，进行了开孔围栏与环向肋骨连接肘板优化，在保证高应力节点最大值相当的情况下，进一步降低了其他高应力节点的应力水平。

［1］张会新，杨德庆.典型船舶板架拓扑与形状优化设计［J］.中国舰船研究，2015，10（6）：27-33，59.ZHANG H X，YANG D Q.Typical shape and topology optimization design of the ship grillage structure［J］.Chinese Journal of Ship Research，2015，10（6）：27-33，59（in Chinese）.

［2］王波，杨平.船舶结构节点的承载力分析［J］.船海工程，2010，39（2）：18-21.WANG B，YANG P.Analysis of the load bearing capacity of ship structural details［J］.Ship&Ocean Engineering，2010，39（2）：18-21（in Chinese）.

［3］程远胜，刘甜甜，刘均.船舶肘板拓扑优化设计［J］.中国舰船研究，2015，10（5）：53-58，70.CHENG Y S，LIU T T，LIU J.Topology optimization of ship bracket structures［J］.Chinese Journal of Ship Research，2015，10（5）：53-58，70（in Chinese）.

［4］夏天翔，姚卫星.连续体结构拓扑优化方法评述［J］.航空工程进展，2011，2（1）：1-11，55.XIA T X，YAO W X.A survey of topology optimization of continuum structure［J］.Advancesin Aeronautical Science and Engineering，2011，2（1）：1-11，55（in Chinese）.

［5］BENDSØE M P，SIGMUND O.Topology optimization：theory，methods，and applications［M］.2nd ed.Berlin：Springer，2013.

［6］夏伟，胡成，瞿尔仁.ANSYS子模型分析技术在处理应力集中时的应用［J］.工程与建设，2006，20（2）：92-94.

［7］刘令，白雪飞，吴梵.开孔围栏问题有限元分析［J］.船海工程，2011，40（6）：87-91.LIU L，BAI X F，WU F.Finite element analysis of openings with coaming reinforcement［J］.Ship &Ocean Engineering，2011，40（6）：87-91（in Chinese）.