立体几何专题测试卷

■河南省漯河市第五高级中学数学组 刘 惠

编者的话：强化对核心考点的演练、注重对经典题型的归纳,是学好数学的秘诀,基于此,本刊编辑部特开设此栏目,希望同学们能认真对待。从本期开始,如果都能把试卷保存好,对以后的复习大有裨益。

一、选择题

1.已知m,n是两条不同的直线,α,β是两个不同的平面,给出下列命题：①若α⊥β,m∥α,则m⊥β;②若m⊥α,n⊥β,且m⊥n,则α⊥β;③若m⊥β,m∥α,则α⊥β;④若m∥α,n∥β,且m∥n,则α∥β。其中正确命题的序号是( )。

A.①④ B.②④ C.②③ D.①③

2.设l,m,n为三条不同的直线,α,β为两个不同的平面,则下列命题中正确的个数是( )。

①若l⊥n,m⊥n,则l⊥m

②若m⊂α,n⊂α,l⊥m,l⊥n,则l⊥α

③若l∥m,m∥n,l⊥α,则n⊥α

④若l∥m,m⊥α,n⊥β,α∥β,则l∥n

A.1 B.2 C.3 D.4

3.下列说法不正确的是( )。

A.空间中,一组对边平行且相等的四边形一定是平行四边形

B.同一平面的两条垂线一定共面

C.过一条直线有且只有一个平面与已知平面垂直

D.过直线上一点可以作无数条直线与这条直线垂直,且这些直线都在同一个平面内

4.设α,β是两个不同的平面,l是一条直线,则以下命题正确的是( )。

A.若l⊥α,α⊥β,则l⊂β

B.若l∥α,α∥β,则l⊂β

C.若l⊥α,α∥β,则l⊥β

D.若l∥α,α⊥β,则l⊥β

5.已知三棱锥P-ABC的所有顶点都在球O的球面上,△ABC满足AB=22,∠ACB=90°,PA为球O的直径且PA=4,则点P到底面ABC的距离为( )。

A.2 B.22 C.3 D.23

6.如图1,在四面体D-ABC中,若AB=BC,AD=CD,E是AC的中点,则下列命题中正确的是( )。

A.平面ABC⊥平面ABD

图1

B.平面ABD⊥平面BCD

C.平面ABC⊥平面BDE,且平面ACD⊥平面BDE

D.平面ABC⊥平面ACD,且平面ACD⊥平面BDE

7.已知球的半径是1,A,B,C三点都在球面上,A,B两点和A,C两点的球面距离都是,B,C两点的球面距离是,则二面角B-OA-C的大小是( )。

8.如图2,在正方体ABCD-A1B1C1D1中,棱长为1,E,F分别为C1D1与AB的中点,则B1到平面A1FCE的距离为( )。

图2

9.如图3,已知正方体ABCD-A1B1C1D1,E,F,G分别是线段B1B,AB和A1C上的动点,观察直线CE与D1F,CE与D1G。给出下列结论：①对于任意给定的点E,存在点F,使得D1F⊥CE;②对于任意给定的点F,存在点E,使得CE⊥D1F;③对于任意给定的点E,存在点G,使得D1G⊥CE;④对于任意给定的点G,存在点E,使得CE⊥D1G。

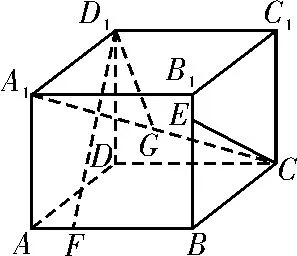
图3

其中正确结论的个数是( )。

A.4 B.3 C.2 D.1

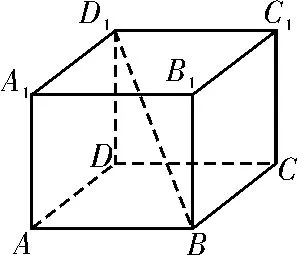
图4

A.3 B.1

C.-1 D.-3

11.如图5所示,在正三棱柱ABCA1B1C1中,AB=2。若二面角C-AB-C1的大小为45°,则点C 到平面C1AB的距离为( )。

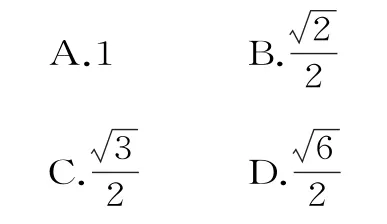
图5

12.下列命题中错误的是( )。

A.如果平面α不垂直于平面β,那么平面α内一定不存在直线垂直于平面β

B.如果平面α⊥平面γ,平面β⊥平面γ,α∩β=l,那么l⊥平面γ

C.不存在四个角都是直角的空间四边形

D.空间图形经过中心投影后,直线还是直线,但平行直线可能变成相交直线

14.如图6,在一个60°的二面角的棱上有两个点A,B,线段AC,BD分别在这个二面角的两个面内,并且都垂直于棱AB,且AB=AC=1,BD=2,则CD的长为( )。

15.在正方体ABCD-A1B1C1D1中,P是正方体的底面A1B1C1D1(包括边界)内的一动点(不与A1重合),Q是底面ABCD内一动点,线段A1C与线段PQ相交且互相平分,则使得四边形A1QCP面积最大的点有( )。

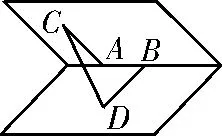
图6

A.1个 B.2个 C.3个 D.无数个

16.过正方体ABCD-A1B1C1D1的顶点A作直线l,使直线l分别与AB,AD,AA1三条棱所成的角都相等,则这样的直线l有( )。

A.1条 B.2条

C.3条 D.4条

金属性接地短路指线路发生接地时，短路电阻数值很小，可以简化为直接接地，如图1.1。最常见的有经弧光电阻接地。金属性短路接地故障点的边界条件为：UA=0；IB=0；IC=0（以A相短路接地为例）。

17.如图7,棱长为2的正四面体ABCD的三个顶点A,B,C分别在空间直角坐标系的坐标轴Ox,Oy,Oz上,则定点D的坐标为( )。

图7

18.二面角的棱上有A,B两点,直线AC,BD分别在这个二面角的两个半平面内,且都垂直于AB。已知AB=4,AC=6,BD=8,CD=217,则该二面角的大小为( )。

A.150° B.45° C.60° D.120°

19.在直三棱柱A1B1C1-ABC中,∠BAC=,AB=AC=AA=1,已知G和E分别为1A1B1和CC1的中点,D与F分别为线段AC和AB上的动点(不包括端点),若CD⊥EF,则线段DF的长度的取值范围为( )。

20.如图8,在棱长为1的正方体 ABCDA1B1C1D1中,E是棱CC1的中点,F是侧面BCC1B1内(包括边)的动点,且A1F∥平面D1AE,沿A1F运动,将B1点所在的几何体削去,则剩余几何体的体积为( )。

图8

21.已知三棱锥S-ABC的每个顶点都在球O的表面上,SA⊥底面ABC,AB=AC=4,BC=215,且二面角S-BC-A的正切值为4,则球O的表面积为( )。

A.240π B.248π C.252π D.272π

22.已知正方体ABCD-A1B1C1D1的棱长为2,其表面上的动点T到底面ABCD的中心O的距离为2,则线段TO的中点的轨迹长度为( )。

A.π B.2π C.3π D.4π

二、填空题

23.长方体的长,宽,高分别为3,2,1,其顶点都在球O的球面上,则球O的表面积为____。

24.已知三棱锥A-BCD中,AB=AC=BD=CD=2,BC=2AD=22,则直线AD与底面BCD所成角的大小为____。

25.A是锐二面角α-l-β的平面α内一点,AB⊥β于点B,AB=3,A到l的距离为2,则二面角α-l-β的平面角大小为____。

26.已知一条直线上有两个点A,B到平面的距离分别为3cm和5cm,则AB的中点到平面的距离为____cm。

27.如图9,在正方体ABCD-A1B1C1D1中,点P在侧面BCC1B1及其边界上运动,并且总是保持AP⊥BD1,则动点P的轨迹是____。

图9

28.P是棱长为2的正四面体内任意一点,则它到该正四面体各个面的距离之和等于____。

29.如图10,在三棱锥A-BCD中,BC=DC=AB=AD=2,BD=2,平面ABD⊥平面BCD,O为BD的中点,P,Q分别为线段AO,BC上的动点(不含端点),且AP=CQ,则三棱锥P-QCO体积的最大值为____。

30.如图11,四面体ABCD的每条棱长都等于2,点E,F分别为棱AB,AD的中点,则

图10

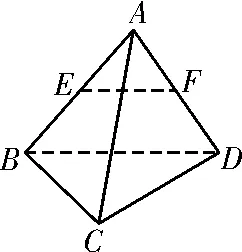
图11

31.如图12,已知边长为1的正△A'BC的顶点A'在平面α内,顶点B,C在平面α外的同一侧,点B',C'分别为B,C在平面α内的投影,设BB'≤CC',直线CB'与平面A'CC'所成的角为φ。若△A'B'C'是以角A'为直角的直角三角形,则tanφ的最小值是____。

图12

32.在三棱柱 ABC-A1B1C1中,侧棱A1A⊥底面ABC,AC=1,AA1=2,∠BAC=90°,若直线AB1与直线A1C的夹角的余弦值是

33.设G是三棱锥V-ABC的底面重心,用空间的一组基向量表示向量____。

34.已知球的表面积为2π,球面上有A,B,C三点。如果AB=AC=2,BC=22,则球心到平面ABC的距离为____。

35.在三棱锥P-ABC中,AB⊥BC,AB=6,BC=23,O为AC的中点,过C作BO的垂线,分别交BO,AB于点R,D,若∠DPR=∠CPR,则三棱锥P-ABC体积的最大值为____。

36.将边长为2,锐角为60°的菱形ABCD沿较短对角线BD折成四面体ABCD,E,F,G分别为AC,BD,BC的中点,则下列命题中正确的是____。(将正确的命题序号全填上)

①EF∥AB;②EF是异面直线AC与BD的公垂线;③CD∥平面EFG;④AC垂直于截面BDE。

37.已知三棱锥O-ABC中,A,B,C三点均在球心为O的球面上,且AB=BC=1,∠ABC=120°,若球O的体积为,则三棱锥O-ABC的体积是____。

三、解答题

38.如图13,四棱锥S-ABCD中,底面ABCD是边长为4的正方形,O是AC与BD的交点,SO⊥平面ABCD,E是侧棱SC的中点,异面直线SA和BC所成角的大小是60°。

(Ⅰ)求证：直线SA∥平面BDE;

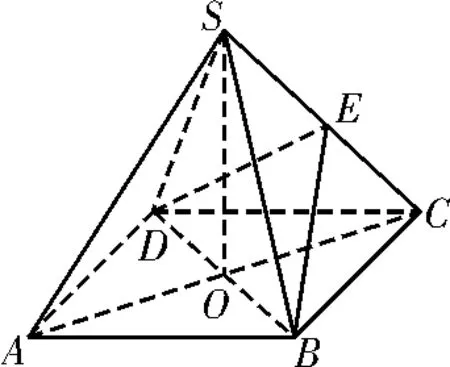
图13

(Ⅱ)求直线BD与平面SBC所成角的正弦值。

39.如图14,已知四棱锥P-ABCD的底面为菱形,∠BCD=120°,AB=PC=2,AP=BP=2。

(Ⅰ)求证：AC⊥PC;

(Ⅱ)求二面角B-PC-D的余弦值。

图14

40.如图15,ABCD是边长为3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE与平面ABCD所成角为60°。

(Ⅰ)求证：AC⊥平面BDE;

(Ⅱ)求二面角F-BE-D的余弦值;

(Ⅲ)设点M是线段BD上一个动点,试确定点M的位置,使得AM∥平面BEF,并证明你的结论。

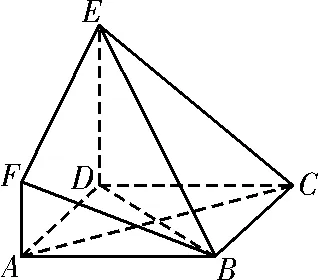
图15

41.如图16,在直三棱柱A1B1C1-ABC中,AB⊥AC,AB=AC=2,AA1=4,D是BC的中点。

(1)求异面直线A1B与C1D所成角的余弦值;

(2)求平面ADC1与平面ABA1所成二面角的正弦值。

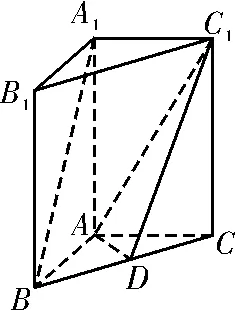
图16

42.如图17,直三棱柱ABC-A1B1C1中,∠ACB=90°,AA1=3,AC=BC=2,D为AB的中点,E为BB1上一点,且

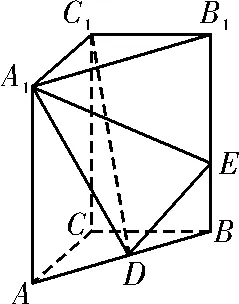
图17

(2)若直线CE与平面A1DE所成的角为30°,求λ的值。

43.如图18,已知正三棱柱ABC-A1B1C1的各棱长都为a,P为线段A1B上的动点。

(Ⅰ)试确定A1P∶PB的值,使得PC⊥AB;

(Ⅱ)若A1P∶PB=2∶3,求二面角P-AC-B的大小。

图18

44.如图19,在直角梯形ABCD中,AD∥BC,AB⊥BC,BD⊥DC,E是BC的中点,将△ABD沿BD折起,使平面ABD⊥平面BCD,连接 AE,AC,DE,得到如图20所示的几何体。

图19

(1)求证;AB⊥平面ADC;

(2)若AD=1,二面角CAB-D的平面角的正切值为6,求二面角B-AD-E的余弦值。

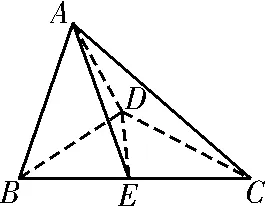
图20

45.如图21,三棱柱ABC-A1B1C1中,已知∠B1A1A=∠C1A1A=60°,AA1=AC=4,AB=2,P,Q分别为棱AA1,AC的中点。

(1)在平面ABC内过点A作AM∥平面PQB1交BC于点M,并写出作图步骤,但不要求证明。

(2)若侧面ACC1A1⊥侧面ABB1A1,求直线A1C1与平面PQB1所成角的正弦值。

图21

46.如图22,在四棱锥PABCD中,PA丄平面ABCD,∠ABC= ∠ADC=90°,∠BAD=120°,AD=AB=1,AC和BD交于O点。

(Ⅰ)求证：平面PBD丄平面PAC。

(Ⅱ)当点A在平面PBD内的射影G恰好是△PBD的重心时,求二面角B-PD-A的余弦值。