透析立体几何中的探索性问题

■山东省肥城市第一高级中学 董欣月

立体几何中的探索性问题立意新颖,形式多样,求解探究过程既能够考查同学们的空间想象力,又可以考查同学们的意志力和探究创新意识,逐步成为近几年高考命题的热点和今后命题的趋势之一。其主要有两类：一是推理型,即探究空间中的平行与垂直关系,可以利用空间线面关系的判定与性质定理进行推理探究;二是计算型,即对几何体中的空间角与距离、几何体的体积等计算型问题的有关探究,此类探究性问题可以转化为关于某个参数的方程,根据方程解的存在性来解决。

透析1——“几何法”探究以“平行”为背景的探索性问题

例1 (2017年吉林百校联盟九月联考)如图1,在四棱锥E-ABCD中,AE⊥DE,CD⊥平面ADE,AB⊥平面ADE,CD=3AB。

(1)求证：平面ACE⊥平面CDE。

图1

(2)在线段DE上是否存在一点F,使AF∥平面BCE?若存在,求的值;若不存在,说明理由。

解析：(1)因为CD⊥平面ADE,AE⊂平面ADE,所以CD⊥AE。又因为AE⊥DE,CD∩DE=D,所以AE⊥平面CDE。因为AE⊂平面ACE,所以平面ACE⊥平面CDE。

透析：求解直线和平面平行的存在探索性问题,一定要灵活利用空间几何体的结构特征,注意其中的平行、垂直及长度之间的关系,取特殊点构造辅助面完成线和面内的直线平行,其中依据性质定理作辅助线和辅助面是关键,本题取ED的三分之一点F构造平行四边形,凸显空间问题平面化的特点。

透析2——“几何法”探究以“垂直”为背景的探索性问题

例2 (2017届广东七校联合体高三上学期联考)在长方体ABCD-A1B1C1D1中,E,F分别是AD,DD1的中点,AB=BC=2,过A1、C1、B三点的平面截去长方体的一个角后,得到如图2所示的几何体ABCD-A1C1D1,且这个几何体的体积为。

图2

(1)求证：EF∥平面A1BC1。

(2)求A1A的长。

(3)在线段BC1上是否存在点P,使直线A1P与C1D垂直?如果存在,求线段A1P的长;如果不存在,请说明理由。

解析：(1)在长方体ABCD-A1B1C1D1中,可知AB∥D1C1,AB=D1C1。由四边形ABC1D1是平行四边形,所以。因为E,F分别是AD,DD1的中点,所以AD1∥FE,则EF∥BC1。又EF⊄面A1BC1,BC1⊂面A1BC1,则EF∥平面A1BC1。

(2)因为VABCD-A1C1D1=VABCD-A1B1C1D1-

(3)在平面CC1D1D中作D1Q⊥C1D交CC1于点Q,过点Q作QP∥CB交BC1于点P,则A1P⊥C1D。因为A1D1⊥平面CC1D1D,而C1D⊂平面CC1D1D,所以C1D⊥A1D1。又QP∥CB,CB∥A1D1,所以QP∥A1D1。

又因为A1D1∩D1Q=D1,所以C1D⊥平面A1PQC1,且A1P⊂平面A1PQC1,所以A1P⊥C1D。由Rt△D1C1Q∽Rt△C1CD,得,所以C1Q=1。又因为PQ∥BC,所以。因为四边形A1PQD1为直角梯形,且高D1Q=5,所以A1P=

透析：求解以特殊几何体为背景的线线垂直关系的探索性问题,常依据几何体的特殊性质,合理选择构造一条直线和另一条直线所在的平面垂直。本题选择C1D和经过点A1且与BC1相交于点P的平面,通过作D1Q⊥C1D交CC1于点Q,过点Q作QP∥CB交BC1于点P,构造出的辅助面为直角梯形。

透析3——“向量法”求解以“角”为背景的探索性问题

例3 (2017年天津市滨海新区八校联考)如图3,在四棱锥PABCD中,PA⊥平面ABCD,AB∥CD,AB⊥AD,PA=AB,AB∶AD∶CD=2∶2∶1。

图3

(1)证明BD⊥PC;

(2)求二面角A-PC-D的余弦值;

(3)设点Q为线段PD上一点,且直线AQ与平面PAC所成角的正弦值为,求的值。

解析：由题意知AB,AD,AP两两垂直,所以以A为坐标原点,以AB,AD,AP的方向为x,y,z轴的正方向建立如图4所示的空间直角坐标系,由题设知B(2,0,0),D(0,2,0),P(0,0,2),C(1,2,0)。

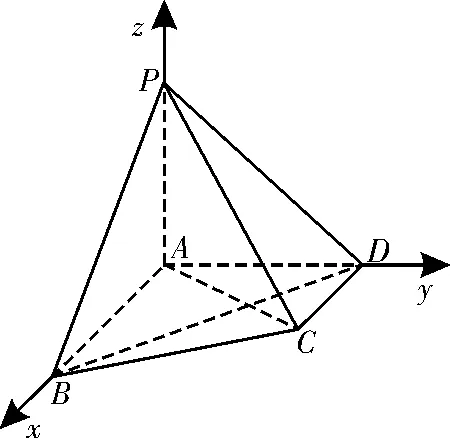
图4

设θ为直线AQ与平面PAC所成的角,而平面PAC的法向量为m=(2,-1,0),

透析：求解与“两异面直线所成的角、直线与平面所成的角和二面角”有关的存在性问题,常利用空间向量法解决,可以避开抽象、复杂的寻找角的过程,只要能够准确理解和熟练应用夹角公式|cosθ|=|cos|可以把“是否存在”问题转化为“点的坐标是否有解,是否有规定范围内的解”等问题。事实说明,空间向量法是探究立体几何中存在性问题的强有力的方法。