全国名校抛物线测试培优卷(B卷)答案与提示

一、选择题

1.B 2.C 3.C 4.A 5.D 6.C 7.C 8.B 9.C 1 0.B 1 1.C 1 2.A 1 3.B 1 4.C 1 5.C 1 6.D 1 7.D 1 8.D 1 9.A 2 0.D 2 1.D 2 2.B 2 3.B 2 4.A 2 5.B 2 6.B 2 7.C 2 8.A 2 9.A 3 0.B

二、填空题

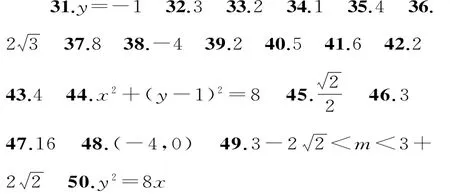
三、解答题

5 1.(1)由抛物线C:y2=2p x(p＞0)过点P(1,-2),可得4=2p,p=2。

从而抛物线的方程为y2=4x,准线方程为x=-1。

(2)抛物线的焦点为F(1,0),所以直线l的方程为y=2x-2。

设点A(x1,y1),B(x2,y2)。

则由韦达定理有:x1+x2=3,x1x2=1。

5 2.(1)抛物线C:x2=2p y(p＞0)的焦点为抛物线C的准线方程为y=由抛物线的定义可知|B F|等于点B到抛物线C的准线的距离。又因为点B到x轴的距离比|B F|小1,所以点B到x轴的距离比点B到抛物线的准线的距离小1,故,解得p=2。所以C的方程为x2=4y。

(2)由(1)得抛物线C的焦点为F(0,1),设直线l的方程为y=k x+1(k≠0),A(x1,y1),B(x2,y2),则

Δ=1 6k2+1 6＞0,由韦达定理得x1+x2=4k,x1x2=-4。

设点O到直线l的距离为d,则S△BOF=

又S△BOF=S△AOD,故|B F|=|A D|。又A,B,D,F在同一直线上,所以

因此,(x2-x1)2=(x1+x2)2-4x1x2=(4k)2-4×(-4),整理得1 6k4+1 6k2-1=

5 3.(1)将E(2,2)代入y2=2p x,得p=1,抛物线方程为y2=2x,焦点坐标为

5 4.(1)因为圆M的圆心在抛物线上且与抛物线的准线相切,且圆半径为3,故b=

因为圆过原点,所以a2+b2=9,a2=

又a2=2p b,故

因为p＞0,所以p=4,抛物线C的方程为x2=8y。

(2)设A(x1,y1),B(x2,y2),P(m,-t),抛物线C的方程为所以y′=

所以x1,x2为方程x2-2m x-4t=0的两根,x1+x2=2m,x1x2=-8t。

5 5.(1)因为点D(1,y0)是抛物线上的点,且|D F|=2,所以解得p=2。故抛物线C的标准方程为y2=4x。

(2)①设A(x1,y1),B(x2,y2)。

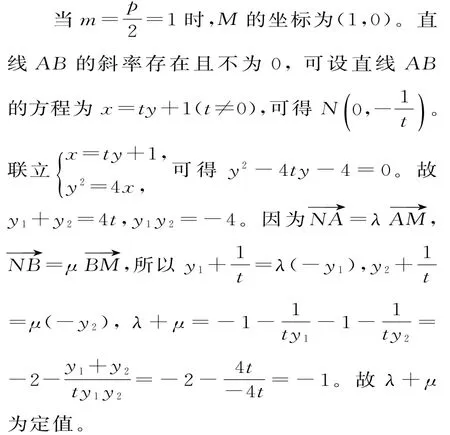
②先取特殊情况探索三条直线A R,B R,MR的斜率之间的关系,当A B⊥x轴时,设A(m,y0),B(m,-y0),R(-m,y3),则

下面证明一般情况成立。

设A(x1,y1),B(x2,y2),R(-m,y3),直线A B的斜率不等于0,可设直线A B的方程为x=t y+m。联立

4t y-4m=0,故y1+y2=4t,y1y2=-4m。

综上可得,三条直线A R,B R,MR的斜率满足kAR+kBR=2·kMR。

(2)设A(x1,y1),B(x2,y2),C(x3,y3),D(x4,y4),则直线A B的方程为y=k1(x-2)。代入抛物线方程得直线A C,B D过点Q(1,0),同理可得y1y3=y2y4=-2,则

5 7.(1)根据题意,点M到点F(1,0)的距离比它到直线x=-3的距离小2,即点M到点F(1,0)的距离与其到直线x=-1的距离相等,则点M的轨迹为抛物线,且其焦点为F(1,0),准线为x=-1,则其轨迹方程为y2=4x。

(2)①联立直线x=m y+1与抛物线的方程,可得y2-4m y-4=0,故y1·y2=-4,x1·x2=1。②设D(-1,y2),则kAO-,所以A、O、D 三点共线。

5 8.(1)抛物线E:y2=2p x(p＞0)的准线方程为,由抛物线的定义可知3-,解得p=2,故抛物线E的方程为y2=4x。

(2)由(1)得抛物线E的方程为y2=4x,焦点为F(1,0)。设直线l的方程为x=m y+1,由消去x,得y2-4m y-4=0。

设A,B两点的坐标分别为A(x1,y1),B(x2,y2)。

5 9.(1)设动点M(x,y),由抛物线定义可知点M的轨迹E是以N(1,0)为焦点,直线l:x=-1为准线的抛物线,所以轨迹E的方程为y2=4x。

(2)点N在以P A为直径的圆C上。

因为n=-m2,所以=0,所以NA⊥NP,点N在以P A为直径的圆C上。