抛物线中的“距离”题解法赏析

■陕西省武功县教育局教研室 李 歆(特级教师)

抛物线是高考数学的必考点,涉及抛物线中“距离”的题目在历年高考中常常出现。同学们处理这类问题时,通常要用到抛物线的定义、两点间的距离公式、直线方程、韦达定理等知识,运算量较大,解题过程复杂。如果根据题目的已知条件和图形的结构特点,灵活运用平面几何知识以及某些特殊的“点”与“线”之间的关系,那么可以简化解题过程,达到高效解题的效果。

1.利用平面几何知识

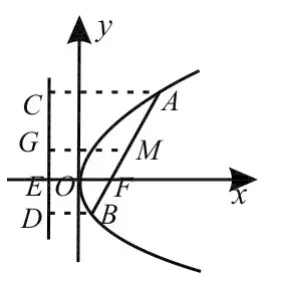
图1

点评:此类题目的一般解法是:先设出直线AB的方程和A、B两点的坐标,然后利用韦达定理求解,这样做比较麻烦,而且在解题的过程中容易出错。相反,利用弦A B以及A、B、F、M点在准线上的射影所构成的特殊图形,采用平面几何中梯形的中位线定理进行处理,却十分简捷,同时还渗透了方程思想。

2.利用焦半径公式

点评:“焦半径公式”是抛物线的一个重要工具。本题如果设直线A B的方程再求解,那么解题中的技巧性要强一些,但以“焦半径公式”开路,很快得到了方程①,从而使两点间的距离公式②的转化方向明确,思路清晰,为最后得到x1搭建了“桥”。

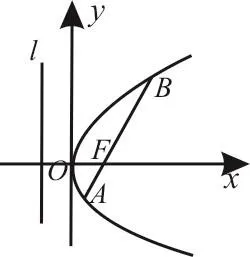
图2

3.利用对称性

A.2 B.4 C.6 D.8

解析：设抛物线C的方程为y2=2p x(p＞0),则焦点为设圆的方程为x2+y2=r2,如图3,则由抛物线、准线、圆均关于x轴对称可知,A、B两点关于x轴对称,D、E两点关于x轴对称,因此,由已知条件可得,因为A、B、D、,整理可得解得p=4,即焦点到准线的距离为p=4,选B。

点评:题中抛物线和圆的方程都不知道,如果根据“已知|A B|=4 2,|D E|=2 5”联想到两点间的距离公式,将两者联立方程求出A、B、D、E的坐标,那么运算过程非常复杂。因此,根据对称性,找出对称点,是顺利求解此题的关键。

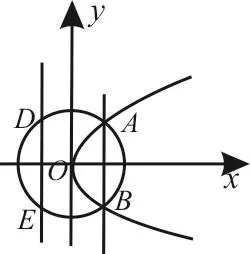
图3

4.利用直线的倾斜角

A.1 6 B.1 4 C.1 2 D.1 0

12斜角为若设A、D两点在x轴上方,B、E两点在x轴下方,如图4,则A点的横坐标为xA=1+|A F|c o sα,B点的横坐标为xB=1-|B F|c o sα,D点的横坐标为xD=1横坐标为xE=1+|E F|c o s|E F|·s i nα。于是由|A F|=xA+1,|B F|=xB+1,|D F|=xD+1,|E F|=xE+1,得|A F|=2+|A F|c o sα,|B F|=2-|B F|c o sα,|D F|=2-|D F|s i nα,|E F|=2+|E F|s i nα,整理得所以,等号当且仅当时成立,所以|A B|+|D E|的最小值为1 6,故选A。

点评:如果采用直线方程或者斜率求解,那么不仅复杂,而且容易出错。根据题设条件及图形结构,引入直线的倾斜角后,则抛物线上的四个点A、B、D、E的横坐标就清晰地显露出来,再结合“焦半径公式”,轻轻松松地就将四条线段|A F|,|B F|,|D F|和|E F|统一用直线的倾斜角α表示了出来,从而使|A B|+|D E|的最小值变得直观了。

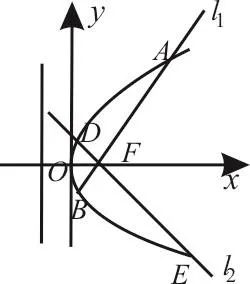
图4

练一练：

1.(2 0 1 7年浙江卷)若抛物线y2=4x上的点M到焦点的距离为1 0,则M到y轴的距离是____。

2.(2 0 1 7年全国Ⅱ卷)已知F是抛物线C:y2=8x的焦点,M是C上一点,FM的延长线交y轴于点N,若M为FN的中点,则|FN|=____。

答案：1.9 2.6

(责任编辑 徐利杰)