铰链四连杆机构的折叠用途设计
王素煦,程武山
(上海工程技术大学,上海 201620)
由于铰链四连杆机构能方便的实现设计的运动轨迹,在工程应用当中的被使用的频率非常高,对其进行运动分析属于经典的分析范畴。折叠功能[1]常常在机构的总体设计中被强调,折叠机构的实现根据其具体的产品与要实现的功能的不同而不同,简单的折叠的机构只需个别铰链或连杆即可,复杂的折叠机构则需要考虑到各个模块的联动、折叠程度与空间安排等方面的影响。
1 设计折叠方案
折叠方案的设计需要根据具体情况而定,不存在处处适用的万能折叠机构,对于简单的铰链四连杆机构来说,其折叠的功能仍可大展身手。以下给出了三种实际案例中应用的折叠方案,均为采用的铰链四连杆机构而设计。方案一为汽车后备箱机构,方案二可应用与简易的飞机起落架机构,方案三为液压传动的铰链四连杆机构,可应用与大型太阳能电池板、卫星盘、射电望远镜的折叠方案。
(1)方案一
如图1所示,为流行的应用于汽车后备箱的铰链四连杆机构[2],其中一个杆子为拉杆,我们可以认为这样的机构具有折叠属性。
(2)方案二
此折叠设计可以应用于简易的飞机起落架机构[3-4],AB外延处为飞机车轮安置处,通过选取合适的杆长与相对位置,通过运动件CD的摆动,可使得AB从动杆绕铰链A做逆时针旋转,带动机轮往右上方折叠,起到起落架的折叠作用,或者说起落功能。
(3)方案三
此方案如图3所示,适用于平面面板的折叠机构,主动杆也为伸缩杆,为液压装置,可应用于大型射电望远镜、太阳能面板、雷达通信设备等设备[5]。图4显示了子方案1中的折叠示意图。
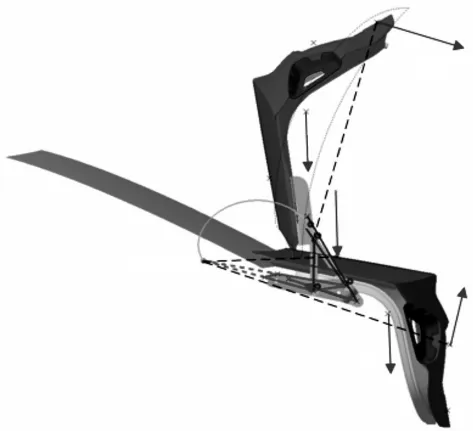
图1 汽车后备箱机构Fig. 1 Automotive trunk mechanism

图2 起落架机构简图Fig. 2 Sketch of landing gear mechanism
2 急回特性分析
图5表示的是铰链四连杆机构的分析急回特性的示意图[6-7],主动件如左下角所示作匀速圆周运动,而从动件作摆动,摆动分为进程和回程,在回程时的速度比进程更快,且其速率的改变剧烈,这种现象就是急回特性。通常情况下将速率慢的进程作为工作行程。如图5所示,AB为主动件,作匀速圆周运动,CD为从动件,作摆动。AB有两个位置使得BC与AB共线,CD标记为C1D和C2D。设t1为AB转动φ1角,而此时C2D摆动至C1D的用时,设v1为C的平均运动速度;同理,AB转φ2角度时,C2D摆动到C1D,用时t2,设v2为C的平均运动速度。设θ为极位夹角,行程速比系数K表征急回特性的程度K:
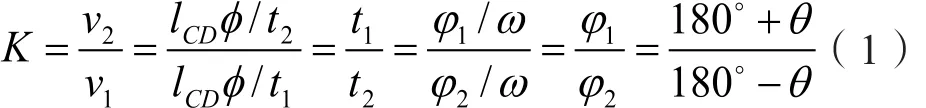
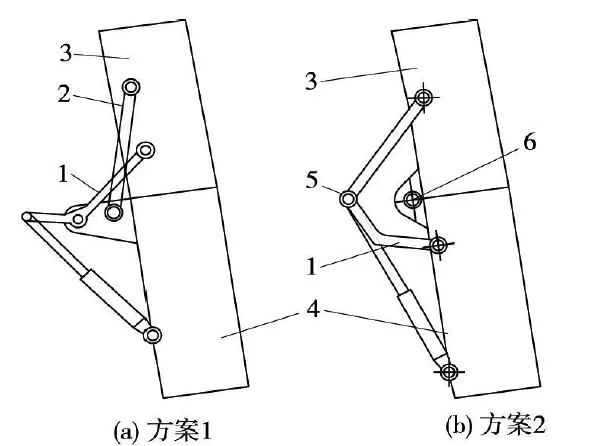
图3 一种面板的折叠机构Fig. 3 Folding mechanism of a panel
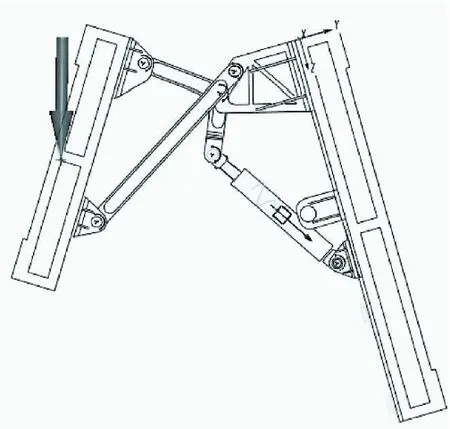
图4 子方案1的折叠示意图Fig.4 Folding sketch of subscheme 1
于是我们知道,θ的大小决定着急回特性的程度。可以设计出不同的杆长与位置,使得θ的大小可以计算与人为控制。
3 运动分析
3.1 瞬心计算
瞬心的计算在机械设计中常常被提及与运用,铰链四连杆的运动瞬心为两个运动连杆l1、l2的交点,如图6所示。
由铰链输入条件可知,以下参数(投影到ZX平面)均为已知,点1(x1,0,z1),点2(x2,0,z2),点 3(x3,0,z3),点 4(x4,0,z4),杆长分别为l1、l2、l3、l4,各个夹角如上图所示,瞬心O坐标(X,0,Z)。
我们可以得出如下的矢量方程:

由上式可得:
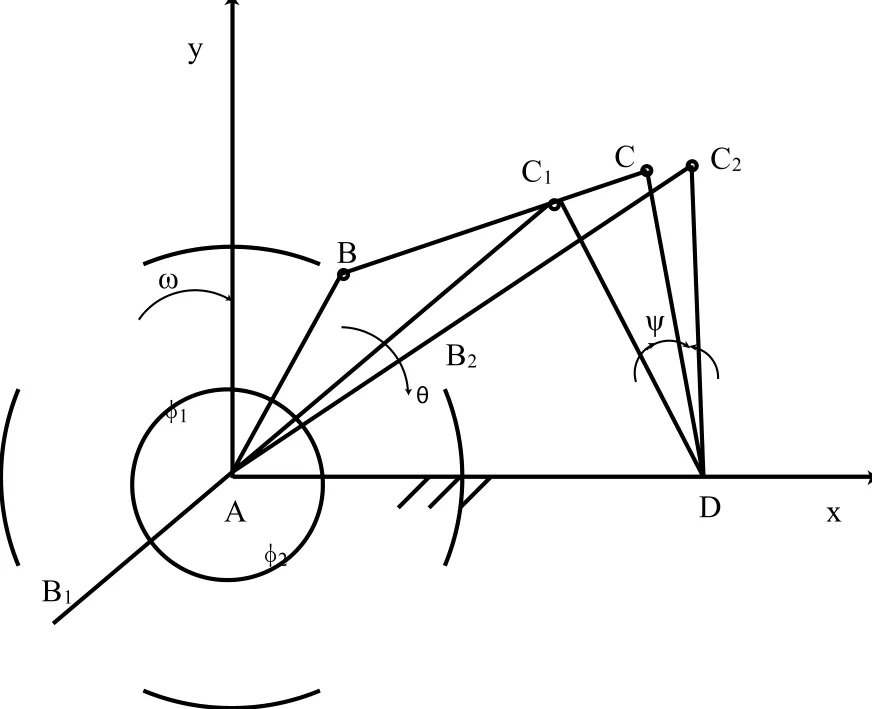
图5 铰链四连杆机构急回特性Fig. 5 Quick return characteristics of hinged four-bar linkages
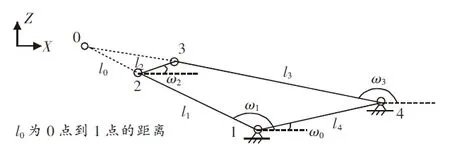
图6 四连杆铰链的瞬心Fig. 6 Instantaneous center of four linkage hinge
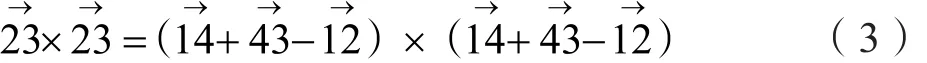
设 A=2l3(l1sinw1-l4sinw0),B=2l3(l1cosw1-l4cosw0),,所以可计算得:
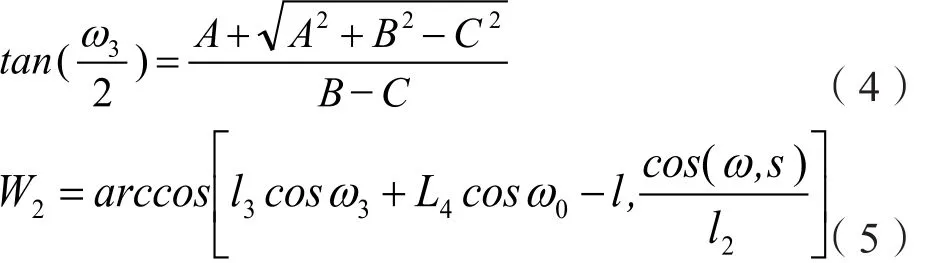
由杆l1和l3所属直线方程可解得瞬心坐标(X,0,Z),其中X=f(z1,z4,x1,x4,ω1,ω3),Z=f1(X,x1,ω1)。
3.2 位置分析
由图7得出:

该方程能够求得方位角θ2、θ3。
将上式分别投影至x轴、y轴上:
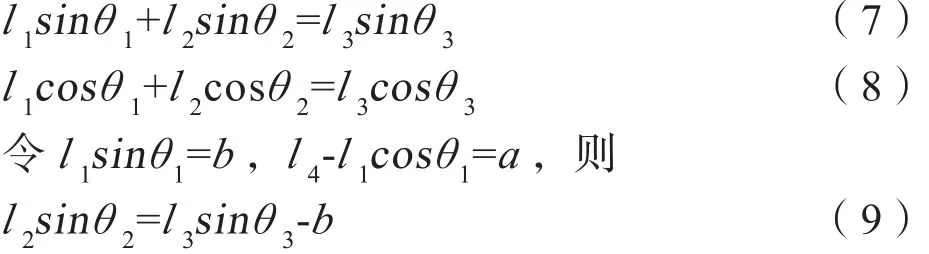
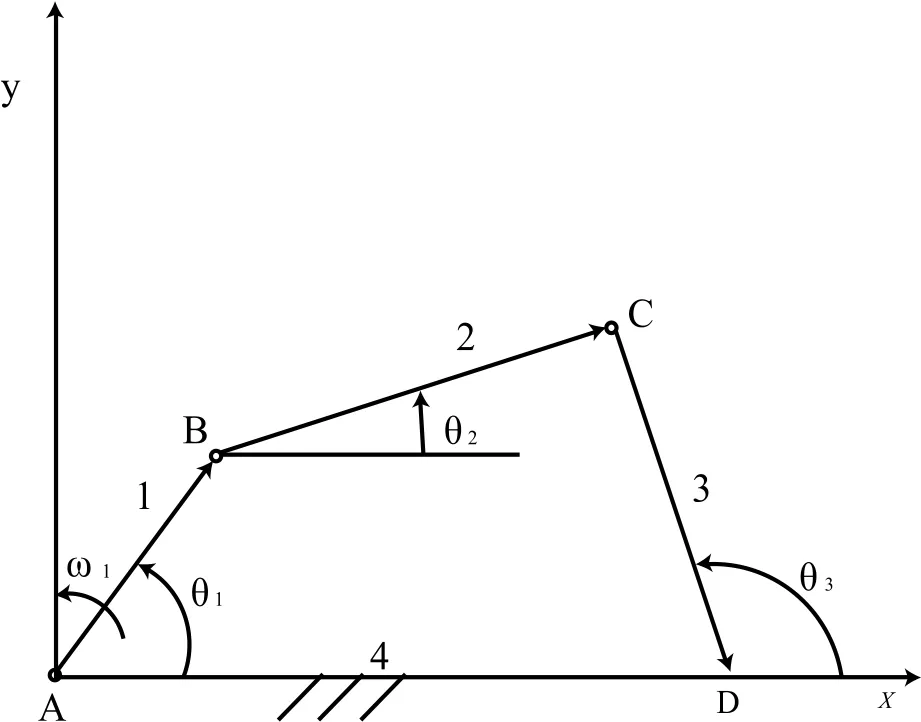
图7 机构矢量表示Fig. 7 Vector representation of mechanism

结合上式可以求出θ2和θ3:
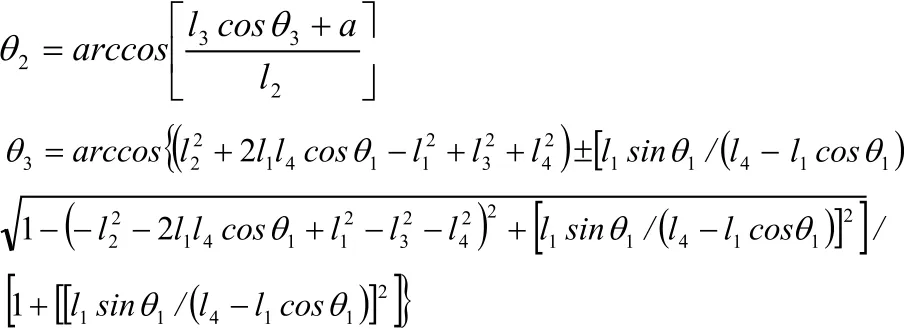
3.3 速度分析
由式(7)、(8)对时间t进行求导而得:
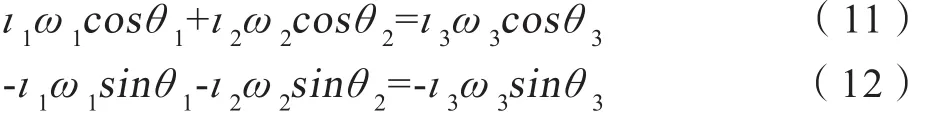
两式联立可得:
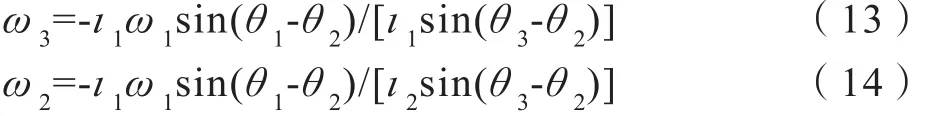
3.4 加速度分析
将式(13)、(14)对时间t求导可以得出:
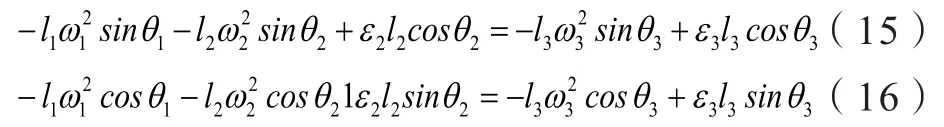
将式(15)、(16)联立求解可得到:
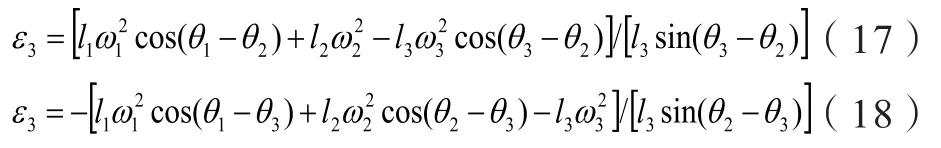
4 仿真分析
4.1 铰链四连杆机构的仿真优化
如图8所示,机架倾角β,AB与AD之间初始夹角φ10,确定决定机构的9个尺寸:xA、yA、a、b、c、d、β、k、γ,输入构件AB的位置角φ1i。
由图8可推出M点的坐标为:
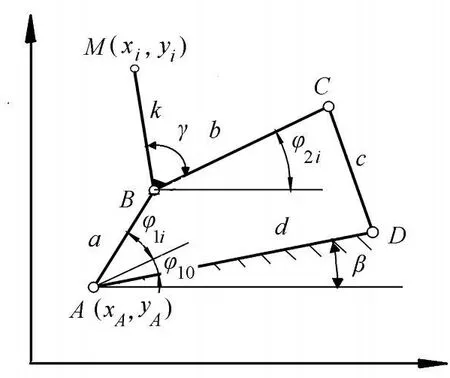
图8 铰链四杆机构示意图Fig. 8 Schematic diagram of four-bar hinge mechanism
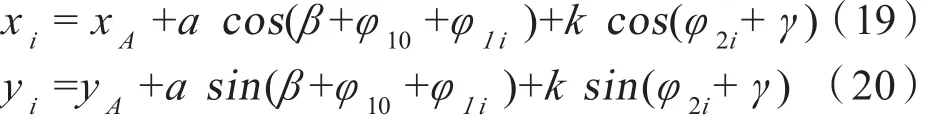
可得在任意的杆长、安装的连杆角与曲柄转动角度前提下的M点坐标。若曲柄转动角是连续的,可以得知M点轨迹为连杆的曲线。
使用Matlab对图8的例子进行仿真,设定初始值为:β=32.6303rad,xA=67mm,yA=10mm。有X0:
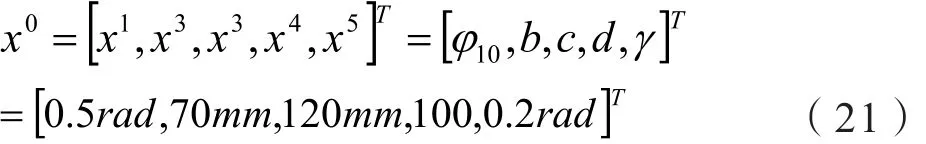
使用Matlab并编辑目标函数以及所需的仿真的M文件,调用的函数如下所示:
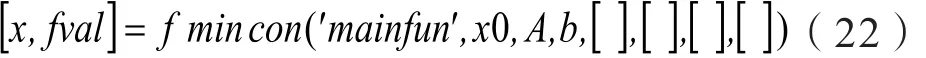
得出以下结果:

如下图9为优化前后的各个点的坐标的对比图,“o”为优化前的轨迹,“+”为优化后的轨迹,可以得知,下图9的点的轨迹能够较好符合,符合对机构的轨迹条件。

图9 优化前后各点的坐标对比图Fig. 9 Comparison of points coordinates before and after optimization.
其轨迹动画仿真如图10。
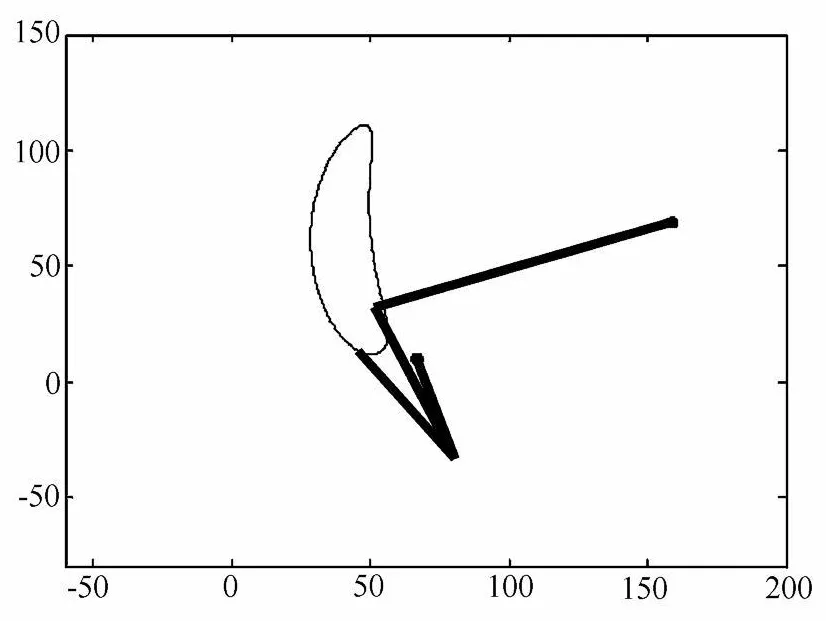
图10 机构的轨迹动画仿真Fig. 10 Trajectory animation simulation of mechanism
4.2 折叠方案三的对比分析
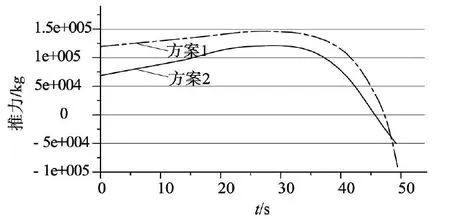
图11 主动件杆反作用力曲线图Fig. 11 Reaction force curve of driving rod
我们对折叠方案三的两种子方案进行仿真分析,在同样的大小空间上求得其最优的铰支点以及驱动件的方位,通过动力学的分析得出两种方案的驱动力大小,进而比较得出最优的传动方案。
我们从图11受力分析中得出,方案1的需要的油缸推动力大致为方案2的双倍。况且从图中得知反作用力的最高点位于折叠机构开始翻转之时,由于反作用力下降,所以力臂也在下降,于是可以吧受力曲线与力臂适当的配合,在符合运动要求下缩减油缸的推动力,得到最优的折叠方案[9-10]。
5 结论
通过以上的设计案例的例举,铰链四连杆机构的运动学分析以及急回特性分析,较为完整的阐述了铰链四连杆机构的研究方法与相关特性,由于本文未涉及到具体系统的折叠需求,无法得出受力情况的分析,但通过对机构的仿真优化与例举案例的仿真,可以得出具有代表性的仿真结果与优化结果。在具体的折叠方案设计中应用的铰链四连杆机构应需要完整的运动学、动力学的分析,得出折叠方案的可靠性。

