基于极限学习机的高铁永磁直驱电机转子位置预测

吕光春，秦斌，祝兴星

（湖南工业大学，湖南 株洲 412007）

0 引言

牵引电机是高速动车组传动系统的核心部件之一，完成从电能到机械能的转换，其性能很大程度上决定了动车组的性能。目前我国的高速动车组的牵引电机主要采用三相异步电机，虽然三相异步电机在大功率应用场合有其独特的优势，然而，其体积和重量大，而效率一般最高能达到94%，而且大多采用强迫通风的方式，使得系统的维护工作量大，噪音也大。三相异步牵引系统的技术特点使得其很难满足新一代牵引系统的性能要求，而永磁同步电机相对于三相异步电机来说，具有更高的能量密度、更高的功率因数和更高的效率等特点；与同容量的异步电机相比，永磁同步电动机可以将体积和重量减少15%～30%。稳定的速度，强大的过载能力，低噪音和高可靠性的优越性能使得永磁同步电机成为新一代牵引电机的不二之选[1-3]。

目前，我国已经开发了用于高速动车组的大功率永磁同步电机，而新一代永磁牵引系统尚处于研究试验阶段。

由于电机驱动系统的强耦合、非线性以及其运行工况的复杂性，使得电机转子位置信息的获取很难通过计算获取，而通常情况下是在电机的转轴上安装物理的位置传感器获取，例如，数字编码器，光电传感器，旋转变压器等。实现矢量控制系统的关键是能够准确地获得转子位置信息。但是安装传感器除增加了系统成本和复杂性之外，还会由于电机内部复杂电磁环境而导致传感器故障从而严重影响到控制系统的性能，降低了控制系统的稳定性。转子位置预测技术可以大大降低了电机驱动系统的成本，减少了维护工作量，提高了系统的可靠性。 目前，针对电机转子位置预测的研究已是日渐成熟，而电机转子位置预测技术大致可分为三种分别是：

（1）依赖于电机自身固有的动态模型的方法，如：直接计算法、模型参考自适应法(Model Reference Adaptive System, MRAS)[4-6]等；

（2）采用现代控制算法对根据电机的非线性模型对其进行线性化来求解并预测出电机转子的位置信息，也称观测器法，如：自适应全阶磁链观测器法[7]、滑模观测器法[8]、人工神经网络、扩展卡尔曼滤波法(Extended Kalman Filters,EKF)[9]等；

（3）利用转子的凸极效应或齿槽效应，采取或注入跟转子运动相关的高频信号，通过这一信号确定转子的位置信息，如转子齿谐波法、高频信号法[10]等。

其中高频信号法是利用定子侧注入的三相平衡高频电压或电流信号来检测凸极位置从而得到转子的转速信息的方法， 这种方法不受电机参数和工作条件的影响，与上述几种方法相比在低速环节有着较高的精度。虽然这种方法不受电机参数和工作条件的影响，但是该法在原理上是利用转子的凸极效应，通过转子的位置变化，引起注入的高频信号的变化，通过高频信号的变化检测转子的位置信息，这就对信号的检测技术需要很高的要求。而且，对于高速动车组这样大容量牵引电机来说，对高频信号频率的选择也有一定的限制。

基于人工神经网络的方法，通常，神经网络和MRAS结合构成MRAS- Neural Net控制，以经过训练的神经网络作为模型参考自适应系统的可调模型。使用误差反向传播算法代替自适应法则来估计转子的位置。核心思想是使用神经网络无限接近任何非线性系统的能力，以表现其出色的识别精度。目前，该方法常与其他现代先进算法组成神经网络自适应的预测模型，从而成为研究的一个热点[11]。对于神经网络一般采用多层隐含层神经元结构，采用梯度下降法对网络进行求解，这样一来，虽然提高了网络的精确度，但是网络结构的建立依赖于网络中的多个参数，也增加了训练的时间，这种需较长时间进行计算的算法用于检测和预测电机转子的位置效果较差。本文将采用单隐层反馈神经网络(Single-hidden Layer Feedforward Neural Networks)，使用ELM算法进行网络的求解。

ELM是南洋理工大学黄广斌（Guang-Bin Huang）教授于2006年提出的一种新算法，用于求解SLFNs。与之前的传统采用梯度下降的训练方法相比ELM实际上是将对网络非线性方程组的求解简化为对线性方程簇参数的求解，因此ELM方法具有收敛速度快，避免了梯度下降容易造成的局部解，提高了求解网络的泛化性能等优点[12]。ELM通过学习同样能将复杂而又庞大的非线性映射准确表达出来。本文将介绍高速动车组用永磁同步电机的矢量控制系统及其特点，重点分析引入ELM算法对电机的转子信息进行检测，并进行仿真验证。

1 牵引用永磁同步电机数学模型

作为高速动车组的牵引电机，需要在十分恶劣的工况下长时间运行，对电机的性能要求十分苛刻。随着对牵引性能的要求不断提升，及绿色发展的需要，永磁同步电机越来越凸显它的优越性。根据牵引系统运行的性能要求，经过合理的设计，牵引用永磁同步电机选用了永磁体内置式结构，内置式永磁同步电机(Interior Permanent Magnet Synchronous Motor, IPMSM)结构机械性能更好，磁阻转矩能得到更好的利用，有更好的系统兼容性，同时电机的恒功区更宽[13]。因此本文将采用用于高速动车组的内置式永磁牵引电机进行数学建模和转子位置检测和预测。

在一系列假设条件下[14]，在d-q轴系下列写的IPMSM的磁链方程、电压方程、转矩方程如下：

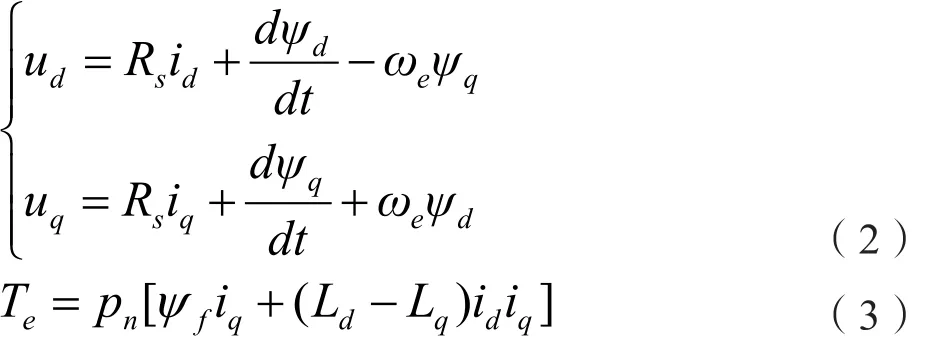
上式中ψd、ψq为d-q坐标系下的定子磁链分量，ψf为内置于转子永磁体磁链，Rs为定子电阻，Ld、Lq为直、交轴同步电感分量，ωe为定子磁链矢量的角频率，id、iq为定子电流矢量在直轴和交轴上的电流分量，ud、uq为定子电压矢量在直轴和交轴上的电压分量，Te为电机的电磁转矩。

对于同步电机，有：

式中ωr为转子的位置。

将（1）、（4）式带入（2）式得：

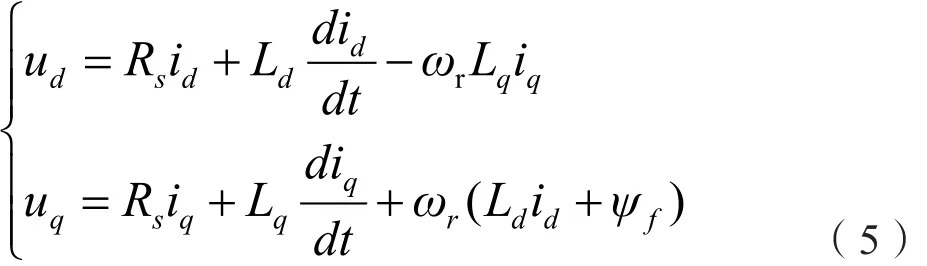
从（5）式可以看出，在d-q轴系中以及电机参数确定的条件下，转子的位置只与d-q轴系下的电压、电流及电流变化量有关。而d-q轴系下的电压、电流是由自然轴系通过线性变换得到，即可将上述方程描述为转子的位置与定子电压矢量和定子电流矢量相关。同时，由于永磁直驱电机的运行是一个动态过程，其状态的变化前后密切相关。

2 基于极限学习机的IPMSM位置参数预测原理

IPMSM基于id=0的矢量控制框图如图1所示，其控制性能主要依赖于对电机转子位置信息的准确提取，传统方法是位置传感器安装在转轴上，然后用经过训练的极端学习机代替位置传感器，以检测电动机转子的位置，但是这种方法因电机固有的机电和检测电路的延迟使得到转子的位置信息的检测具有一定的滞后性。

对于SLFNs结构如图2所示，ELM通过生成随机的初始化输入权重和输出层的偏置，导入输入、输出训练数据就可确定并得到相应的输出权重，进而确定整个的网络结构。

由图2可知，可以将一个样本为N，具有L个隐含层神经元的SLFNs表示为：

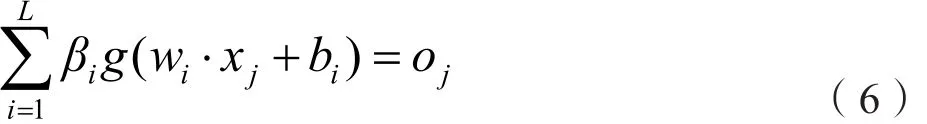
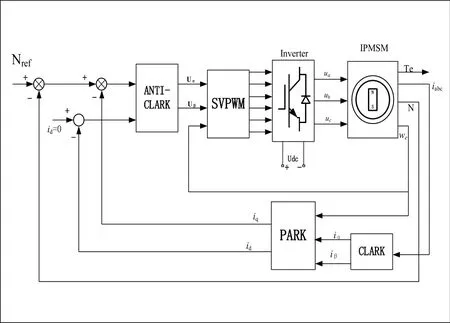
图1 IPMSM基于id=0的矢量控制框图Fig.1 Based on rotor field oriented control block diagram

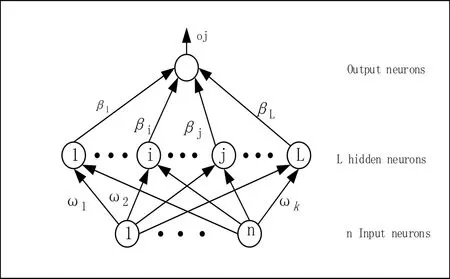
图2 单隐层神经网络结构图Fig.2 SLFNs structure chat

其中j=1,2,…,N，wi为输入权重，βi为输出权重，bi是第i个隐含层单元的偏置，oj为网络的输出。wi·xj表示wi和xj的内积。

在上文建立的IPMSM动态数学模型中，可以发现在d-q轴系下的电机电压方程中虽含有电机的转子位置信息，但是电机的强耦合性、非线性，使得转子的信息很难准确地通过计算提取，但是通过试验取得的实际数据训练的SLFNs可以逼近任意的非线性方程。根据这一特点，通过获取易取得的定子电压、电流，与储存在寄存器中前一时刻获取的电机转子的位置和转速，使用SLFNs逼近当前定子电压和电流、前一时刻位置和转速与当前电机位置和转速、下一时刻转子位置、电磁转矩的关系。

对于一个用于逼近这种复杂关系的SLFNs，其输入层、输出层分别为：

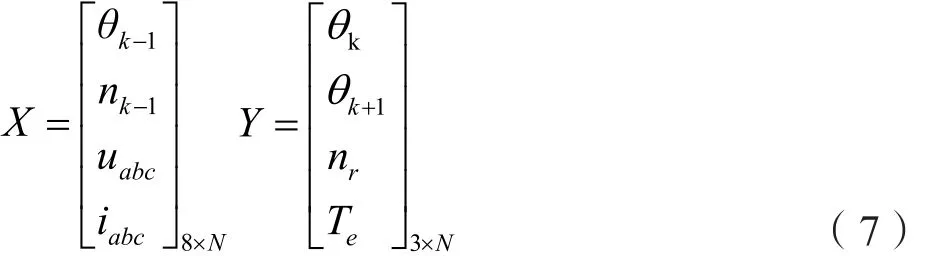
其中，N为训练数据数量，X为输入变量矩阵，Y为输出变量矩阵。θk-1为上一时刻转子位置，nk-1为上一时刻转子的速度，uabc=[uab,ubc,uca]T为定子三相电压，iabc=[ia,ib,ic]T为三相定子电流，θk为当前时刻转子的位置，θk+1为下一时刻转子位置的输出，nr为当前时刻转子的速度，Te为当前时刻电机的电磁转矩。

由上述确定了输入层有8个神经元，对应着8个输入变量，假设隐含层有L个神经元，对应L个隐层节点，输出层有4个神经元，对应4个输出变量，设隐含层神经元的激活函数为g(x)，则期望的该单隐层神经网络的输出T为可表示为：

采用ELM算法的单隐层反馈神经网络学习目标是使得确定上文所提到的网络的输出权重，确定网络结构并最小化网络输出和实际输出之间的误差，即：

即存在βi，wi和bi使得

得到：

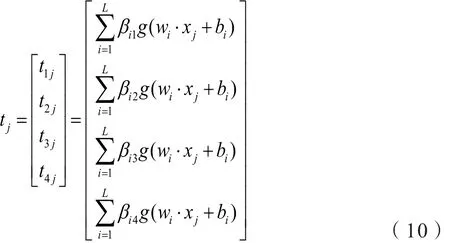
其中，j=1,…,N，wik表示输入权重，βik表示输出权重。

式（8）可表示为：

其中矩阵T’为矩阵T的转置；矩阵H为神经网络的隐含层输出矩阵，具体形式如下：

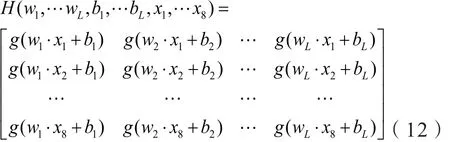
对于矩阵H的求解，解决这个问题的传统方法是采用梯度下降法，但是该算法需要在迭代的过程中调整所有参数。而在ELM算法中，随机确定输入权重wi和隐层的偏置bi后，通过确定一个无限可微的激活函数，隐层的输出矩阵就被唯一确定。就这样对单隐层神经网络的求解就等同于求解线性系统Hβ=T，并且输出权重β可以被唯一确定。

其中，H+是矩阵H的Moore-Penrose广义逆。且可证明求得的解的范数是最小的并且唯一。

3 ELM算法的实现和仿真

3.1 ELM算法的实现

根据上述分析，ELM学习算法主要是以下几个步骤：

（1）训练数据的处理和导入。

（2）根据不同隐含层神经元数量对训练精度和测试精度的影响，确定更好的隐含层神经元的数量L，并且随机确定输入层的权重wi和隐含层神经元的偏置bi。

（3）反复使用不同的无限可微的函数确定一个较好的隐含层神经元的激活函数g(x)。

计算隐含层输出矩阵H。

计算输出层权重βi。

3.2 仿真验证

本试验选取用于高速动车组牵引系统的IPMSM。电机参数如下：极对数Pn=6，定子电阻Rs=0.262 Ω，直轴电感Ld=0.00521 H,交轴电感Lq=0.00951 H，永磁体磁链ψf=1.6 Wb,转子的转动惯量J=0.85 kg*m2，阻尼系数F=0.0013 N*m*s,变流器中间直流电压Udc=3500 V，额定转矩TL=1364 N*m，设定转速1200 r/min，假设电机负载转矩为外界的扰动。先搭建高速动车组永磁直驱电机矢量控制模型，调整参数之后取得ELM的训练数据，再经如图3所示的数据处理及训练过程，得到ELM的学习模型。

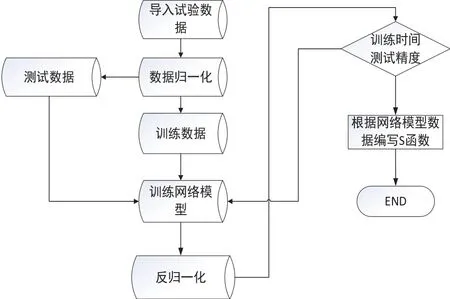
图3 数据处理及训练流程图Fig.3 Data processing & training flow diagram

本试验采用10000个数据组成的ELM的训练数据集和2500个数据组成的测试数据集，并以sigmoid函数为激活函数，训练过程及结果如下：

（1）进行多次训练，根据隐含层神经元的数目与训练精度和测试精度的关系，然后可以确定一个优质的隐含层神经元的数量。仿真结果如图4所示。

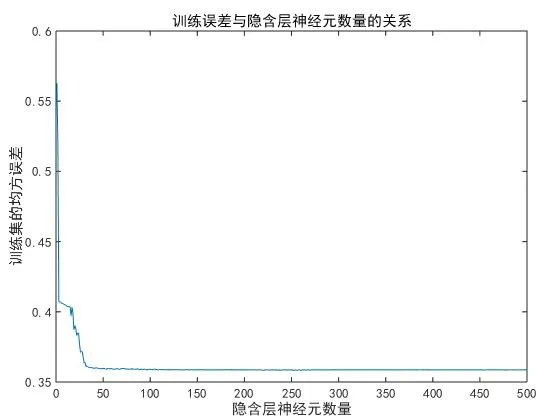
图4 训练误差与隐含层神经元数量的关系Fig.4 The relationship between training error & the number of hidden neurons

图5 测试误差与隐含层神经元数量的关系Fig.5 The relationship between testing error & the number of hidden neurons

（2）根据第一步的仿真结果，选取250个隐含层神经元，采用2500个测试数据，求得SLFNs与测试数据中输出值的绝对误差，及网络预测输出的转子位置的当前值和测试集输出间的跟随关系。以下图中E表示ELM与测试数据输出值的平均误差，R表示SLFNs的输入数据与输出数据的相关性，根据网络的输入数据确定当前时刻转子位置的仿真结果如下：

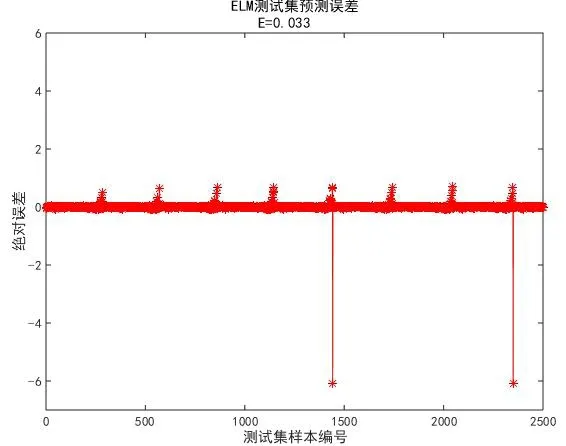
图6 2500个样本的测试集的绝对误差Fig.6 Absolute error of the testing gather for 2500 samples

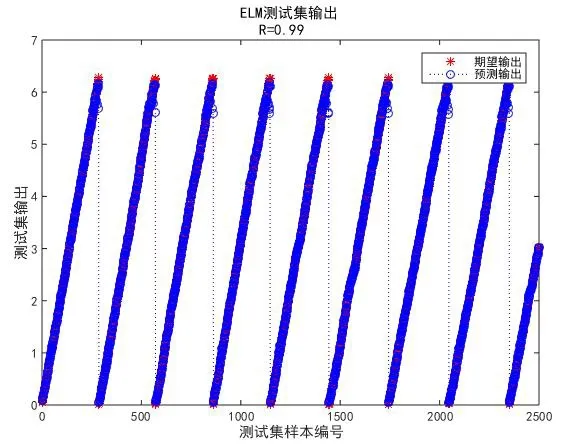
图7 2500个样本的测试集的期望输出与预测输出Fig.7 Expected & predicted output of the testing gather for 2500 samples

（3）又选取250组测试数据进行测试，根据网络的输入所确定的当前时刻转子位置的仿真结果如图8、9所示。

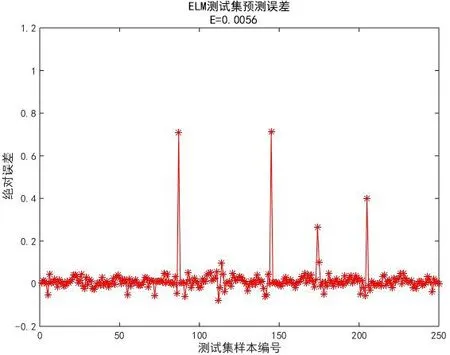
图8 250个样本的当前时刻转子位置测试集的绝对误差Fig.8 Absolute error of the testing gather for 250 samples in the sample time

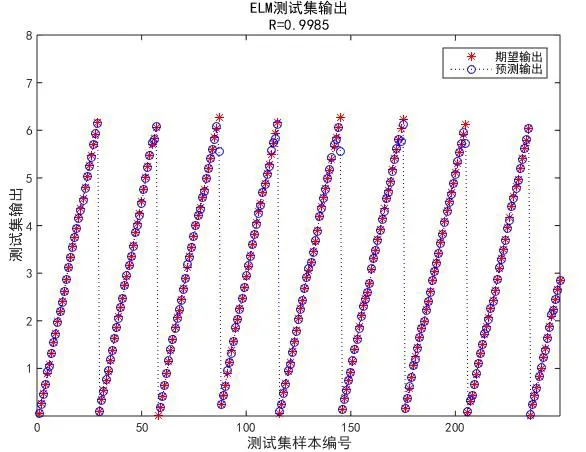
图9 250个样本的当前时刻转子位置测试集的期望输出与预测输出Fig.9 Expected & predicted output of the testing gather for 250 samples

（4）选取250个样本测试的根据ELM的输出所确定下一时刻网络输出与实际输出的关系，如图10、11所示。

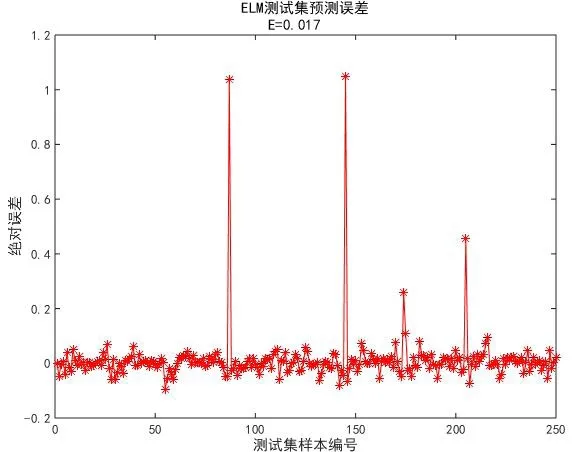
图10 250个样本的下一时刻时刻转子位置测试集的绝对误差Fig.10 Absolute error of the testing gather for 250 samples in next sample time

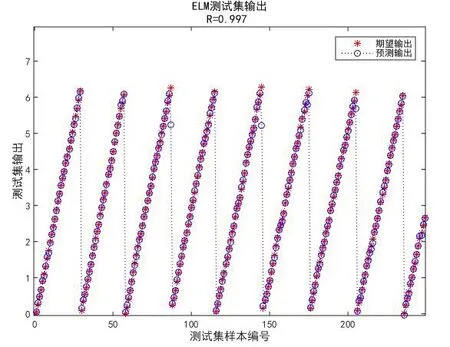
图11 250个样本的下一时刻时刻转子位置测试集的期望输出与预测输出Fig.11 Expected & predicted output of the testing gather for 250 samples in next sample time

4 结果分析以及展望

以上试验结果说明，将ELM引入永磁直驱电机的转子位置估计与预测系统中，在给定训练数据和测试数据后，经过学习，ELM能够对永磁牵引电机的转子进行检测和进一步的预测并且能够跟随转子位置的变化而达到足够的精度，预测值也相当精确，它还具有相当快的学习能力，动态性能良好，响应速度足以实现对转子位置进行检测和预测的要求，也可以使用ELM取代物理的位置传感器。本试验中将电机的电磁转矩也作为网络的输出，试验结果表明，ELM同样具有对电机转矩观测的能力。但是，由于ELM算法下的SLFNs的输入权重wi和隐含层神经元的偏置bi是随机确定的，确定的网络参数可能达不到最优的参数，并且在反复试验时，这种随机确定的参数造成了神经网络参数不一致，导致试验结果略有差异，但是在选择相同输入参数前提下，相同的隐含层神经元数目时误差不大。总体来看，试验结果达到预期效果。

根据高速动车组永磁牵引系统的工作特征，下一步将对永磁直驱电机采取直接转矩空间矢量(DTC-SVPWM)控制，利用ELM实现对永磁牵引电机的转子位置、磁链和转矩同时进行观测和预测，实现永磁牵引电机的期望电压矢量直接转矩预测控制，进一步降低牵引电机的转矩脉动，以追求更好的控制性能。