拓宽视角 提升能力

顾寒平

摘 要：现行苏教版教材的例习题具有较强的基础性、典型性、示范性和迁移性，反映了相关数学理论的本质属性，蕴含着重要的数学思维方法。教师应该对这些例习题教学改编、挖掘和拓展，使教材例习题在初三的复习中进一步发挥作用，提升学生的能力。本文以“矩形折叠的再探究”复习课为例，对如何提高初三专题复习的有效性谈谈个人的一些尝试。

关键词：拓展视角;专题复习;教学实践

中图分类号：G633.6文献标识码：A     文章编号：1992-7711（2018）23-063-2

“矩形折叠”在苏教版八年级数学教材第九章《中心对称图形——平行四边形》的复习题中已探究过，但随着学生数学知识和数学经验的积累，数学能力的不断提升，有必要引导学生从不同的视角进行深度探究，拓宽学生数学的视角，进一步提升学生的数学能力。

一、教学设计与简析

问题1：如图，在矩形ABCD中，AB=6，BC=10，点P为AB边上一动点，将矩形沿CP折叠，使顶点B与点E重合。

（1）如果点E落在AD边上时（如图①），求线段PB的长。

（2）如果点P与点A重合（如图②），求DN的长。

（3）如果点E落在AD边的上方，且ME=MA（如图③），你能求线段PB的长吗？

（4）点P从点A移到点B的过程中，点E运动的轨迹有规律吗？

简析：前两问主要引导学生回顾矩形、轴对称、全等、相似、等腰三角形、直角三角形等相关的概念和性质，以及处理基本图形的方法和数学思想。图①②是矩形折叠的两个基本图形。基本图形①是使矩形的一个顶点落在矩形的一边上。这里利用的主要知识有：矩形、轴对称的性质、勾股定理、△APE∽△DEC;基本图形②是使矩形沿着对角线折叠。这里利用的主要知识有：矩形、轴对称的性质、△AEN≌△CDN、折叠后重合部分△ACN是等腰三角形;第（3）问既是前两问的变式巩固，也为下一问的难点作好铺垫。难度有所提升，但有了前面两问的铺垫应该不難解决。这里利用的主要知识有：矩形、轴对称的性质、勾股定理、△AMP≌△MNC∽△DCN;第（4）问拓展我们对矩形折叠的视角，最大的难点在于如何想到点E的轨迹是以点C为圆心，CE长为半径的圆弧。这既要从“动”中找出“静”的量，又要对“圆是到定点距离等于定长的点的集合”基本概念的理解。因此尝试让学生先画出大概图像，再从数学的角度去理解。铺垫的三种情形是突破口。

问题2：如图，在矩形ABCD中，AB=6，BC=8，点P为AD边上一动点，将矩形沿CP折叠，使顶点D与点F重合。

（1）如果点F落在对角线AC上时，求线段PD的长。

（2）如果点B、F、P三点在同一直线上时，求线段PD的长。

（3）如果点F落在矩形对称轴上时，求线段PD的长。

简析：由问题1中的拓展经验可知，点F随着折痕CP位置的变化而变化，点C是定点，CF恒等于定长CD，所以点F的运动轨迹是以点C为圆心，CD长为半径的圆弧。先把点F定下来：（1）点F落在对角线AC上时，点F是⊙C与AC的交点如图⑤;（2）点B、F、P三点在同一直线上时，BP是的⊙C的切线，切点为F如图⑥;（3）当点F落在矩形对称轴上时，点F是⊙C与矩形对称轴的交点。再根据轴对称的性质作出相应的图形分别如图⑦—⑩。

主要方法：第（1）问中的图⑤是三角形折叠的基本图形，可以利用△APE∽△ACD或勾股定理（Rt△APF）求解;第（2）问图⑥可以利用△ABP≌△FCB或△BCP是等腰三角形轻松求解;较困难的是第（3）问的求解，矩形的对称轴有横竖两条直线，点F的轨迹与对称轴可以交在矩形内，也可点交在矩形外。图⑦由CF=CD=2CJ，得到∠FCJ=60°，利用含特珠角的Rt△CDP求解;图⑧这种情形显然不存在;图⑨利用△PGF∽△FHC求解，这种解法在问题1中已回顾过;图⑩还是利用△PGF∽△FHC求解，通过计算得到点P在射线DA上，说明不存在。

上述两环节教学时，教师应给予学生充足的思考时间、充分的表达空间和有效的实践机会，让学生进行独立思考、动手画图、猜想验证等学习活动，对问题进行思辨、优化，以提升学生的数学学习能力。

二、链接思考

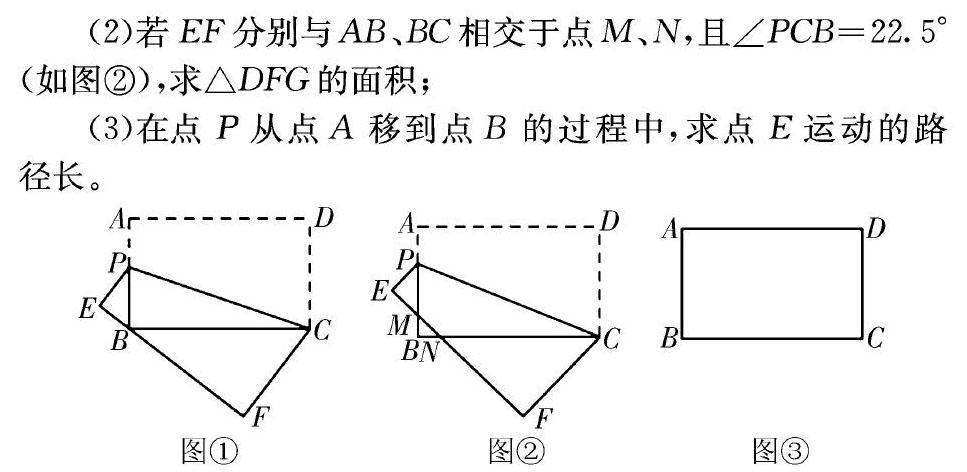
如图，在矩形ABCD中，AB=1，BC=3，点P为AB边上一动点，将矩形沿CP折叠，使顶点A、D分别与点E、F重合。

（1）当EF恰好经过点B时（如图①），求线段AP的长;

（2）若EF分别与AB、BC相交于点M、N，且∠PCB=225°（如图②），求△DFG的面积;

（3）在点P从点A移到点B的过程中，求点E运动的路径长。

三、课堂生成

生成片断1：问题1中第（4）问

师：点E和点P是关于折痕CP对称，点E随着点P的运动不停的变化，点P从点A移到点B的过程中，点E运动的轨迹有规律吗？

（动手画图、猜想验证……）

生：应该是圆弧吧。

师：你是怎么猜出来的？

生：我找了几个特殊点，大概画了一下。

师：你找了哪几个特殊点呢？

生：就上述三种情况的三个点，再找了一个点B。

师：既然是圆弧，那圆心是谁，半径是多少呢？

生：点E随着折痕CP位置的变化而变化，点C是定点，CE恒等于定长CB，所以点E运动的轨迹是以点C为圆心，CB长为半径的圆弧。

等大部分同学画出路径后，教师拖动点P在AB上运动，追踪点E的轨迹。通过几何画板的演示，让学生更加直观的认识点E的轨迹。

师：其实，在解决一些动点问题时，我们可以将问题特珠化，通过特珠情形来帮助我们理解动点的问题。解题时我们还要关注前面的问题设置，它有时就是我们解题的“梯子”。

生成片断2：问题2中第（3）问

师：当点F落在矩形对称轴上，你能找到这个点吗？

生：矩形的对称轴有两条，我们要分类讨论。

师：很好，为了看得清楚，我们将两条对称轴分开画。

生：找到了，分别如图⑦⑨这两种情形。

师：你是怎么找到的？

生1：先画对称轴，再画点F的轨迹⊙C，然后根据轴对称的性质找到点P。

师：有不同的看法吗？

生2：还有如图⑧⑩两种情形呢？

学生开始争论起来……最后达成共识：圖⑧这种情形直观判断显然不存在;图⑩这种情形要通过计算判断是否可以。

师：经过讨论，我们达成了共识要求解图⑦⑨⑩两种情形。先求谁比较简单呢？

（学生独立思考……）

生1：先求图⑨，它就是问题1中图①的情形;再求图⑩，它是图⑨的变形，“形变神不变”还是可以利用△PGF∽△FHC解决;最后求图⑦，过点P作一条直线与AB平行就构造了图⑨的情形。

生2：先求图⑦，它比较特殊：CF=CD=2CJ，得到∠FCJ=60°，利用含特珠角的Rt△CDP求解。

（生师共同交流，对问题进行思辨、优化……）

四、启示与反思

1.教学设计要回归课本

课本中的一些经典例习题，潜力大、功效多，内涵丰富、韵味无穷。作为教师，我们应精心钻研教材，科学合理安排，深入挖掘利用，发挥教材中例习题的潜在功能，努力创设问题的情境，引导学生去思考、探索，使学生在消化吸收课本经典例习题的基础上有所发现、有所创新。就能极大地提高学生的学习主动性和积极性，就能充分发挥教材的创造性作用。

2.教学设计要深入浅出

前苏联心理学家维果斯基的“最近发展区理论”，认为学生的发展有两种水平：一种是学生的现有水平，指独立活动时所能达到的解决问题的水平;另一种是学生可能的发展水平，也就是通过教学所获得的潜力。两者之间的差异就是最近发展区。教师应着眼于学生的最近发展区，为学生提供带有难度的内容，调动学生的积极性，发挥其潜能，超越其最近发展区而达到下一发展阶段的水平，然后在此基础上进行下一个发展区的发展。

鉴于此，在设计初三复习课时，教师对学情一定要正确把握，对教学内容的选择一定要深入研究。复习课不是知识点的回忆及简单问题的罗列与堆砌，问题设计要有一定的思维量，要让学生的思维处于高水平的认知活动中。

3.教学中重视数学思想方法的渗透

初中数学内容的整体结构有两个有力的支柱，即数学知识与数学思想方法。数学知识蕴藏着思想方法，数学思想方法又产生数学知识，二者缺一不可。

本节课探究活动过程中始终引导学生抓住轨迹是圆弧这条主线，注重数学问题解决过程中的数学思想方法的渗透，把原来的结论内化成了现在的解题方法，使学生的能力得到了进一步的提升。

4.教学中重视基本图形的提炼

读图、识图、画图、分析图形是初中学生学习几何知识的基础，很多几何知识是通过图形来传递、表达的，我们通常把这些图形称之为基本图形。图形可以引发联想，形成新的图形，使知识得以有效拓展，以优化和发展学生的数学认知结构，发挥其创造力。