我国保险股市场风险度量的比较研究——来自VaR-GARCH族模型的证据

李 佳，陈冬兰

（上海理工大学 管理学院，上海 200093）

一、引言

保险作为金融体系与社会保障体系的重大支柱，与我国经济社会的发展紧密联系在一起，具有分散风险和经济补偿两个基本功能，此外，包括给付保险金、融通资金、储蓄、防灾减灾、社会管理等功能[1]。近年来，伴随着保险业日新月异的变化和不断的深化发展，保险行业逐渐变成了资本市场的宠儿，投资者除了购买保险公司的理财产品外，还将通过购买保险公司的股票来进行投资,随着股票投资的日渐增加，如何衡量其面临的风险显得尤为重要。目前，我国A股上市保险公司有中国人寿、中国平安、中国太保、新华保险。其中，中国人寿、中国平安、中国太保于2007年A股上市，新华保险于2011年以A+H股方式同步上市。2017年，根据相关财务指标显示，主营收入和净利润排名前三的分别为中国平安、中国人寿、中国太保。实证研究方面，20世纪90年代，H.Markowitz研究各种风险度量方法，最终确定方差作为测试风险工具，往后，William Sharp提出CAPM模型，使用单只证券标准差度量其风险，归于方差法中[2]。以方差方法衡量风险，存在一定缺陷。如投资者对高估与低估投资结果均给以相同的权重，不符合实际情况。对此，大量学者提出了改进，刘庆富（2006）通过VaR方法对我国铜期货市场进行了风险度量[3]。邹正方（2010）用VaR方法研究商业银行外汇风险，结果表明，VaR方法计算外汇资产的风险补偿金，可以有效预测和控制外汇风险[4]。Jhe-Jheng（2018）用 Copula-GARCH 模型计算出VaR值，用以估计信用违约互换投资组合风险，测量风险的绝对值，主要以投资者资产的最大损失为依据[5]。VaR方法近年来很盛行，比方差法度量风险更简洁，更直观。本文选取规模最大的中国人寿、中国平安、中国太保三家保险公司的收盘价作为研究对象，在VaR风险价值方法的基础上，建立GARCH类模型，对三家上市险企股票波动价值风险以及各类模型进行比较分析，得出对投资者有参考性的结论。

二、VaR-GARCH族方法的理论概述

VaR方法（Value-at-Risk）是目前众多金融机构的风险控制管理的主流方法。VaR（在险价值）即在市场波动正常的情况下，在未来特定时期内金融资产（或组合）价值的Max可能损失[6]。表达式：

其中VaR为正值，ΔPΔt为某一资产在Δt持有期的价值损失额，p为资产价值损失小于等于给定置信水平α下的在险价值（Max可能损失）。置信水平 α：通常为 99%（BCBS，1997） 或 95%（JP Morgan），置信度越大，VaR越大。

计算VaR值普遍用方差-协方差法，它的前提假设是资产（或组合）收益率服从正态分布，收益率的均值和标准差可以使用GARCH族模型进行预测。利用正态分布的置信度和与之对应的分位数来计算VaR值[7]。其公式为：

其中，Zα表示不同置信度下的临界值，σt在t+1时期下预测同一天的收益率波动值。

金融数据经常表现出波动性集群，即通常一个大（小）波动后面跟着另一个大（小）波动。这种现象常会导致资产收益率的分布出现尖峰、厚尾的现象[8]。条件异方差（ARCH）模型可以解释这种现象，GARCH模型为典型的条件异方差模型。1986年Bollerslev建立了GARCH模型[9]。GARCH及其以后产生的扩展模型被称为GARCH模型族，由于金融资产的未知收益对条件方差的不对称影响，GARCH模型又可扩展到TGARCH、EGARCH和PGARCH等模型。GARCH模型的基本形式如下：

其中，α0＞0，α1，…，αp≥0，βj≥0（i=1，2，…，p）

以上模型都是假设条件均值不变的，而有时这种假设不一定总成立，条件均值与波动性存在一定关系，金融资产的收益率与投资风险紧密相关，所以Engle等人提出了GARCH-in-Mean模型，基本形式如下[10]：

其中，γ代表了股票收益率和风险之间的关系。正常情况下，γ值为正，收益率和风险正向变化，负γ值情形较少。

对于分布问题，一般标准的GARCH族模型残差εt=qt·σt中的qt（独立同分布的随机变量）为正态分布，但股票收益普遍具有厚尾特征，t分布、GED分布（广义误差分布）或许能更好地将其描述[11]。

t分布的概率密度函数为：

其中，Γ为Gamma函数，υ为自由度，当υ趋于无穷，t分布的概率密度函数逐渐收敛于正态分布。

GED分布的概率密度函数为：

在GED分布中，自由度υ=2时，此分布为正态分布；υ＜2时，此分布呈现出厚尾特征；反之瘦尾特性。

三、实证分析

（一）数据选取及基本描述性统计

本文选取中国人寿、中国平安和中国太保三家保险公司的股票每日收盘价（Pt）作为原始数据，以2015年7月27日到2018年4月27日作为观察期间，同时剔除了没有交易的交易日后，样本容量为672×3=2016个，样本数据均来源于网易财经。为消除数据本身的异方差性，对数据进行对数化处理，使用其日收益率（rt）作为研究对象。定义如下：

经上述处理后的三只保险股的日收益率走势（见图1），我们可以明显观察出，每只股的收益波动率均在零值上下波动，且其波动频率存在显著的聚集性。

图1 三只保险股波动率

表1 日收益率变量统计指标

由表1可看出，三只股票的峰度均大于正态分布的峰度值（K=3），与正态分布相比，显示出尖峰特征。中国人寿的偏度大于0，呈现出右拖尾（高频数在左侧），序列遵循正偏态分布；中国平安与中国太保呈现出一定的左拖尾性，遵循负偏态分布。JB统计量远大于0，三家公司的股价日收益率不服从正态分布，对此进行下一步检验。

对各日收益率数据进行平稳性检验，采用ADF检验法，发现各组序列t值的统计量均小于5%的置信度水平下的值，则不存在单位根，各组均为平稳序列。观察各股票日收益率的线形图（图1）得知，它们具有明显的波动性集群现象。由表2可知，在5%的置信度水平下拒绝原假设，模型残差序列存在异方差性。序列存在ARCH效应，同时，模型残差的平方具有自相关性。

表2 ARCH-LM检验

（二）GARCH族模型的建立

根据上述检验，建立 GARCH（p，q）族模型，从AIC、SC准则和似然值的比较来看 GARCH（1，1）类能更好地描述股票日收益率序列，本文三只股票GARCH族模型的阶数均选择（1，1），假设残差服从正态分布、t分布、GED分布，通过对三种残差分布下的GARCH类模型分析比较，发现t分布下的GARCH类模型能更好地拟合中国人寿股票收益率，模型效果较好；中国平安和中国太保更适应GED分布下的GARCH类模型。如表3、表4、表5 所示，其中 α0，α1，β1，φ1，δ，代表模型方程中的系数，γ是主模型中加入条件标准差后的系数。

表3 中国人寿股收益率的GARCH类模型的估计结果

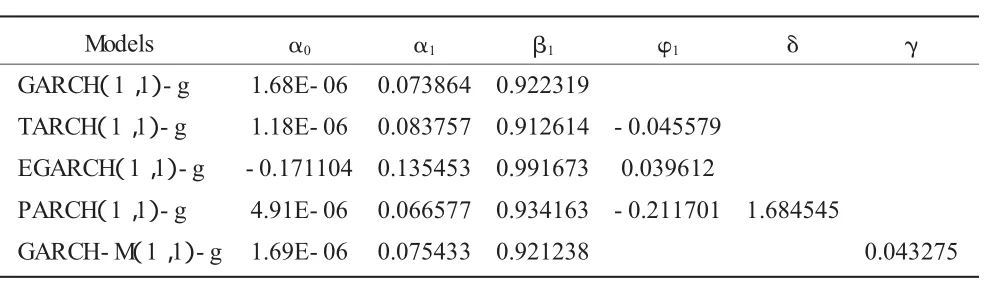
表4 中国平安股收益率的GARCH类模型的估计结果

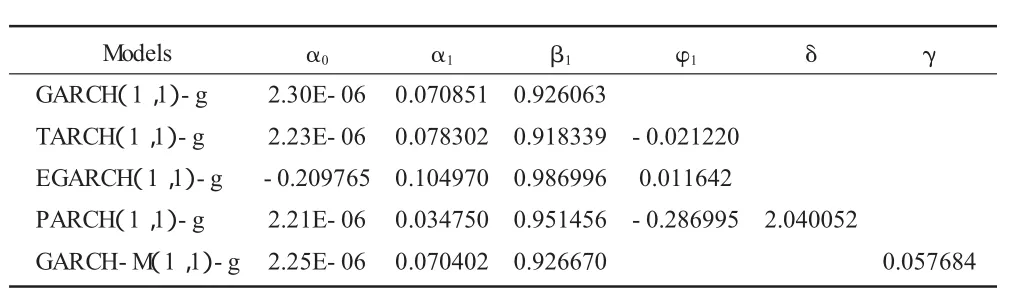
表5 中国太保股收益率的GARCH类模型的估计结果

观察表3、表4、表5，发现三家公司股票收益率的各类GARCH模型的估计结果相似：

（1）在 GARCH 模型中，α0＞0，α1＞0，β1＞0，α1+β1均小于且接近于1，满足了模型系数条件，系数都显著，说明了GARCH（1，1）过程是平稳的。通过三家上市保险公司的收益率波动相对比发现，中国人寿的α1略高于其他两家公司，一定程度上说明了对于外部冲击，如国家政策、经济形势的改变等，中国人寿保险股票价格波动现象早于另两家保险公司，对外在信息的反应较敏感；而中国太保的β1较其他两家公司要略高，也反映了中国太保在股票价格波动时，对外在市场信息的接受反应能力较弱，股票波动有较长的持续性。

（2）在 TARCH、EGARCH、PARCH 模型中，φ1都不为0，相应的伴随概率都在5%的置信度之上，接受原假设，统计不太显著，说明了三家公司的股票收益率波动性的“杠杆效应”不明显，即人们对利空消息的反应度和对利好消息的反应度差不多，利好消息和利空消息对三家公司的冲击基本是对称的；PARCH模型中的δ≠0，也说明了股市存在一定的信息不对称现象。

（3）在风险报酬波动率模型中，中国平安和中国太保的γ＞0说明这两家公司收益率和风险正向相关，收益存在正的风险溢价，市场上的风险每增加一单位，对中国平安而言，其要求的收益增加0.043 275个单位，而中国人寿中的γ＜0，出现了与常理不符的现象，即风险每增加一单位，收益反而会下降0.036 68个单位。

最后，再次对上述各模型的残差进行异方差LM检验，发现F统计量和LM统计量所对应的P值均大于5%的置信度水平，结果不显著，故不存在显著的异方差现象，消除了ARCH效应。

四、VaR的估计及后续检验

用上述的GARCH族模型估计出条件标准差，根据不同置信度、不同分布计算出各模型的分位数，分别考察在99%和95%的置信度下，不同显著性所带来的影响，带入公式（2），相应的得出VaR序列和一些统计特征，其中中国平安是在t分布下估计出VaR值，中国人寿和中国太保是在GED分布下估计出VaR值，三只保险股的估计结果如表6所示。

由表6可以看出，在相同置信水平下，无论采用何种GARCH类模型，中国人寿保险公司的VaR均值、标准差都比另两家公司的略大些，这说明了中国人寿的股票平均损失更高一些，股票收益率波动更大一些，风险也更大一些。同时，相应于各个公司的五个模型计算出的VaR值相差不大，表明了在样本期内，不同GARCH类模型对预测VaR值无明显区别；对同一模型的不同置信水平发现99%水平下的VaR值普遍高于95%水平下的值，高估了风险。但不同保险公司间存在一定的差别，如在GARCH模型中，在95%的置信水平下，中国人寿股票每天的平均损失不超过4.37%，中国平安的平均损失不超过2.69%。

表6 三只保险股在不同置信水平下VaR的统计参数

对VaR进行后续检验，目的是为了检验风险计量模型的有效性和准确性，采取常用的Kupiec失效率检验，失效率即给定样本中VaR被超越的次数[12]。在此，溢出天数为E，样本数为N，失败率=E/N，Kupiec提出用LR（似然比率）检验。公式为：

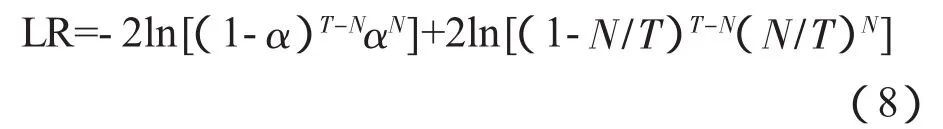
其中，α为置信水平。表7给出测试结果。

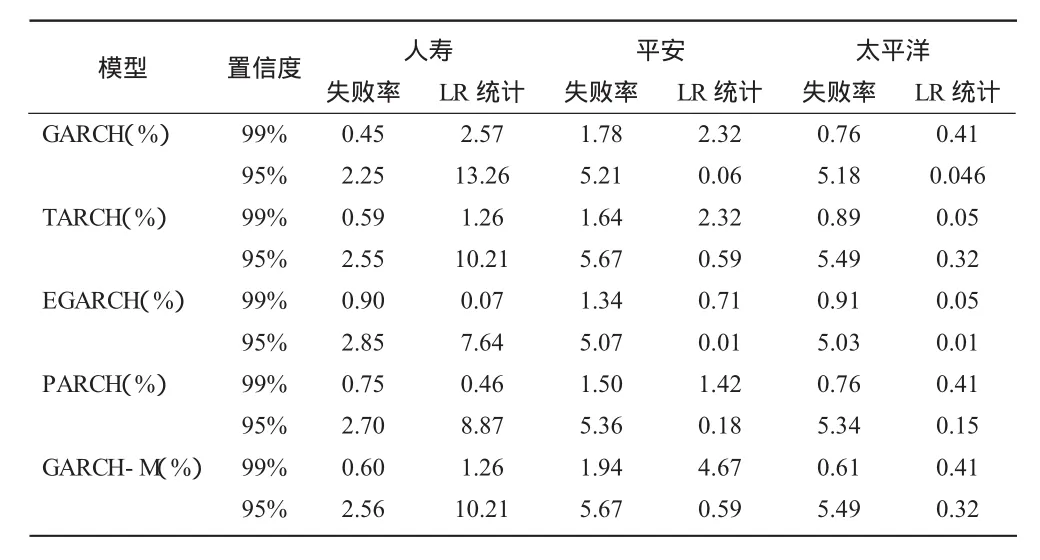
表7 三家公司在不同置信水平下的回测结果

由Kupiec失效率检验的回测结果可知，在99%的置信水平下，中国人寿与中国太保的失败率均低于1%，说明5个模型都略高估了风险，比较5种模型，发现EGARCH模型的失败率最接近显著水平，LR统计量小于临界值6.63，不能拒绝模型，因此在99%置信水平下，中国人寿和中国太保的EGARCH模型对市场风险预测结果最好，如图2、图4所示。中国平安略低估了风险，其中GARCH-M模型的低估程度较大。在95%的水平下，中国人寿严重高估了风险，失败率偏离置信水平，LR统计量大于临界值3.84，中国人寿5个模型的估计过于保守。中国平安和中国太保的失败率略高于5%的置信度，所有模型都略低估了风险，LR统计量都小于临界值，同样的EGARCH模型对这两家公司风险预测结果最好，如图3、图4所示。

图2 中国人寿在EGARCH模型下VaR值与实际收益对比

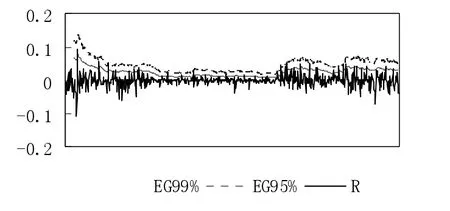
图3 中国平安在EGARCH模型下VaR值与实际收益对比

图4 中国太保在EGARCH模型下VaR值与实际收益对比

五、结论

本文通过对三家上市保险公司的股票收益波动性的研究，发现其收益率序列具有显著的波动聚集性和尖峰厚尾特征。由此建立了GARCH类模型，实证分析表明基于t分布的GARCH类模型能更好地拟合人寿股的收益率；基于GED分布下的GARCH类模型可更好地拟合平安和太保股；它们可以较为准确地刻画收益波动的尖峰厚尾特征、杠杆效应和面临的市场风险。同时计算出VaR值可有效地反映市场风险。基本结论如下：

第一，中国人寿的股票波动风险高于中国平安和中国太保。一方面根据收益率的标准差，中国人寿股的标准差最大；另一方面不管在多少置信水平下，采用何种 GARCH模型，计算出的VaR值的标准差都是中国人寿股最大。但由于中国人寿是基于t分布下研究GARCH类模型，在和另两家公司的比较上或许存在一定的偏差。

第二，收益波动的厚尾特征，外部冲击的不对称性。厚尾性说明了在市场交易中，极端事件发生的概率大于正态分布下的概率，在交易中需注意较少尾部风险，降低极端事件发生概率。将GARCH模型扩展到TGARCH、EGARCH和PGARCH可以很好地捕捉到信息的不对称，如国家政策、经济形势的改变，使得投资者对价格的变化，尤其对价格的下跌十分敏感。

第三，置信水平的不同、分布的不同都对Kupiec检验的结果产生较大的影响。如中国太保在99%的置信度下，略高估了风险；而在95%水平下，略低估了风险。对于中国人寿，在t分布下、在95%的置信水平下，严重高估风险，同时LR统计量大于临界值，在此考虑对中国人寿采用GED分布进行后续测试效果可能更好。

中国人寿与中国太保股投资风险最小，中国平安次之。总的来说，我国保险股相比于市场中的其他板块股的投资风险相对较小，这三只保险股计算Var值与实际损益变化趋势高度吻合，Var-GARCH族模型能有效预测股票的实际风险，可用以测量保险板块的风险，从而为投资者提供参考依据。