基于改进蚁群算法的航站楼滞留旅客疏散路径研究

辜运燕 ，杨建华 ，谢 果 ，石 静

（1.西北工业大学 自动化学院，陕西 西安 710129；2.深圳市机场股份有限公司，广东 深圳 518128）

一、引言

航班大面积延误时大量旅客滞留在航站楼，如果机场、航空公司发布航班取消或是改签，滞留旅客办理取消航班或改签机票后，需到各应急疏散口乘坐交通工具离开，此时合理规划疏散路径十分重要[1]。现阶段滞留旅客疏散路径往往根据旅客所属的航空公司这单一因素进行划分，通过实践发现该方式很多时候会导致单个疏散口异常拥堵，而其他疏散口并没有实质作用。由于航站楼滞留旅客应急疏散路径涉及旅客路径控制、机票退改签、行李提取、合适出口选择等多方面，因此利用科学的方法，建立合理的疏散模型，对航站楼应急路径规划有着重要的作用。

国内外已经有许多学者研究公共场所人群应急疏散等问题，很多研究是对疏散人群行为进行仿真，如社会力模型Anylogic、三维场景建模等[2-3]，这些研究主要从人群数量、疏散速度、疏散时间等方面找出影响因素并提出改进措施。将蚁群算法加以改进用于模拟大型场所人群疏散也有人进行研究[4]，但这些研究很少结合航站楼管理特点，利用蚁群算法针对民航航站楼滞留旅客疏散路径研究的成果较少。根据民航现场保障经验，从复杂系统脆性特性出发，对传统蚁群算法加以改进，剖析航站楼滞留人员应急疏散路径选择问题，研究航站楼滞留旅客疏散路径规划方法，给出民航航站楼滞留旅客疏散管理工作新思路。

二、航站楼应急疏散系统的脆性

（一）复杂系统的脆性

脆性：脆性是复杂系统的固有属性，一个复杂系统在某些外部因素干扰作用下部分子系统会发生崩溃，与它密切联系子系统也会受其影响发生崩溃，同时系统内其他的子系统也会相继受影响，最终可能导致整个系统发生崩溃，如果系统规模越大，子系统之间关系越来越复杂，这种崩溃的性质就越来越突出[5-6]。

系统崩溃[7]：设某一复杂系统有输入xi（i=1，2，…，m），输出为yj（j=1，2，…，n），当∀1≤j≤n，yj=0时，则表示系统为安全状态，该系统输出功能正常，当∃yj=1，1≤j≤n时，则表示系统为崩溃状态，该系统输出功能不正常。对于∀xi[（xi）min，（xi）max]，系统的状态是稳定的；只要∃xi∉[（xi）min，（xi）max]，系统便将出现崩溃趋势。

（二）航站楼应急疏散系统的构成及脆性分析

航站楼应急疏散系统主要由旅客子系统、值机子系统、行李提取子系统、疏散道路子系统、地面交通子系统和管理与控制子系统等组成，每个子系统独立又相互联系、相互作用，具体如图1所示，其中的任意一个子系统运转不畅将影响整个应急疏散系统。

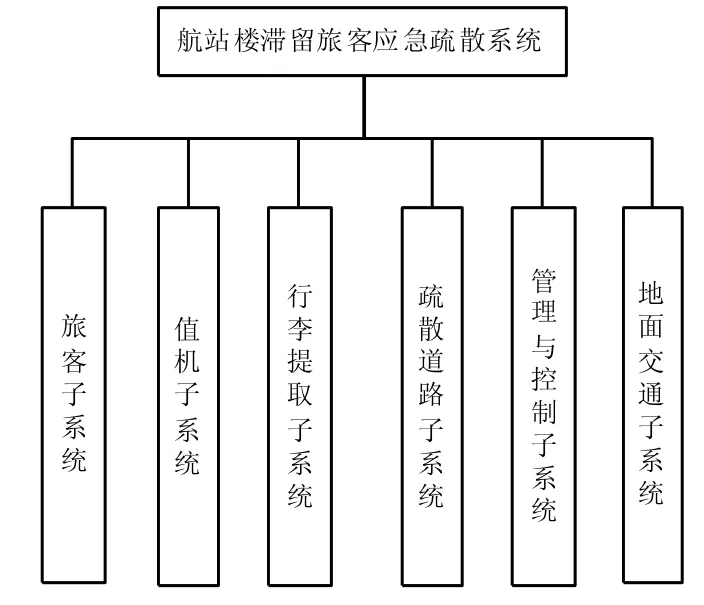
图1 航站楼滞留旅客应急疏散系统构成

航站楼滞留旅客应急疏散系统是一个复杂系统，同时又具有脆性。它包含多个子系统，每个子系统包含多个元素，子系统之间相互影响，有很强的交互性，每个子系统的元素之间也有复杂的关系。当子系统受到不确定因素干扰时，由于子系统之间相互作用，其他子系统也会受到影响，干扰因素不断加大导致子系统相继崩溃，可能导致整个系统崩溃[8]。航站楼滞留旅客疏散系统崩溃表现为航站楼内拥挤不堪、排队时间过长、发生旅客扰乱行为等。

三、航站楼滞留旅客疏散路径分析

各子系统的疏散效率和拥堵程度大小，是决定整个疏散系统能否高效运行的核心。在航站楼滞留旅客应急疏散模型中，根据航站楼旅客疏散的特点，容易引发拥堵的节点列为障碍物点，即为行李提取转盘、值机柜台及最后的交通疏散口，这些节点即为关键节点。每个关键节点所在子系统在一定容量内不会发生拥堵，一旦超过该容量拥堵就会突显，每个关键节点容量大小用拥堵因子表示。当其中一个发生拥堵时，将影响到整个系统的运转程度，机场管理者需要对航站楼内聚集的旅客进行有效疏散，为避免拥堵，引发疏散系统瘫痪，因此找到合适的、高效的疏散路径尤为重要。

根据旅客行李托运的情况，将航站楼滞留旅客疏散路径分为两类：

1.有行李托运退改签旅客疏散路径：行李已经托运的旅客，需前行至航班到达层行李转盘处取回行李，再前行至出发层柜台进行机票退改签，然后根据航空公司安排或旅客自行意愿前行至出口乘坐交通工具。

2.无行李托运退改签旅客疏散路径：未进行行李托运的旅客，只需前行至出发层柜台进行机票退改签，然后根据航空公司安排或旅客自行意愿前行至出口乘坐交通工具。

在航站楼应急疏散流程中，从登机口到各疏散点有一定流程。航站楼疏散流程图如图2所示。

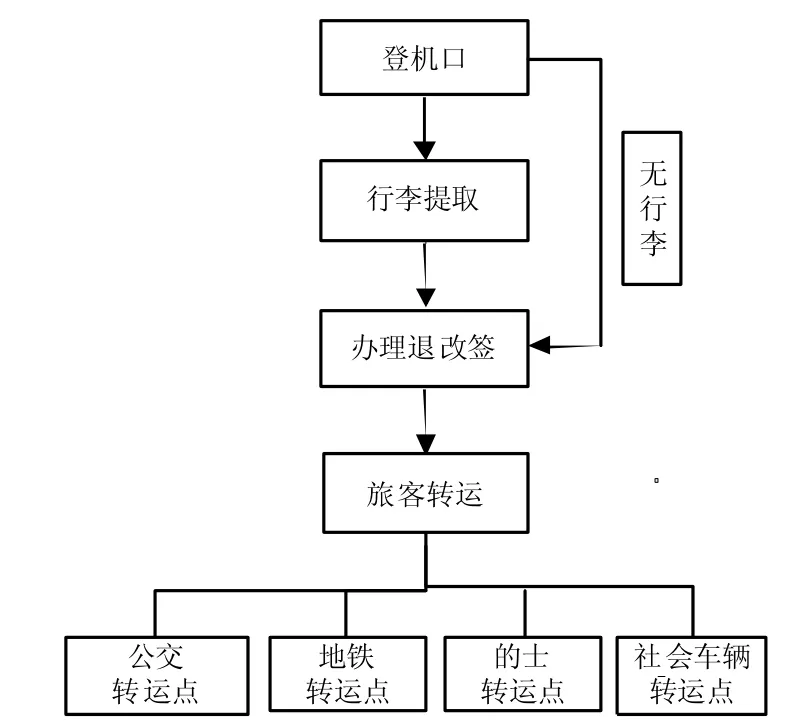
图2 航站楼滞留旅客应急疏散流程图

四、改进蚁群算法在航站楼旅客疏散路径规划中的应用

（一）改进的蚁群算法原理

传统的蚁群算法是在蚂蚁寻求实物的过程中，通过信息素的浓度不断加强或是减少，蚂蚁与蚂蚁之间的交流直接追寻信息浓度进行路径辨识，经过多次选择路径，最终根据信息素浓度的大小蚂蚁寻找到最优路径，然后将食物沿最优路径搬回。传统蚁群算法中，算法初期每个节点的重要性都等同，算法核心在于根据信息素浓度的大小寻找下一个节点，每个节点的信息素浓度因蚂蚁的聚集程度不同而不同。

在利用蚁群算法模拟航站楼滞留旅客疏散路径时，将传统蚁群算法进行改进，改进蚁群算法不仅要考虑该算法是单向有效，蚂蚁不会回到原点，还需考虑复杂系统存在脆性特征，在关键节点设置拥堵阈值，即拥堵因子W（列向量常数）。当关键节点信息素浓度在阈值内，蚂蚁根据信息素浓度选择该节点，当节点信息素浓度大于阈值，该节点发生拥堵，则重新选择新的关键节点。改进蚁群算法与传统蚁群算法的对比如表1所示。

表1 改进蚁群算法和传统蚁群算法的不同点

（二）改进蚁群算法在航站楼应急疏散系统中的应用

在算法的初始时刻，设置拥堵因子W（列向量常数），m个旅客处在登机口s点，首先判断是否有行李，根据判定的结果将每个旅客可能前往的目标编号存放在禁忌表中。此时，各路径上的信息素浓度大小相等，即信息素浓度初始值 τ（i，j）=C（常数）。然后，每个旅客根据路径上实时的信息素浓度和启发式信息独立地选择下一个目标点。第m个旅客从目标点i转移到目标点j的概率pk（i，j），具体公式为[4]：

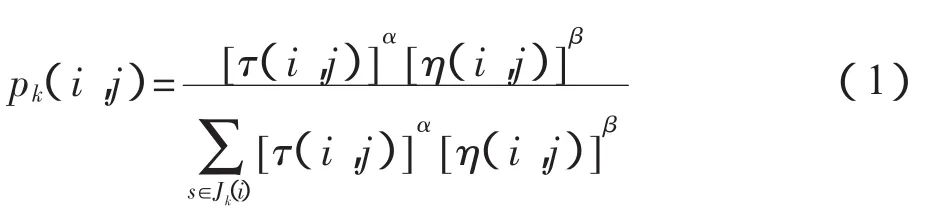
其中：允许第m个旅客未选择的顶点集合为Jk（i）；τ（i，j）为路径 ＜i，j＞ 上的信息素浓度，用一个非常小的正常数作为初值；η（i，j）为启发式信息，又称自启发因子，描述从目标点i到j的期望程度；η（i，j）为能见度；参数 α 为信息素的加权值，主要定义为信息素浓度对疏散路径的相对重要程度，设α＞0；参数β为能见度加权值，主要定义为启发式信息对疏散路径的相对重要程度，设β＞0。

其中 d（i，j）是 i、j两点的距离。

利用判定行走的路线，选取信息素最强的点作为下一步行走的目标，即：

当 τ（i，j）＞W（i，j）时，则该关键节点发生拥堵，重新选择关键节点。其中W（i，j）是航站楼关键节点的拥堵因子。

当m个旅客完成一次行走，每条边上的信息素浓度都会减少，设定变量 ρ，1-ρ（0＜ρ＜1）表示信息素浓度的挥发系数，所有旅客完成一次行走后，信息素值将会更新，具体公式如下：

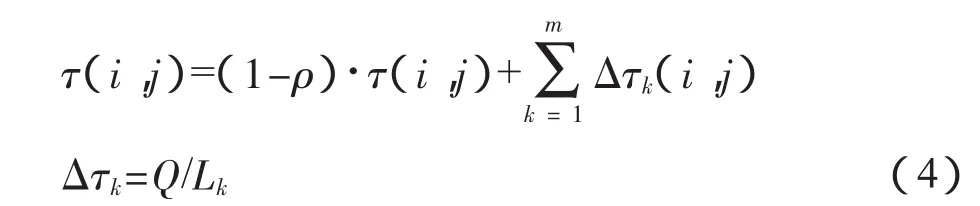
其中：Δτk为信息素浓度变化量。在k个旅客完成一次行走后，计算出旅客行走的距离得到Lk。Q为信息增强系数，一般为一个常量。

五、实例验证

（一）坐标数据获取

利用全站仪对航站楼行李提取转盘、值机柜台、交通疏散口等障碍物地理位置进行测量，获取各障碍物相对位置坐标。

（二）算法步骤

（1）初始化参数，根据航站楼地图数据，确定蚂蚁初始的位置点S、障碍物位置B及出口位置E，并将其数据转化成矩阵，设定信息素浓度τ（i，j）初始值；

（2）将蚂蚁当前的位置添加至禁忌表，开始迭代，蚂蚁走过的位置点添加到禁忌表中；

（3）通过判定信息素浓度大小，确定行走的方向；

（4）每只蚂蚁完成一次行走后，计算每条边上信息素增量；

（5）设置信息素浓度阀值，当信息素浓度高于阈值时，关键节点添加至禁忌表，重新选择关键节点；

（6）完成设置的迭代次数，输出结果。

（三）仿真验证

（1）结合深圳机场航站楼实际情况，以旅客公交转运为例，进行航站楼滞留旅客疏散路径验证。选取深圳机场地服代理的航空公司的应急疏散情况，发生航站楼滞留人员应急疏散时，深圳机场地服代理退改签柜台一般开放4个，行李转盘一般启用2个，共有7个出口，共计7处转运地点。本文将深圳机场航站楼二维图按照比例尺抽象至一个35*35的像素平面图，将行李提取、退改签柜台等视为障碍物，并在图中标记障碍物的相对位置。具体如图3所示。

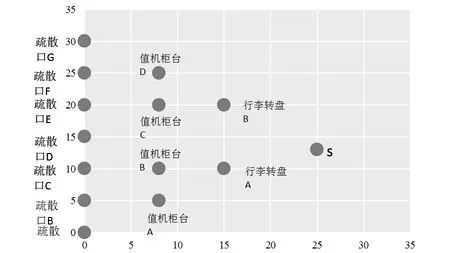
图3 深圳机场航站楼抽象示意图

（2）对疏散口、值机柜台及行李转盘设立拥堵因子即信息素浓度的阀值。阈值设置标准：为保证程序顺利运行，对具有同样使用功能关键节点，设置相同的阈值，同样使用功能节点越多，阈值选择相对较小的常数，反之则选择较大的常数。如深圳机场航站楼疏散口有7处，旅客可选择余度较大，拥堵因子设置为3，相对地，航站楼滞留旅客疏散时行李提取转盘开放2个，选择拥堵因子值为7。具体如表2、表3所示。

表2 疏散口拥堵因子设置表

表3 值机柜台和行李转盘拥堵因子设置表

取200个蚂蚁开始迭代，根据仿真结果得到各个疏散点信息素强度，具体如表4、表5、表6所示。

表4 疏散口信息素浓度最高值

表5 值机柜台信息素浓度最高值

表6 行李转盘信息素浓度最高值

（3）根据仿真结果可以得出，在各个节点信息素浓度小于各节点拥堵因子，在阈值范围内，得出该次应急疏散的最优路径和最不拥堵路径，如表7所示。

表7 最优路径和最不拥堵路径

六、结论

文章从复杂系统的脆性出发，提出改进蚁群算法，在各个关键节点设置拥堵因子，即各关键节点信息素浓度阈值，通过迭代计算各个关键节点信息素的浓度，与拥堵因子相比较，避开拥堵节点，较好地避免了因系统脆性导致系统崩溃的可能性，为后续应急疏散研究提供一定的理论基础。在类似航站楼应急疏散路径选择上，最优路径的选择不仅需要从最短路径考虑，同时还需要考虑系统的脆性，得到的最优路径是一条在保障效率的基础上，避免因为某个节点或子系统拥堵激发整个系统脆性的最优路径。