基因表达式程序设计在宏观经济预测中的应用
鄢靖丰
(许昌学院 信息工程学院,河南 许昌461000)
Gene Expression Programming,简称GEP[1]是葡萄牙科学家C. Ferreira 在2001年提出的一种新的自适应演化算法,它模拟生物界的自然选择和进化机制,具有自组织、自学习等特征,同时还具有优胜劣汰的自然选择、简单的遗传操作、结构与功能的复杂性等特点.它运用遗传算法[2](Genetic Algorithm, GA)和遗传程序设计[3](Genetic Programming, GP)的基本思想,通过生成计算机程序来解决问题,既吸收了GA和GP的优点:GA个体的固定长度线性串编码,容易进行遗传操作;GP个体的非线性树型表示,可以用来解决复杂的问题.同时又克服了GA和GP的缺点:GA只能解决一些简单问题;而GP过于复杂,不利于进行遗传操作.在GEP中,个体首先被表示成具有固定长度的线性串K-表达式,在计算的时候把K-表达式转换成表达式树.由于GEP利用树来表示计算机程序,因此,可以通过自动生成计算机程序来解决许多问题,如预测、分类、符号回归和图像处理等.
1 GEP算法思路框架与实现过程
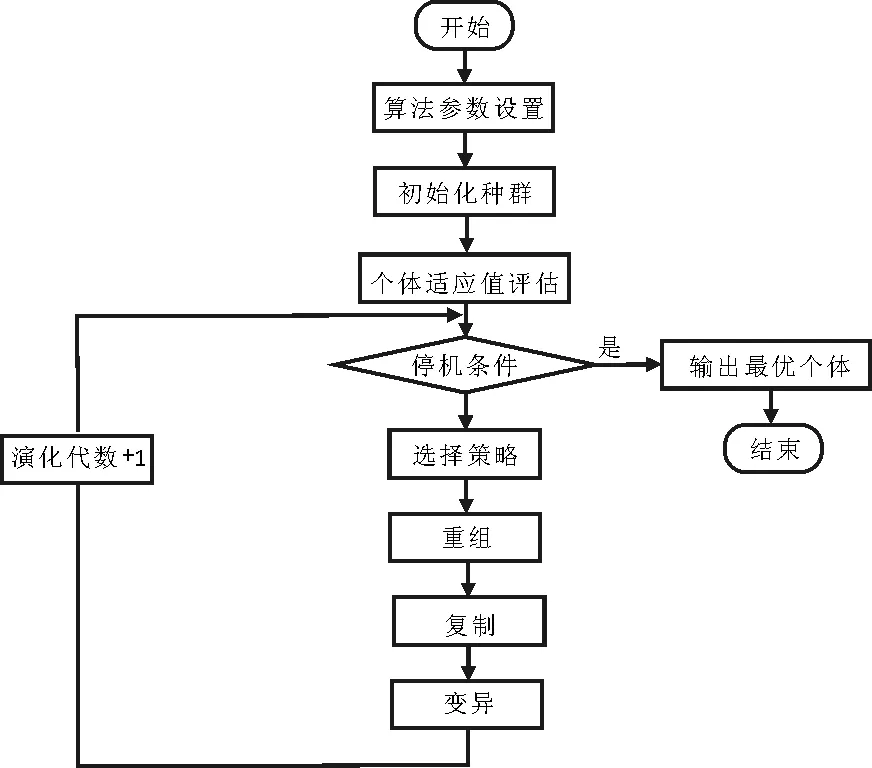
图1 算法流程图
GEP求解函数优化与建模问题主要包括GEP个体编码及表示、适应度函数设计、常数创建以及GEP的遗传操作等,算法求解一般问题的思路框架如图1所示.
1.1 算法编码方案
在GEP中,个体是由一个或多个基因组成.基因是由头部和尾部组成,其中头部符号可以从函数集和终止符集中随机选取(其中第一个符号只从函数集中选取);尾部符号只能从终止符集中选取.如果基因的头部长度为h,则尾部长度t可由公式(1)计算得到,
t=h*(n-1)+1 ,
(1)
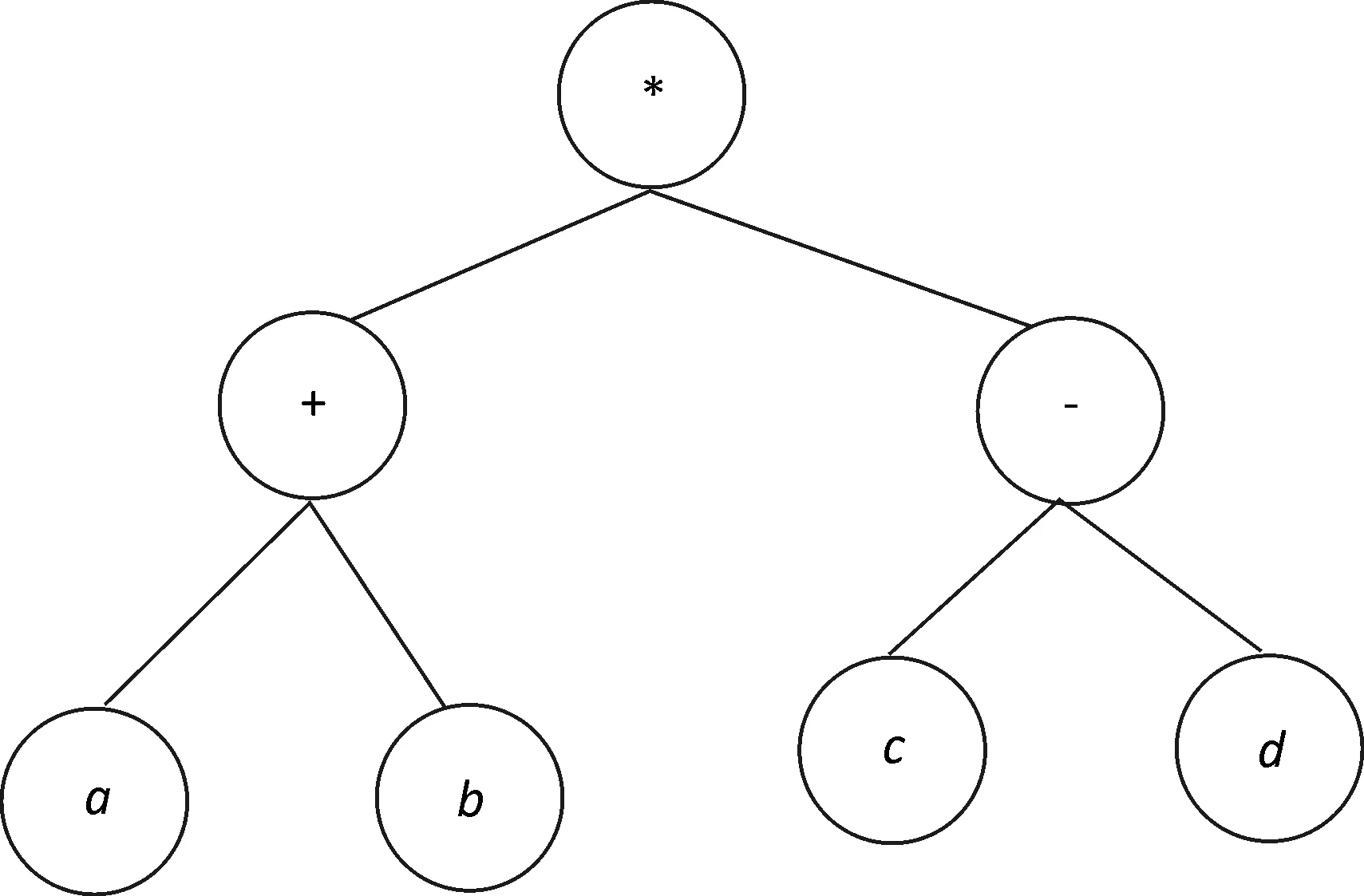
图2 基因表达树
其中,n表示在函数集中变量数最多函数参数个数.由于尾部与头部所具有的特殊关系,必须保证,基因在遗传演化过程中,都不能产生无效个体,即GEP中良性染色体集合在遗传操作下是封闭的[4].将基因内的元素进行编码设计成为K-express,将K-express按照一定规则进行解码构成一个表达树,所以GEP算法的编码具有2种特性,即表现型与基因型,这与传统的GP编程有所不同,这正是GEP的优势之所在,基因表达树的构建树过程如图2所示,构造方法按照中序遍历算法访问,对应基因序列表达式为(a+b)*(c-d).
1.2 适应度函数的设计
在自然界中,个体适应度值就是代表它的繁殖能力,将直接关系到后代的质量与数量.在演化计算中,适应度值是用来区分群体中个体好坏的标准,是算法演化过程的驱动力,是算法进行自然选择的唯一依据[4,5].计算个体适应度值通常会占用较大的计算资源,为此,正确地选择适应度函数对于演化计算顺利进行很关键.
在GEP中,为解决符号回归问题,C. Ferreira提出了两种适应度函数[6,7]:公式(2)是基于绝对误差的公式(3)则是基于相对误差.
(2)
(3)
其中,M是一个常数,表示种群的选择范围,在这个范围内种群开始初始化;C(i,j)表示第i个染色体利用函数关系式在第j个样本中的变量数据所求得的函数值;Tj表示第j个样本包含的实际测量值(比如:有函数表达式z=f(x,y),通过测量得到一个样本(x1,y1,z1),则C(i,j)=f(x1,y1),Tj=z1;Ct表示样本的数目.显然,当C(i,j)=Tj时,适应度函数取得最大值fi=fmax=Ct*M.在实际应用中,当|C(i,j)-Tj|的精度小于或等于0.01时,可以认为它等于0.
1.3 遗传算子的设计
GEP中有多种遗传算子,如复制策略,重组算子,变异算子,插串操作,不同的算子具有不同的功能与作用,利用这些遗传算子进行相关操作,更新种群,维护种群中个体的多样性.下面分别简单介绍.
1.3.1 选择复制算子(replication)
使用某种选择策略对各个体分配选择概率,选择概率及繁殖概率pr,使用转盘来选择个体繁殖,为保证算法的收敛性,我们还采用择优的选择策略[8],即将上代最后的个体保留在当前新的群体中.
1.3.2 变异算子(mutation)
变异是从父体中选择一个染色体(染色体是由一个基因或多个基因组成),再从染色体中选择变异的节点,若选择的节点为头部内的节点,则只能变异为运算符集里面的其它元素;若选择的节点为身部内的节点,则可变异为运算符集和终端集里面的元素;若选择的节点为尾部的节点,则只能变异为终端集里面的元素.对头部和身部的节点变异为其它的节点可以采取类似于转盘赌选择策略的办法[9]来生成变异后的元素,即变异成适应值大的运算符的概率选择应该较大.
1.3.3 移植算子(transposition)
移植是在一个染色体内部操作,在GEP中有三种不同的移植算子[10],IS, RIS ,Gene transposition 在这里我们选择Gene transposition即从染色体中选择一个完整的基因,整体移植到这个染色体另外的一个基因的位置,其它位置的基因依次的向后移动,下面讨论的染色体都是由3 个基因组成的.

012345678012345678012345678*-/aabaab/-q+baaabq+/ababab
把第2 个基因通过Gene transposition 操作到第1 个基因的位置上,其结果
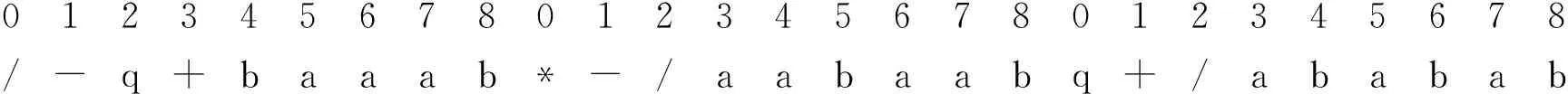
012345678012345678012345678/-q+baaab *-/aabaabq+/ababab
1.3.4 重组算子(recombination)
重组是在不同的染色体间的操作,在GEP中有三种重组算子,单点重组(one-point recombination),两点重组(two-point recombination),基因重组(gene recombination).本算法选择单点重组(one-point recombination),随机选择2 个染色体,然后再随机选择一个重组点,交换以重组点分界地后面地基因片断.
2 算法的改进
由于GEP线性串和表达式树之间的映射关系,使得它可以在问题求解空间无约束的搜索,并且产生有效的程序结构,但是在确定程序的结构后,如果参数选取不当也会导致所建立的系统不稳定.因此, 较好的常数创建对算法的效率与稳定性非常重要.
本文采用由算法本身来创建随机常数,并在程序执行过程中根据适应度函数不断自适应地调整,本文与文献[1]中的常数创建方法不同的是:本文不在基因中引入附加常数域,而是在基因的终结点集中引入符号“?”用来代表临时随机常数,并用一个数组保存随机常数,在译码时,按顺序用数组中的元素依次替换基因中的“?”.对常数的遗传操作只要对数组中的元素进行即可.这样在演化过程中既不会破坏模型的结构又可节约内存资源和简化基因结构,同时也方便进行各种遗传操作.例如有如下一个基因:* ? * * ? + ? a a ? ? a ? a ?,保存随机常数的数组X[10]={0.43, 0.05, 0.576, 0.001, -2.33, 1.178, -0.25, 2.93, 1.33, 0.98}则相应的表达式树和译码后用随机常数替换“?”的表达式树* 0.43 * * 0.05 + 0.576 a a 0.01 -2.33 a 1.178 a -0.25,对常数的杂交操作采用算术杂交如公式(4)所示.
(4)
3 实验数据与结果分析
本文的实验数据来源于Rob Hyndman网站http:∥www-personal.buseco.edu.an/~hyndman.中整理的关于宏观经济预测的数据.该数据是美国纽约San Francisco 1915年到1996年的电话费用数据,数据具体内容请参考网站上的数据. 此数据集中共有984组数据, 本实验中采用数据集中后30组数据作为预测数据, 前面的30组数据均作为训练样本数据.
3.1 实验公共参数设置
算法参数设置如表1所示.
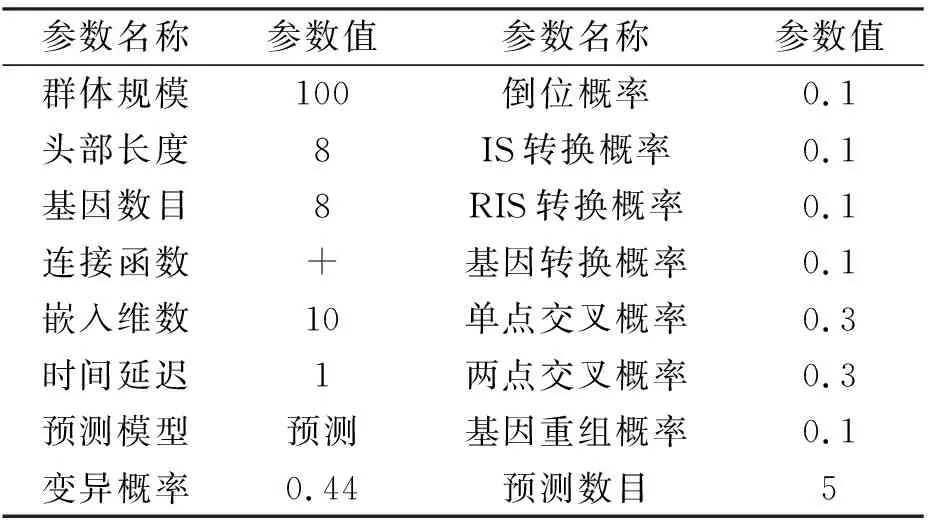
表1 GEP实验公共参数设置
3.2 实验
实验选用函数集F={+, -, *, /},终结点集T={x0,x1,x2,x3,x4,x5,x6,x7,x8,x9},使用随机常数(不完整).实验运行10次找出较好模型为
F=x0/(((x8+x2)*x3)/x8)-x4)+x1)/(x3*x3)+x7+x7/(x2*x2)+(((x6/x3)-(x6-x9))/(x1*x2))*x5+((x0*(x9-x7))-1.203*x8)/x3+0.56*x0/(x1+((x4+x9)-x3)/x9+(x1-x8)/x9 .
(5)
模型(5)的拟合误差按公式(6)计算,
(6)
该模型所得的拟合误差Q=6.987 490,预测误差为0.389 066.拟合结果如图3所示.
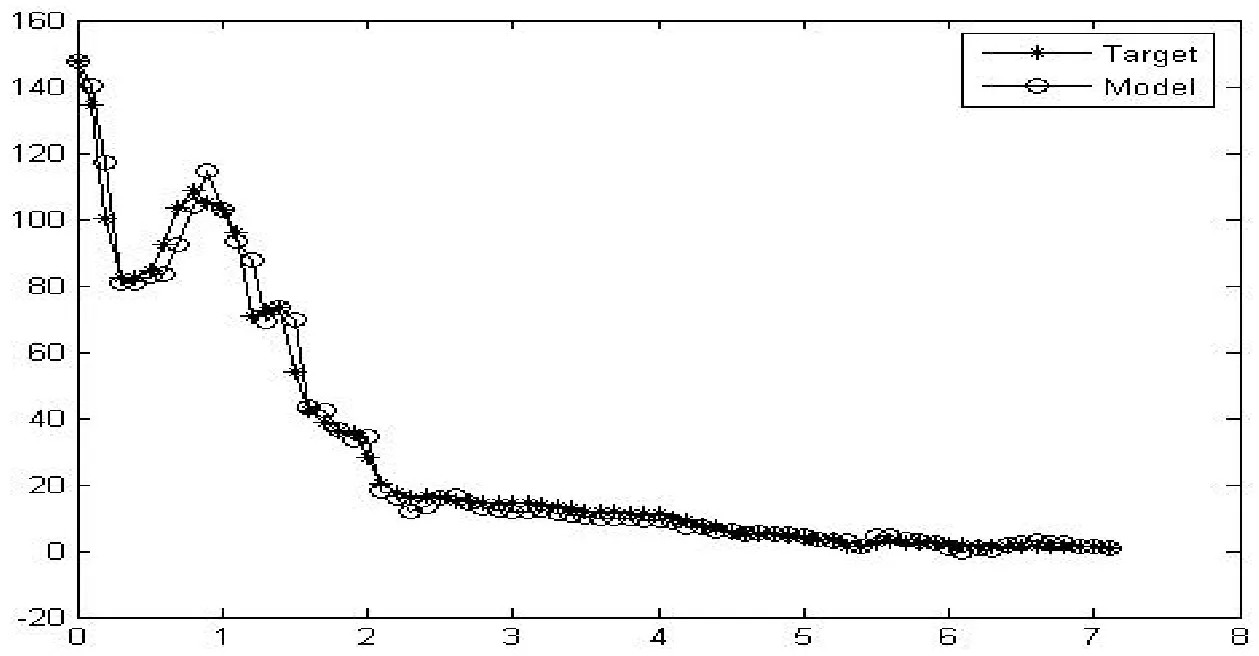
图3 训练数据集预测曲线
3.3 结果分析
从图3可以看出,利用本文的算法能很好地对训练数据进行拟合,而且误差在理想范围内,较好地反映真实情况.通过对以往样本数据进行拟合,本文算法也具有一定效果.
基因表达式程序设计是一种新的自适应进化算法,具有较好的自组织、自适应等特征,文章选用合适的适应度函数, 对常数创建方法进行改进,引入附加常数域,并设计算法的遗传算子与选择策略, 最后把本文算法应用来解决宏观经济的预测问题.结果表明,本文算法能自动找到较好的模型,并能根据所上面所创建的模型进行较为准确的预测.

