Al-Cu合金扩散系数的分子动力学模拟研究
王少刚,刘翠霞,坚增运
(西安工业大学 材料与化工学院,西安 710021)
Al-Cu合金具有高强度,极好的耐热性和加工性能,并且易于焊接,因而广泛应用于航天飞行器轻型装甲以及汽车的零部件等民用领域[1-3].Al-Cu合金扩散系数的研究对于材料的性能有着重大的现实意义[4-6].在以往的液相扩散系数模拟中,通常将液相的扩散系数作为与温度和合金成分无关的常数,这种简化处理会造成定量描述凝固组织结构的准确性降低[7].液相的扩散系数在理论和实际测量中影响因素很多,难度远远高于气体和固体.目前的理论模型还不能对液相扩散系数有较为准确地计算和预测[8-9],在实际测量中也有相当大的难度.当前在研究液相扩散系数时所采用的方法大都基于Miedema模型和Eyring模型,文献[10]创造性地将基于反应速率的过渡态理论应用到液体黏性流动过程,推导出Eyring黏度方程,将wigner-seitz从纯金属推广到二元合金得到Miedema模型来计算生成热.文献[11-13]在两个模型的基础上,通过动力学模拟计算了Al合金的非晶化转变温度,并且通过相场法模拟得到了连续冷却凝固下的微观组织.而在Al合金凝固过程中的原子扩散情况无相关的模拟分析[14-15],因此,本文采用嵌入原子势 (Embedded Atom Method,EAM)对Al0.67Cu0.33凝固过程的扩散系数进行计算机模拟,通过模拟不同初始温度和不同弛豫时间对凝固过程扩散系数的影响,解释凝固过程中扩散的本质,为Al-Cu合金的发展奠定理论基础.
1 实验模型与方法
文中主要以Al0.67Cu0.33合金为例,研究Al-Cu合金凝固过程的扩散系数,采用分子动力学方法并借助大规模原子分子并行模拟器LAMMPS软件进行模拟计算.本次模拟以Al2Cu结构模型为基础,首先建立一个Al2Cu单个晶胞,之后在LAMMPS中X,Y和Z方向分别复制建立15a0×15a0×12b0的模型,原子总数为32 400个,a0,b0为Al2Cu的晶格常数,分别为0.607 nm和0.488 nm,采用周期性边界条件.
分子动力学方法是基于经典牛顿力学建立方程组,对象为分子或者其他微观粒子.在晶体结构模型建立时原子数量越多,模型尺寸数量级越接近宏观尺寸,实验结果越准确,但是受限于当前计算机水平,建立晶体结构模型时选取的原子数目与宏观物质相比显得非常少,这种情况下由于表面原子较多,表面效应会使模拟与实际情况有极大的偏差.解决的办法是在微观的晶体结构模型下采用周期性边界条件,即将体系中的规则原子作为一个立方晶胞,向三维空间复制扩展,达到与宏观实际情况相符的模拟环境.
选择基于EAM势的Al-Cu合金势能函数,在宏观正则(NVT)系综下,设置不同的初始凝固温度,最高初始温度为1 400 K,最低初始温度为950 K,以梯度50 K进行降温,计算Al-Cu合金凝固过程的其扩散系数.其次,设置不同的弛豫时间,在等温等压系综(NPT)中,计算Al-Cu合金凝固过程的均方位移和扩散系数,分析不同弛豫时间对最终扩散系数的影响.
2 结果与分析
物质的扩散系数表示它的扩散能力,是物质的物理性质之一.在LAMMPS所得的数据中并不能直接得到扩散系数,而是通过在运动的某一时刻,所有粒子距离各自初始点的距离的平均值的平方,这被称作均方位移(Mean Square Displacement,MSD).文中采用Einstein法来计算超临Al-Cu合金自扩散系数,在得到MSD后通过Einstein公式求解粒子的自扩散系数.本次模拟是在周期性边界条件下计算均方位移,即原子的位移,实验数据仅仅记录了原子距初始位置的距离,所以试验所得为Al-Cu合金的自扩散系数.
当体系处于固态时,原子排列长程有序,当前位置进行热振动时,原子自由能较低不足以脱离束缚状态,所以均方位移存在上限值.而当体系处于液态时,液态金属温度高,原子自由能大,而且液态金属中存在时隐时现的近程有序的原子集团和大量空穴.由于这些原子自由能大导致原子集团不稳定,原子集团和空穴时而在某一区域消失,时而又在另一区域出现,这种由于原子的布朗运动产生的现象称为结构起伏.而因为液态金属中原子在自由能的驱动下进行结构起伏,所以原子与原来所在位置的距离随时间增大.即液态金属中随着时间的增大原子的均方位移呈线性增长.在凝固过程中,当金属为液态时,均方位移与时间的函数图像上呈线性增长的直线.随着温度降低,液态金属逐渐从短程有序向长程有序转变,这一过程中原子的自由能和扩散能力降低,表现在均方位移与时间函数图像上为增长逐渐趋于平缓的曲线.而当体系完全成为固态时,原子在自身位置振动,此时均方位移与时间函数图像呈水平直线.
均方位移和扩散系数的表达式为
(1)
(2)
其中:Dself为粒子的自扩散系数;N为粒子总数;t为时间;ri(t)和ri(0)分别为粒子在t和t0时刻的位置;<……>为系综平均.将式(1)代入式(2)可以得到自扩散系数和均方位移关系式为
(3)
由式(3)可以得出,当t非常长时,均方位移和扩散系数线性相关,并且根据其斜率可以求得自扩散系数.
2.1 模拟体系的结构变化
径向分布函数(Radial Distribution Function,RFD)是指对于确定的某个粒子的坐标,其他粒子在目标原子周围的分布几率.径向分布函数能有效研究物质的有序性以及描述电子的相关性.在凝固过程中根据径向分布函数来判断合金是否达到结晶状态,在径向分布函数中,波峰意味着出现在原子周围的概率,波峰越高、越尖锐表示在该范围内出现原子的概率越大,这也意味着原子排列有序程度越高,标志着晶体结构已经逐渐形成.图1为不同冷却速率下的径向分布函数.
由图1可以看到,当冷却速率为1.0×1010K·s-1时,第一波峰明显变得高且尖锐,说明此时原子周围第一临近原子非常多,原子排列长程有序,具有很明显的晶体结构特征.当冷却速率为1.0×1014K·s-1时,第一波峰明显很低,此时原子有序很低,具有典型的非晶态特征.随着冷却速率的增大,曲线的峰型逐渐变钝,第二峰逐渐消失,说明此时的体系中原子有序性进一步下降,即同时具有非晶态和晶态的特征.最后第二峰越来越平滑,原子排列短程有序,表现出明显的非晶态.在不同冷却速率下得到的模拟结果,还可以通过对原子结构的直接分析来表征其凝固情况.
图2分别为在五种不同的冷却速率下Al-Cu熔体凝固后的原子结构图及结构分类示意图.在五种不同的冷却速率下凝固得到的原子结构存在很大的差异,从图2可以直观地看到Al-Cu熔体在冷速为1.0×1010K·s-1时发生了结晶.

图1 Al-Cu合金在不同冷速下的径向分布函数
2.2 初始温度对扩散系数的影响
扩散系数的大小主要取决于扩散物质和扩散介质的种类及其温度和压力.在Al-Cu合金凝固的工业生产中,温度是最大的影响因素之一.因此,研究液相凝固的初始温度对凝固过程可能出现的影响有很大的意义,不仅可以降低铸造过程的成本,还可以精确控制其凝固过程.
根据Al-Cu二元相图,Cu原子含量为33%时的熔点为864.15 K,为保证模拟合金完全为液态,模拟过程中液相凝固的初始温度为950~1 400 K,间隔梯度为50 K,模拟系综选择宏观正则系综,弛豫时间相同为400 ps,在冷却速率相同的情况下降至825 K,最终温度大于平均结晶温度814 K.模拟不同初始温度降温过程中MSD的变化规律,如图3所示.
从图3可以看出,随着初始温度的降低,MSD明显降低,说明初始温度和MSD成正相关.当初始温度较高时,MSD值越大,表明温度越高其内部原子在平衡位置震动越剧烈,原子有足够大的驱动力达到平衡位置.随着初始温度的降低,MSD曲线拟合的斜率由1 400 K时的2.19降至1 000 K时的1.25,表明原子运动的驱动力变小,导致其速率变小,而且温度越低越接近凝固温度,原子排列趋于长程有序,所以原子运动所受阻力增加,运动变得困难.而MSD曲线斜率变小,也标志着扩散系数随之变小.

图2 不同冷速下的原子结构及结构类型图

图3 MSD与不同初始温度的关系曲线
图4为不同初始温度下的扩散系数的平均值,由图4可以明显看出,温度越大,扩散系数越大.随着温度的降低,扩散系数不断降低,并且在1 200 K以后保持在较低的稳定值.在1 050 K时出现了扩散系数增大的现象,这与分子动力学计算原子的均方位移有很大关系,由于模拟中原子坐标通过迭代计算得出,反映的是一段时间内的原子坐标位置,与原子的实际运动轨迹具有细微差别,因此,在一定程度出现扩散系数的起伏属正常现象.
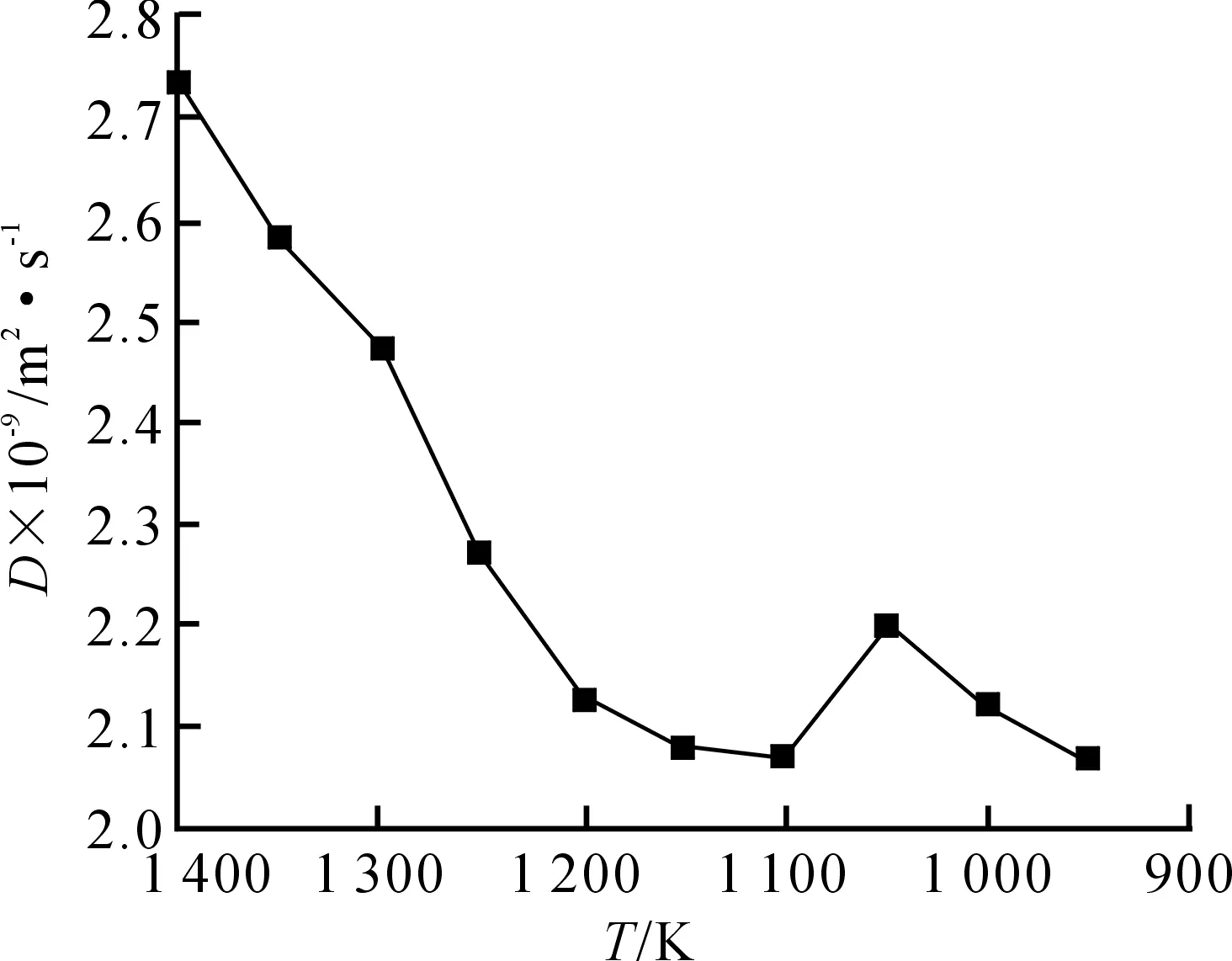
图4 扩散系数与初始温度的关系曲线
图5分别为初始温度为950 K、1 000 K、1 050 K和1 100 K时的原子形态图,由图5可以看出,随着初始温度的增大,原子形态更加趋于无序.总体而言,均方位移和扩散系数均与凝固前的初始温度成正相关.
2.3 弛豫时间对扩散系数的影响
Al-Cu合金凝固的弛豫时间也会影响扩散系数,这是因为凝固前液态原子的状态以及液相原子的聚集状态会直接影响凝固过程,导致扩散系数不同.实验模拟在凝固初始温度为1 400 K时,改变弛豫时间,计算弛豫时间对扩散系数的影响.

图5 不同初始温度的原子形态
图6分别为弛豫时间为4 ps、6 ps、8 ps和10 ps时的MSD,其模拟系综为NVT系综,初始温度均为1 400 K,在冷却速率相同的情况下降至825 K.由图6可以发现,降温初始阶段扩散系数最大,随着降温时间的增加,扩散系数不断变小.随着弛豫时间的增加,原子的扩散能力明显增强.

图6 MSD与弛豫时间关系曲线
图7为扩散系数与弛豫时间关系曲线,由图7可以看出,扩散系数会随着弛豫时间的增大而增大.图8分别为弛豫时间为0.2 ps、2 ps、3 ps和4 ps后降温至825 K时的原子形态.弛豫时间为0.2 ps时,得到的同种原子依然有很多聚集,而弛豫时间为4 ps时,得到的原子明显呈无序状态.弛豫时间的增长会使均方位移和扩散系数显著增大,原子排列愈加趋于无序状态.弛豫时间增长,原子处于高温热振动的时间越长,能够有更大的几率去扩散到平衡位置,原子越来越趋于无序,扩散系数增大.

图7 扩散系数与弛豫时间关系曲线

图8 不同弛豫时间下的原子形态
3 结 论
1) 随着冷却速率的降低,Al-Cu合金原子排列有序性不断升高,由径向分布函数可以看到,其在1.0×1010K·s-1的冷却速率下凝固后具备了明显的晶体结构特征.
2) 初始温度对扩散系数具有直接影响,随着初始温度的降低,扩散系数也随之降低.在最高初始温度1 400 K下,得到Al0.67Cu0.33合金的平均扩散系数为2.73×10-9m2·s-1,在最低初始温度950 K下,平均扩散系数为2.07×10-9m2·s-1.
3) 弛豫时间对扩散系数的影响较为巨大,随着弛豫时间的增加,MSD和扩散系数也随之增加,原子排列趋于无序状态.

