一类带p-Laplacian算子分数阶微分方程边值问题正解的存在性
王文倩, 周文学, 孙 芮
(兰州交通大学 数理学院,兰州 730070)
分数阶微积分在数学上已有很长的发展历史,现如今已在诸多领域得到了广泛应用。[1-6]近年来,对带p-Laplacian算子的整数阶微分方程的研究取得了很大进展,但整数阶微分方程在实际应用上具有一定的局限性,为了解决现实中越来越多的复杂的现象和问题,许多专家和学者开始逐渐深入学习和研究带p-Laplacian算子的分数阶微分方程。[7-12]
2010年,王金华和向红军在文献[13]中用上下解方法证明了边值问题
正解的存在性。其中1<α,γ<2,0 2014年,Ertao Zhi 和Xiping Liu在文献[14]中研究了边值问题 正解的存在性,其中0<ξ1ξ2<1,2<α<3,1<β<α-1<2,0<λ1,λ2<1。 2016年,孔德琼,马德香在文献[15]中讨论了边值问题 正解的存在性,其中λ>0,f:(0,)→(0,+)连续,2<α3,1<β2,α,β为实数。 受到上述文献的启发,文章主要利用Guo-Krasnoselskii不动点定理研究边值问题 (1) 正解的存在性,其中,1<α2,2<β3,α,β是实数,0<ξ,η<1,λ>0,f:(0,)→(0,+)是连续的。 引理1.1[7]假设α>0,若u∈C[0,1]∩L[0,1]有α阶Riemann-Liouville导数,则 其中N为大于或等于α的最小整数。 引理1.2[16]令h∈C[0,1],则边值问题: (2) 存在唯一的解u∈C2[0,1],u(t)可表示为 其中 引理1.3令y:[0,1]→R连续,那么边值问题: (3) 存在唯一解,其中2<β3,β是实数, 其中 证明:由引理1.1可知 由(3)中边界条件可知 因此 引理1.4令h:[0,1]→R连续,那么边值问题: (4) 存在唯一解,其中3<α4,α是实数, 其中 证明:由题意可得 由(4)中边界条件可知 因此 引理1.5令f∈C[0,1],考虑下面边值问题: (5) 证明:由引理1.2,引理1.3和引理1.4可得边值问题的解为 引理1.6[15]当3<α4,2<β3时,函数G(t,s),H(t,τ)的性质为: (1)对任意的τ,s,t∈[0,1],有G(t,s)≥0,H(t,τ)≥0; 引理1.7[16]假若0<η<1,0<ξ<1,h∈C[0,1],则K(t,μ)在[0,1]×[0,1]上连续且有以下的性质: (1)K(t,μ)>0,(t,μ)∈[0,1]×[0,1]; (2)K(1,μ)K(t,μ)K(μ,μ),(t,μ)∈[0,1]×[0,1]; 引理1.8[11,15]φ:R→R为非减奇函数,ψ1,ψ2为非减同胚映射满足: (1)当x,y>0时,存在ψ1(x)φ(y)φ(xy)ψ2(x)φ(y); (2)在(1)成立的条件下,∀x,y∈(0,)时有,φ-1(xφ(y)) 引理1.9算子T:P→P为全连续算子。 可得,Tλu(t)(P)⊂P,也即Tλu(t):P→P为全连续算子。 为了论述方便,给出以下记号: 定理2.1当F=+,f0=0时,存在,若满足条件 F 那么取ε>0,使得对任意λ满足 成立,则边值问题(1)存在正解。 证明:将证明分为两步: f(u)(f0+ε)φ(u), 若u∈P,‖u‖=ρ1,可得 ‖Tλu(t)‖ =ψ-1(λ(f0+ε))M1ρ1ρ1 =‖u‖。 因此,令Ω1={u∈E|‖u‖<ρ1},所以当u∈P∩∂Ω1时,可得 ‖Tλu(t)‖‖u‖。 (6) 第二步,由F可得,存在ρ3>0,使得当u≥ρ3时,有 f(u)≥(F-ε)φ(u)。 若存在u∈P,‖u‖=ρ2=max {2ρ1,4α-1ρ3},则可得: ‖Tλu(t)‖ ≥Tλu(δ) =‖u‖。 因此,令Ω2={u∈E|‖u‖<ρ2},故当u∈P∩∂Ω2时, ‖Tλu(t)‖≥‖u‖。 (7) 定理2.2当f=0,F0=时,有,存在,若满足 那么取ε>0,使得对任意的 成立,则边值问题(1)至少有一个正解。 证明:现将证明分为以下两步: f(u)≥(F0-ε)φ(u)。 若u∈P,‖u‖=ρ1,证明方法同定理2.1中证明的第二步。 令Ω1={u∈E|‖u‖<ρ1},则当u∈P∩∂Ω1时,有 ‖Tλu‖≥‖u‖。 (8) 第二步,根据f可得,存在R1>0,当u>R1时, f(u)(f+ε)φ(u), 根据f是否有界,考虑下面两种情况: 情况一:若f有界,则存在N>0,当u∈(0,)时,f(u)N。 令ρ3=max {2ρ1,φ-1(λN)M1},当u∈P且‖u‖=ρ3时,得: ‖Tλu(t)‖ =‖u‖。 因此,若Ω3={u∈E|‖u‖<ρ3},则当u∈P∩∂Ω3时,有 ‖Tλu‖‖u‖。 (9) 情况二:若f无界,取ρ4>max {2ρ1,R1},使得当0 ‖Tλu(t)‖ =ψ-1(λ(f+ε))M1ρ4ρ4 =‖u‖。 因此,当满足Ω4={u∈E|‖u‖<ρ4}时,有u∈P∩∂Ω4时,有 ‖Tλu‖‖u‖。 (10) 综上所述,令Ω2={u∈E|‖u‖<ρ2=max {ρ3,ρ4}},当u∈P∩∂Ω2时,总可以得到 ‖Tλu‖‖u‖。 (11) 解:通过计算得 M1≈1.17809,M2≈11.7809,f0=0.2,F=100,可以得到F成立,根据定理2.1得,当λ即0.008λ4.244时,此方程存在正解。 文章在阅读大量相关书籍以及诸多学者文献的基础上,探究一类具有p-Laplacian算子的分数阶微分方程边值问题正解的存在性,获得了正解的存在性定理和至少有一个正解的判断根据,最后,通过具体的例子验证了该结论的适用性。1 预备知识
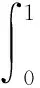
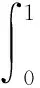
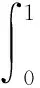
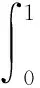
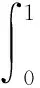
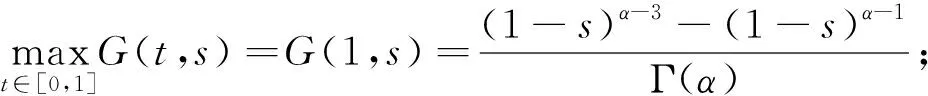
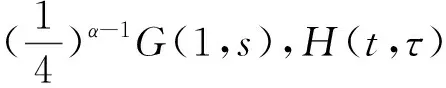
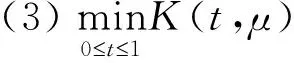
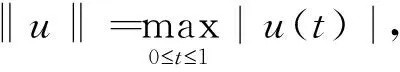
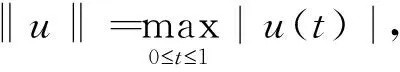
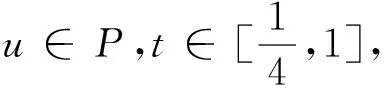
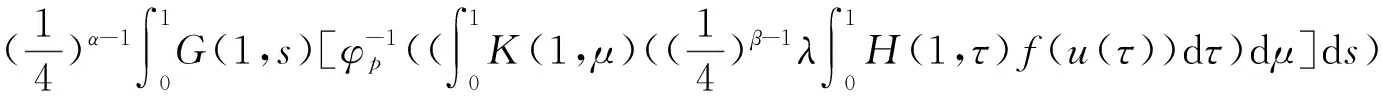
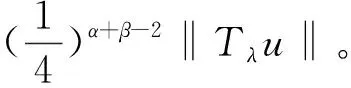
2 主要成果
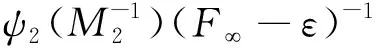
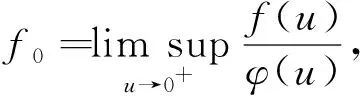
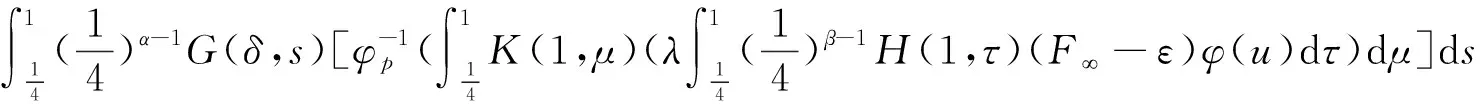
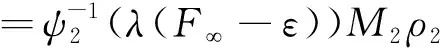
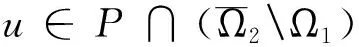
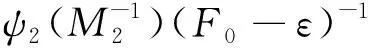
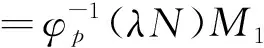
3 举 例
3.1 考虑分数阶微分方程边值问题
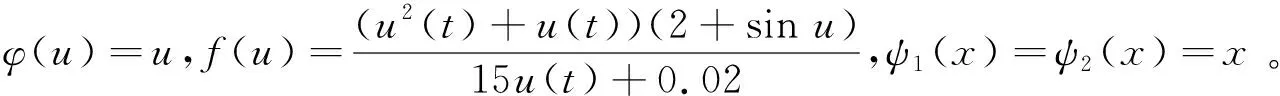
4 小 结

