一种覆盖行为独立性的Prime测试路径生成技术

刘秀青 杜军威 李彦霖

（青岛科技大学信息科学技术学院 青岛 266061）

1 引言

基于图论的软件行为分析是常用测试分析方法［1］，不同层面的软件行为可以抽象建模为各类图［2］，如控制流图、数据流图、系统调用图、用例图、活动图等，因而软件行为分析都可以抽象为基于图结构特征的分析［2～3］，如每个瞬间软件行为可以表现为状态空间的某些状态组合、软件每次执行可以抽象为图的一个路径等。但每个状态和变迁的正确性并不能表示其系统行为的正确，在一些安全关键系统或信息安全系统的行为分析中，每个状态或变迁［4］安全并不能表示系统行为的安全性，如列车控制系统中未通过安全状态检测的移动授权行为；并发系统中时序交替行为约束等。考虑到图的结构特征，基于图的分析可以表现为基于图的不同结构覆盖的分析［1～3］，如：点覆盖、边覆盖、边对覆盖和指定路径覆盖分别考虑图的不同结构特征，而产生覆盖这些结构的测试路径则可以检测状态空间的任意状态、任意变迁，任意连续变迁对、及包含某个特征行为的行为分析与检测。因此，软件行为分析可以抽象为基于图论特征覆盖［2～3］的测试路径生成问题，同时测试路径生成需要考虑一定的代价［5～6］和覆盖特征。

由于存在环路，基于图的全路径分析难以实际实现。目前基于图的路径分析主要包含基本路径分析技术［1］，指定次数的环路覆盖分析技术［7］，Prime路径分析技术［2，9］等。McCabe最早提出图的基本路径的含义［1］，虽然基本路径的组合可以表达任意路径，但这并不能证明基本路径行为正确则任意路径行为是正确的，且无法检测环路中连续变迁关联引发的行为缺陷问题。其实基本路径更关心每次判定节点改变对系统的某条路径的影响，而无法更多的检测关联路径。Paul提出基于Prime路径覆盖技术［2］可以测试非环路的连续变迁覆盖的测试问题，由于缺乏对测试路径的质量的评价标准，覆盖Prime路径的测试路径生成则忽视路径独立性影响问题。Li Nan提出了最小代价测试路径问题［5～6］（MCTP），以节点更少，测试路径更少，每条测试路径覆盖的测试需求更少，测试路径更短为覆盖目标进行测试路径生成，然这些目标本身是相互矛盾的，在路径数目、路径长度、路径覆盖比等因素制约下难以生成可行路径或存在组合路径庞大等问题。本文提出一种兼顾路径独立性与Prime路径覆盖的测试路径生成方法，既考虑路径独立性组合问题又考虑连续变迁覆盖问题，在保证覆盖充分性的同时，使得测试路径数和总测试路径长度在可测性前题下保持在合理的范围，从而保证测试覆盖度的前提下测试路径优化。

2 基于图结构覆盖的测试基本理论

基于图结构特征的测试问题主要包括如下步骤：选择一种测试覆盖性准则，生成满足符合测试准则的测试需求，进一步生成满足覆盖需求的测试路径，产生驱动测试路径执行的测试数据［8］。面向点、边、边对、路径等测试覆盖准则产生的每一条测试路径都是系统的一次执行，而系统的执行需要有测试数据驱动，本文考虑结构覆盖分析的测试路径生成，忽略驱动测试路径执行的测试数据，从而能够从结构本质进行行为分析，本文主要包含的基本理论如下：

定义 1 路径［8～9］的相关定义：图 G=(V，E，Vs，Ve)，其中V是所有节点的集合，E是所有边的集合E={(vi，vj)|vi，vj∈ V}，Vs为图的始点集合，Ve为图的终点集合。该图的路径表示节点或边的序列，表示为 p=v1v2…vm，其中vi∈V ，(vi，vi+1)∈E(1≤i≤m)。定义Node（p）为路径p的节点集合，Edge（p）为路径p的所有边的集合，SubPath（p）为p的子路径集合；定义Path（G）为图G产生的所有路径。

定义2 路径的独立性：基于图G=(V，E，Vs，Ve)的一个路径集合 P={p1，p2，…，pm}，如果同时满足如下两条，则该路径集合的路径是满足独立性：

即，如果一个路径集合中的路径都不是该集合的其他路径的线性组合，且图中的任意一条路径是该组路径集合的线性组合，则该组路径满足独立性。

定义3 基本路径：目前文献中还没有基本路径的形式化定义，一般给出的非形式化的定义是：每次产生的基本路径应该包含不同于已存基本路径的一条新边［1］。

引理1 基本路径集合是满足路径独立性的［1］。

基本路径集合应是不能够相互表达，但可以表达为任意路径的线性组合。基本路径度量和生成算法比较著名的是McCabe提出的圈复杂度计量法［7］，即图的基本路径数量等于图的圈复杂度数。给定一图G，圈复杂度V（G）有三种计算公式：1）V（G）=e-n+2p（e代表图的边数，n是图的节点数，p为图中的连通数），2）V（G）=P+1（其中P为判断节点的个数，如果图为控制流图），3）V（G）= 封闭区域数（图的内、外封闭区域）。然而，基本路径的定义并没有约定生成算法，如果仅从每次生成的路径包含新边的角度，并不能证明生成的路径集合是基本路径。如图1所示，生成的路径集合 P={v0，v1，v3，v4，v6;v0，v2，v3，v5，v6}，因不存在新的边的路径，但该路径的数目为2并不等于圈复杂度数3。仅仅这两条测试路径并不能测试所有的判定条件组合，不能满足所有的测试需求。基本路径在生成的过程中遵循每次只更改路径中的一个判定节点的原则，能够包含所有的独立路径，较大限度地做到充分测试的同时避免了不必要的冗余。

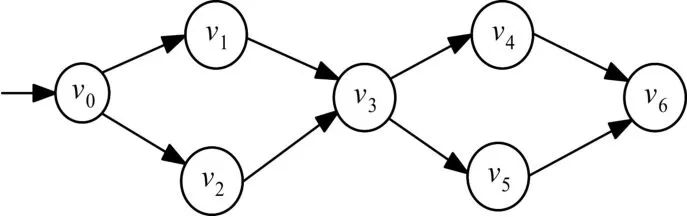
图1 单输入单输出图

引理2 在基本路径生成过程中，一条新路径是基本路径，当且仅当其包含的一个判定节点产生新的一次判定取值且不存在其包含的判定节点产生超过2次新的取值。

证明：生成的一条新路径中，产生一个新的判定取值，则一定产生一条新边，满足定义4的基本路径定义，同时不会产生某个判定的新的两次以上取值，则能够表现每个判定节点的独立性影响作用。该引理不仅能够说明基本路径的本质含义，同时也给基本路径生成算法提供支持。

按照引理2，图1产生的基本路径集合为P={v0， v1， v3， v4， v6;v0， v2， v3， v5， v6;v0， v2， v3， v5， v6} 。

定义 4 Prime路径：图 G=(V，E，Vs，Ve)的一条路径 p=v1，v2，…，vm，如果 1＜i≠j＜m ，vi≠vj，则称为 p 为简单路径［2，10］，如果不存在简单路径 q ，使 p∈SubPath(q)，p为Prime路径。即简单路径就是一条仅可能存在开始节点和终止节点相同外，没有任何节点出现超过一次，也就是说简单路径没有内部环。Prime路径是最长的简单路径，它不会为其它简单路径的子路径。

定义 5 测试路径［2］：给定图 G=(V，E，Vs，Ve)的测试需求集合TR，任意tr∈TR，存在一条路径p=v1，v2，…，vm， v1∈Vs， ∧vm∈Vs，tr∈SubPath(p)。即测试路径是从某个起始节点开始，终止于某个结束节点的一条路径，路径长度允许为0。测试路径代表了测试用例的执行轨迹，一些测试路径可以被很多测试数据执行，也可能是语义不可达的路径，而无法存在测试数据执行。

3 一种覆盖行为独立性的Prime测试路径生成技术

目前存在的面向节点、边、边对、Prime路径等覆盖的测试路径生成技术，或考虑以较少的代价将测试需求目标覆盖，或考虑测试路径的可行性问题，较少考虑测试路径之间与其分布的合理性。

基于Prime路径的测试路径生成技术目前常用两种方法，其一采用将Prime路径之间的链接关系转换为一种流图网络（Flow network）［10］，通过求面向流图节点覆盖路径生成技术产生覆盖Prime路径的测试路径生成技术；其二采用超串（Superstring）生成技术［5，6，9］，采用启发式算法逐层合并 Prime路径，最后形成覆盖Prime路径的测试路径。上述两种方法可以生成面向Prime路径覆盖的测试路径，同时也可以生成总路径长度最小的测试路径集合。但这些生成算法都忽略了路径之间的独立性问题。

根据Prime路径的定义，考虑到图中包含环路，根据Prime路径的起点和终点类型，s代表开始节点，t表示终止节点，c表示环中的节点，将Prime路径分为如下几种类型：1）s→c，这类Prime路径是从开始节点到环内的Prime路径；2）c→t，这类Prime路径是从环内到终止节点的Prime路径；3）s→t，这类Prime路径是从开始节点到终止节点的Prime路径；4）c→c′（c′是不同于c的环），这类Prime路径是从一个环内到另一个环内的Prime路径；5）c→c，是一个自环路径。按照Prime路径类型，选择一种覆盖策略依此覆盖s→c、c→c、c→c′、c→t及 s→t这5类Prime路径类型，生成满足路径独立性的测试路径集合。

满足独立性需求的的Prime路径测试路径的生成策略及算法（IndPriTestPath Algorithm）如下：

Step 1 首先选择s→t类型的Prime路径，这些Prime路径本身也是测试路径，将这些Prime路径加入到完成路径集合和待生成的测试路径集合中，同时将选择的Prime路径标记已覆盖；

Step 2 从完成路径集合中选择一条路径，采用逆向搜索，查找是否存在没有被完全覆盖的判定节点，若存在，执行Step 3，若不存在，说明该测试路径的判定节点均已搜索完，选择下一条测试路径，重复step 2，如果完成路径集合中所有的Prime路径都已搜索完毕，执行Step 5；

Step 3 选取该判定节点的一条新边，以该新边为结尾的路径，按照超串匹配规则选择c→c′或c→t两种类型的Prime路径进行扩展：

如果是c→t类型，则产生新的一条测试路径加入到测试路径集合中，同时标记该Prime路径，转到Step 4；

如果是c→c′类型，则判定该条路径中是否存在一个判定节点同时出现两次新值，如果存在则舍弃该条路径，继续选择新的Prime路径，重复Step 3

Step 4 继续逆向搜寻该路径，如果仍有判定节点存在新的取值，重复执行Step 2。

Step 5 如果仍存在Prime路径未覆盖，则该Prime路径为环路，从测试路径集合中选择一条包含该环起始节点n的最短路径p，用该Prime路径替换

测试路径中的节点n生成新的测试路径 p′，并删除原测试路径p；如果不存在Prime路径未覆盖，则结束。

引理3 无自环有向图中，满足Prime路径覆盖的测试用例集合能够覆盖图中的每个环路零次和两次。

证明：首先证明满足Prime路径覆盖的测试用例集合能够包含每个环路的零次和两次的执行序列。1）假设，测试用例集合中存在一个环没有被包含，考虑一般性环路设该路径为 ai，ai+1，ai+2…ai+k，ai+k+1，ai=ak，零次循环表示测试用例需要覆盖aiak+1的动作序列，即不存在某个测试用例覆盖aiak+1，又ai=ak，则说明不存在一条路径包含akak+1，也不存在路径ak-1akak+1，但是ak-1akak+1是一条从环内到环外的路径，被Prime路径包含在内，因此该假设不成立。2）对于图中的环而言，每个环都是一个Prime路径，因此满足Prime路径覆盖的测试用例集合一定包含图中的所有环。3）考虑 一 般 性 环 路 ，设 该 路 径 为 ai，ai+1，ai+2…ai+k，ai+k+1，ai=ak，对于环 ai，ai+1，ai+2…ak，肯定在另外一个环 ai+j…ak，ai+1…ai+j，ai=ak，根据 Prime路径覆盖准则，ai+j…ak，ai+1…ai+j肯定被覆盖一次，但到 ai+j肯定经过 ai，环 ai+j…ak，ai+1…ai+j中包含ai，最后环 ai+j…ak，ai+1…ai+j的最后一个节点 ai+j在环内，Prime路径覆盖包含环内到环外的路径，肯定也经过ai，因此Prime路径覆盖包含每个环路两次。

无自环的Prime路径测试可以满足图中的节点覆盖、边覆盖和边对覆盖，能够充分保证测试的充分性，但却无法保证路径的独立可行性。

引理4 所有s→t类型的Prime路径都是满足独立性的基本路径。

证明：设 p=v1，v2，…，vm为任意一条 s→ t类型的Prime路径，且 v1∈Vs∧vm∈Ve，所以p也为一条测试路径。因为p为简单路径，则 vi≠vj(1＜i≠j＜m)。即除首尾两个节点外，其它节点不存在重复，也就是每个判定节点只有一次取值，所以p是满足独立性的基本路径。

定理1 一条基本路径从起始节点到终止节点一定可以分解为一条或几条Prime路径的组合。

证明：假设存在一条基本路径 v1，v2…vt，v1为开始节点，vf为终止节点，该基本路径分为有环和无环两种情况。1）基本路径中不存在环路：根据Prime路径的定义可知，这条基本路径也是Prime路径 ；2）基 本 路 径 中 存 在 环 路 ，即 v1，v2…vi，vi+1，…vj-1，vj，…vt，其中 vi=vj：根据超串问题［5～6］，可以将该路径分解 v1，v2…vj-1以及 vi+1…vt两条路径，根据Prime路径的定义可知，这两条路径均是Prime路径，即该基本路径可以分解为两条Prime路径的组合。由此可见，一条基本路径从开始节点到终止节点一定可以分解为一条或几条Prime路径的组合。

定理2 采用算法1生成的测试路径集合，其能够覆盖所有Prime路径且满足每个判定独立影响至少1条路径。

该定理易通过算法的执行过程得证。首先算法终止的条件是所有的Prime路径都会被包含，所有生成的测试路径集合满足Prime路径覆盖。根据Prime路径的合成策略，下面三类扩展方案均满足判定节点的独立影响。

1）算法选用的起始路径为s→t类型的路径，该类路径对每个判定节点只有一次取值，其后采用启发式算法选择其它Prime路径，启发式的目标是a）优先选择c→t类型的路径，其次选择c→c′类型路径，能够快速到终止节点，以期获得较短的路径；b）每次新增加的Prime路径与原来构成的测试路径，其判定节点不允许出现两条新边，以期获得每个判定的独立影响；

2）对s→c类型的路径也是采用1）Prime路径的扩展策略；

3）对c→c类型的路径，在最短包含环路节点的Prime路径基础上进行扩展，以期使环路影响较短的路径，从而也只产生一次判定节点的改变。

通过上面分析，容易看出定理2得证。

4 实例分析

采用文献［5］的例子，对图2的自动投币售货机FSM图进行分析。该FSM包括9个变迁和3个事件，这三个事件分别为“AddChoc”，“Coin”和“GetChoc”，箭头代表事件触发后的转换。该FSM由4个状态组成：1，2，3，4。状态1是初始状态，状态4为终止状态。状态1表示货币等于0且巧克力的数量是0；状态2表示货币大于0但巧克力的数量等于0；状态4表示货币和巧克力都大于0；状态3表示货币等于0巧克力数量大于零。相应的状态表示顾客投币和服务人员放入巧克力的状态转换。

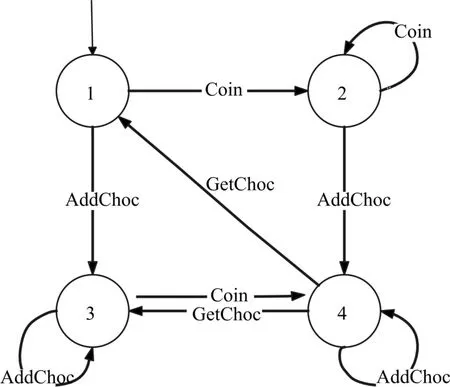
图2 一种自动售货机的FSM

为了测试该自动售货机的行为，主要分析面向判定节点的独立性影响和连续变迁的覆盖问题，采用文献［2］的算法求得的图2的Prime路径集合如表1所示。

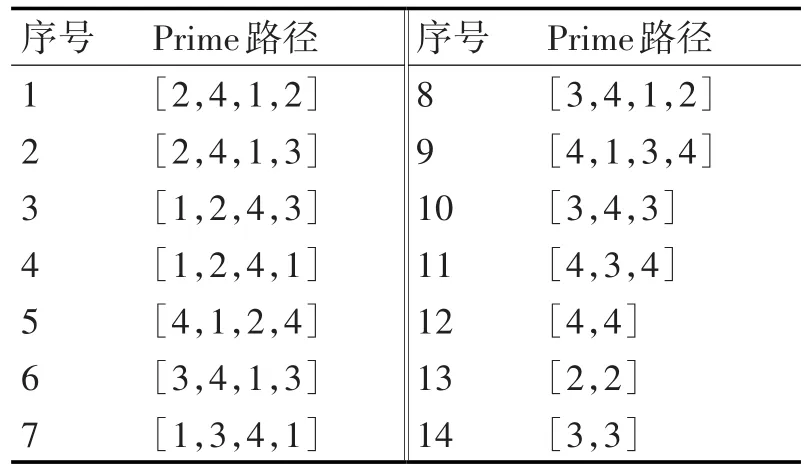
表1 Prime路径列表

如果图2采用基本路径覆盖，得到的基本路径集合如表2所示，虽基本路径集合是不唯一的，但基本路径集合的总数是确定的。由于基本路径也是测试路径，表2也给出了该基本路径覆盖Prime路径的情况，和每个基本路径生成对判定节点的取值影响情况。

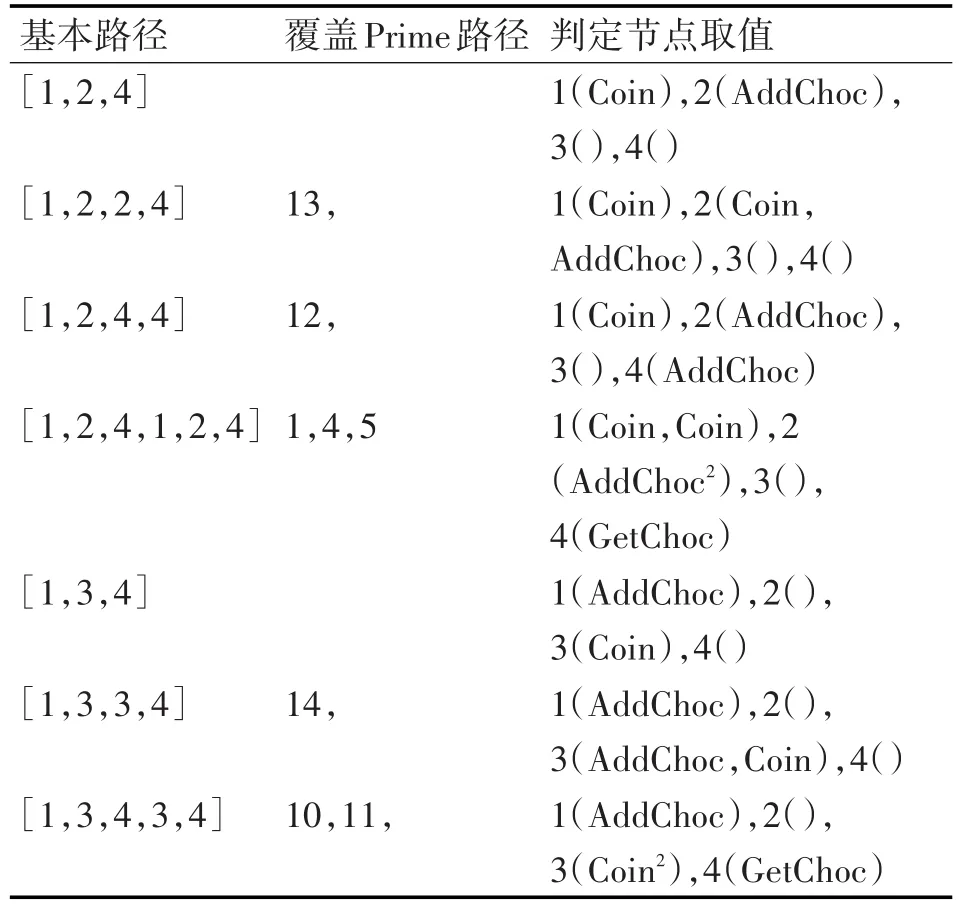
表2 基本路径及其覆盖信息列表

生成的基本路径并不能覆盖（3，4）和（4，1），（4，1）和（1，3）等的有效边对，因此，一些连续边对影响的行为无法检测出；而Prime路径能够覆盖最大可能的无环连续边对，但其产生的测试路径不唯一，表3中两组测试路径集合，虽然测试代价较小，但存在测试路径过长，实际测试时或因变迁和状态之间存在太多的约束，难以产生有效的测试数据驱动路径执行，且该测试路径并不能满足路径集合的独立性需求，制约系统行为检测能力。

采用InPrTestPath算法，图2产生的测试路径集合如表4所示。图2中有4个判定节点：节点1可取值AddChoc和Coin，节点2可取值AddChoc和Coin，节点3可取值可取值AddChoc和Coin，节点4可取值可取值AddChoc、和GetChoc。Anurag算法虽然总路径长度最短，但只有一条路径，即只有1个判定节点对路径生成起决定作用；Paul&Nan Li算法较Anurag算法而言，判定节点的独立性覆盖需求满足度有所提升，但也仅有2个判定对路径生成起决定作用。表4虽然路径数目、总路径长度都超过两类Prime路径生成算法，但该算法在生成每条新路径时只改变一个节点的判定值，4个判定节点均对路径生成起决定作用。通过分析新路径的判定节点满足度显而易见，表3中的两个Prime算法都无法满足判定节点的独立性覆盖需求，考虑兼顾独立性和连续边的覆盖分析，本文算法更易满足。

表3 最短总长度测试路径列表

5 结语

通过分析两种常见的面向路径覆盖的测试准则：Prime路径覆盖准和基本路径覆盖准则各自内涵及其优缺点，提出一种兼顾路径独立性和连续边覆盖的测试路径生成技术。生成算法采用面向两个目标的启发式选择策略，综合考虑测试路径总长度、判定节点独立性影响、测试路径数目、单测试路径长度等综合因素，通过本算法产生的测试路径集合即考虑路径独立性组合问题又考虑连续变迁覆盖问题，在保证覆盖充分性的同时，使得测试路径数和总测试路径长度在可测性前提下保持在合理的范围，从而保证测试覆盖度的前提下测试路径优化。

表4 一种覆盖独立性的Prime测试路径列表