滑翔制导炮弹自抗扰姿态解耦控制器设计

徐秋坪, 王旭刚, 王中原

(南京理工大学能源与动力工程学院, 江苏 南京 210094)

0 引 言

火箭助推滑翔增程制导炮弹具有低成本、高增程效率、远程精确打击以及高效毁伤等诸多优点,目前这类新型制导弹药已成为多国研究的热门课题[1-5]。该类制导炮弹由身管武器发射,出炮口后尾翼张开使弹丸达到某一设定转速并保持稳定飞行;几秒后弹上的小型火箭助推发动机工作以帮助弹丸爬升,发动机工作结束在升弧段某时刻弹载探测系统开始工作,在弹道顶点附近鸭舵张开,弹上制导控制系统调节舵机来不断调整炮弹的滑翔姿态,以实现增程和精确打击[6]。由于弹丸的旋转特性,控制指令与舵系统响应之间的延迟等因素会导致俯仰和偏航通道存在交叉耦合,并且会造成输出控制力存在一定的相位延迟。因此,解耦控制是滑翔制导炮弹控制系统设计必须要解决的问题。成本和发射平台的局限性使得为弹载传感器、处理器以及执行机构等诸多制导部件提供的可用空间是有限的,其提供的控制能力也是有限的[7],并且复杂的控制算法和控制器结构往往需要测量的状态信息较多,庞大的计算量会增加弹载计算机的负担,更多测量器件的引入会显著增加成本,同时还可能降低制导控制系统的可靠性,因此最大可能地简化控制系统组成并利用较少的测量信息和简易的控制算法达到较高品质的控制效果是制导炮弹未来的技术发展方向之一[8]。考虑在各种假设条件下建立的制导炮弹控制模型与实际飞行模型间存在差异,滑翔飞行中存在诸多不确定扰动,动力学参数的摄动,这些问题又对制导炮弹控制器的抗扰能力和鲁棒性提出了较高的要求。因此,设计不依赖于滑翔制导炮弹精确控制模型,并且对各通道间存在不确定性扰动、指令响应延迟和交叉耦合情况下仍具备高精度、强鲁棒性和适应性的解耦控制器显得尤为迫切。

对于上述滑翔制导炮弹控制系统设计问题(控制能力、传感器、系统复杂度等约束,抗扰、解耦、精度、鲁棒性等要求),本文将采用自抗扰控制技术(active disturbance rejection control, ADRC)[9-11]给予有效地解决。该技术的核心思想为:利用扩张状态观测器(extended state observer, ESO)实时跟踪估计由内扰和外扰构成的总和扰动,然后在控制律中对实时估计出的总和扰动进行补偿,使得原先含有未知扰动的不确定性的非线性系统转化为“积分串联器”型的线性对象[12]。ADRC在处理系统不确定性时不是让控制器根据对象而设计,而是让对象来适应控制器,并且它不依赖于对象精确的数学模型,能处理各种内外不确定性。通过大量的理论研究和实际工程应用表明,ADRC具有结构简单,易于实施,计算量小,控制精度高、品质好,鲁棒性强(恶劣环境下仍能保持良好的控制性能),可应用范围广等诸多优点,目前该技术已经在航空航天、伺服系统、工业过程控制等领域中获得了广泛的应用[13]。文献[14]运用自抗扰控制技术设计了飞行器的俯仰/偏航姿态控制器,但该方法中没有涉及为姿态跟踪指令安排过渡过程。文献[15]针对临近空间机动滑翔飞行器应用反步法和扩张状态观测器结合,提出了自抗扰反歩姿态控制器的结构,但控制参数较多、计算量大。文献[16]针对导弹拦截机动目标问题,将自抗扰控制的思想用于过载制导律的设计。文献[17]基于自抗扰控制和反演终端滑模控制,设计了一种导弹末制导控制一体化算法,以减小其脱靶量。文献[18]设计了飞行器俯仰、横侧(解耦)自抗扰姿态控制器。文献[19]针对微型飞行器参数不确定和扰动情况下采用ADRC设计了纵向控制算法。文献[20]以静不稳定运载飞行器为对象设计了线性自抗扰俯仰姿态控制器,并采用BP神经网络整定控制参数。文献[21]基于传统三回路结构,设计了导弹自抗扰三回路过载驾驶仪,但文章未考虑舵系统的延迟影响。但这些文献中未考虑交叉耦合的影响,也未涉及由于旋转引起的舵控量耦合。文献[22] 针对Have Dash II BTT导弹并考虑其气动参数摄动和外扰的情形,基于输入输出线性化来降阶模型并结合自抗扰控制技术,设计了三通道解耦的姿态控制器。

本文以滑翔制导炮弹为对象,考虑其控制模型中的不确定性,飞行中存在诸多不确定外部扰动,舵机响应指令的延迟,俯仰和偏航通道间存在交叉耦合等方面出发,基于自抗扰控制技术,设计适用于滑翔制导炮弹的非线性自抗扰姿态解耦控制器,解决存在交叉耦合、不确定内外扰动以及执行机构响应延迟情况下的抗扰和解耦控制问题。设计时引入虚拟控制量,并将各通道除去控制量以外的所有项视为该通道的总和扰动(包括交叉耦合动态和不确定项等),采用ESO对总和扰动进行实时估计,以实现交叉耦合通道的解耦;同时,对姿态指令信号安排合理的过渡过程,采用非线性状态误差反馈控制律使得系统的状态误差收敛于零,以实现输出姿态对给定指令的快速精确跟踪。通过数值仿真验证了该非线性自抗扰姿态解耦控制器的可行性和有效性。结果表明此控制器可在此类制导炮弹上有效地工作,计算量小且需调控制参数少,有利于减轻弹载计算机和控制系统的负担,易于工程实现。此外,该控制器还具有高控制精度,良好的抗干扰能力,对参数的摄动具备较强的适应性和鲁棒性等优势。

1 滑翔制导炮弹姿态耦合模型

假设滑翔制导炮弹在一小段无动力滑翔飞行过程中,飞行速度和弹体的转速基本不变,忽略动压、马赫数及各弹丸物理参数的变化,并且攻角和侧滑角均被视为小量,那么存在交叉耦合的滑翔制导炮弹运动模型可描述如下[23]:

(1)

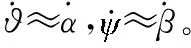
(2)

式中,k1=b3+a1,k2=b5+a2,k3=b1-b3a1+b5a2,k4=b2-b3a2-b5a1,k5=b4-b3a3,k6=b5a3,k7=a3。

显然,由模型(2)描述的姿态控制系统中两通道的姿态角和舵偏角均存在交叉耦合。

将舵机系统假设为二阶环节,为便于研究,此处仅考虑弹体旋转情况下俯仰和偏航等效舵偏角的稳态输出,即

(3)

其中

(4)

其详细推导过程可参考文献[24]。其中δzc,δyc分别为俯仰和偏航通道的等效舵偏角控制指令;ks为舵系统增益；Ts为舵系统时间常数；μs为舵系统阻尼比；τ为指令纯延迟时间；γd为总的延迟相位角。

(5)

式中

(6)

考虑模型因各种假设、忽略条件、近似处理等引起的未建模部分(内扰),记为ωin(t);以及飞行环境对模型的不确定外部扰动(外扰),记为ωout(t)。为便于分析,可将它们统一视为模型的不确定扰动ω(t),即ω(t)=ωin(t)+ωout(t)。

记u1=δyc,u2=δzc,x1=β,x2=α,那么由式(5)描述的模型可写成如下耦合控制系统:

(7)

基于ADRC设计制导炮弹姿态解耦控制器,选取合适的偏航/俯仰舵偏量u1(δyc),u2(δzc),使输出的侧滑角/攻角x1(β),x2(α)都能快速精确地跟踪上设定的姿态指令y1c(βc),y2c(αc)。

2 自抗扰姿态解耦控制器

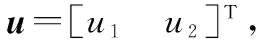
U=B0u

(8)

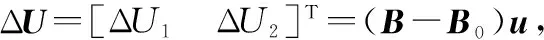
(9)

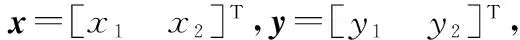
(10)

第i个通道的输入输出关系为

(11)

式中,Ui为其输入;yi为其输出。这样每一个通道的虚拟控制量Ui与输出yi之间变为单输入-单输出的关系,这意味着已完全实现了yi和Ui之间的解耦,相应的fi则是作用在该通道上的扰动总和。因此,只要测量出yi,那么在Ui和yi之间嵌入一个自抗扰控制器,即可完全能够让yi跟踪上yic。

对于上述存在不确定扰动的姿态耦合控制模型,本文设计的非线性自抗扰姿态解耦控制器主要由跟踪微分器(tracking differentiator, TD)、ESO和非线性状态误差反馈律(nonlinear state error feedback, NLSEF)三部分组成,其结构如图1所示。

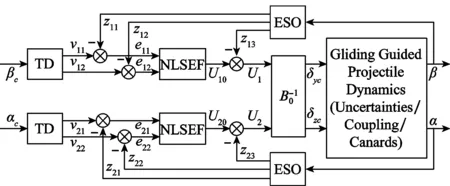
图1 滑翔制导炮弹自抗扰姿态解耦控制器结构Fig.1 ADRC based attitude decoupling controller diagram for gliding guided projectile

2.1 跟踪微分器

为避免初始舵偏控制量较大突变以致控制饱和,可通过TD对给定信号进行预处理,安排一个合适的过渡过程,让系统状态误差从零开始渐近变化,有利于实现对姿态指令的无超调、快速跟踪,并增强系统的稳定性。

本文利用如下离散形式的最速跟踪微分器[25]为第i个通道的输入指令yic安排过渡过程vi1,并提取其微分信号vi2：

(12)

式中,h为积分步长;h0为滤波因子,对噪声的抑制有着非常重要的作用。输入指令不需要滤波,则可选h0=h。r0为速度因子,用于调节输入信号的跟踪速度,它与过渡过程时间Td的关系为

(13)

式中,x0为给定输入值;x1为TD的初始值。

根据任务要求,只需选择合适的参数r0,使安排的过渡过程vi1能够最快地无超调地跟踪输入信号yic;当vi1充分地接近yic时,可将vi2当做yic的近似微分。

式(12)中函数fhan(x1,x2,r,h)的具体表达形式如下:

(14)

式中,sign(x)为符号函数。

2.2 扩张状态观测器

考虑式(10)描述的存在不确定扰动的耦合模型中的第i个通道,可写成如下形式:

(15)

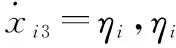
(16)

式中,非线性函数fal(e,λ,σ)的形式为

(17)

当0<λ2<λ1<1时,函数fal(e,λ,σ)具备“误差小时增益大和误差大时增益小”的变化特性,其中σ决定了它的线性区间宽度,适当增大σ可避免此函数在原点附近的振荡[13]。

此ESO的误差系统可表示为

(18)

当ESO进入稳态时,式(16)右端全收敛于零,则ESO的稳态误差为

(19)

由此可见,只要选取足够大于|ηi|的参数β03,则该ESO的稳态误差都会足够小,这意味着只要选择适当的参数,ESO的估计误差可在有限时间内达到足够小[13,26-27],那么zi1≈yi,zi2≈xi2,zi3≈fi。实际工程应用中常取λ1=0.5,λ2=0.25,σ=h。因此ESO设计参数只有β01,β02,β03,且可根据步长h初步调整出来:β01=1/h,β02=1/(1.6h1.5),β03=2/(52h2.2)。然后根据实际跟踪情况进行协调,主要调整β03的同时,适当调整β01和β02,不断改善估计效果。更多关于ESO参数选取可参考文献[10-11,13]。

2.3 非线性状态误差反馈律

由于设计的非线性ESO能够让其状态zi3实时准确地估计姿态控制系统的扰动总和fi,因此可利用zi3对原系统进行补偿。

若取第i个通道的Ui为

Ui=Ui0-zi3

(20)

则其对应的不确定系统(15)可变为如下二阶积分器串联型控制系统:

(21)

从而使不确定系统实现了动态补偿线性化。动态补偿线性化机制不依赖于系统精确的数学模型,利用扩张状态观测器即可将对象转化为简单的积分器串联型结构。

vi1是TD对第i个通道的输入yic安排的过渡过程,vi2是其微分信号,而zi1≈xi1,zi2≈xi2,则该通道的状态误差:ei1=vi1-zi1,ei2=vi2-zi2,则ei1,ei2决定的二阶积分器串联型对象为

(22)

取控制律

(23)

式中,r1>r>0,可使得闭环系统在有限时间内到达原点。证明如下:存在正定时间函数[13]

(24)

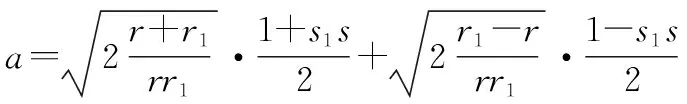
该正定时间函数沿系统轨线的导数为

(25)

因此,取上述反馈Ui0可使得闭环系统在有限时间内收敛到原点。

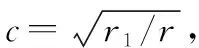
(26)

为避免进入稳态后的高频振荡,本文则采用系统(22)和反馈控制律(26)所对应的离散系统的快速最优控制综合函数[13,25]

Ui0=-fhan(ei1,cei2,r1,h1)

(27)

作为反馈控制律。由于篇幅所限,其离散系统快速最优控制综合函数fhan的具体推导过程可参考文献[13,25]。式中r1为控制量增益;c为阻尼因子,在误差反馈中起着阻尼作用;h1为精度因子,一般h1>4h。在跟踪阶跃指令时,为避免出现超调、振荡以及控制量的剧烈变化,可采用ei2=-zi2代替ei2=vi2-zi2,即将考虑vi2考虑为零。只要选取合适的参数(c、r1、h1),采用非线性状态误差反馈控制律(27),那么第i通道的状态误差微分系统可在有限时间内收敛于原点。因此,第i通道的输出攻角和侧滑角(yi)可在有限时间内跟踪上安排的过渡过程(vi1),又因为采用TD安排的过渡过程(vi1)可对输入信号(yic)实现有限时间无超调精确跟踪,故而实现了系统输出攻角和侧滑角(yi)对输入信号(yic)的快速精确跟踪。

通过对每个通道并行设计相同的自抗扰控制器,选择合适的虚拟控制量Ui,以保障各个通道的输出姿态角yi都能够快速且准确地跟踪上相应的姿态指令yic,既达到了抗扰效果,又实现了解耦控制。然后根据式(8)可计算出应用于耦合模型的实际控制量u,即

(28)

综上,本文设计的抗扰解耦控制器,将耦合控制系统中的模型不确定部分、耦合部分以及不确定外扰一并视为各个通道上的扰动总和(不需要各部分的具体精确模型),通过ESO被估计并给予补偿掉。B0对B的估计精度要求并不高,只要保证B0的可逆性,对闭环控制品质无多大影响。控制参数可以根据控制要求和步长大致整定出其初始值,然后再根据实际的跟踪效果和性能要求对它们进行微调(主调参数c和h1),直到达到所需的控制效果。

3 仿真分析

以某滑翔制导炮弹为例,考虑模型中存在不确定的内扰和外扰时,对设计的自抗扰姿态解耦控制器进行数值仿真,并对此方法的可行性和有效性进行评估。仿真采用零初始状态及欧拉数值方法求解,取步长h=1 ms。滑翔制导炮弹仿真参数如表1所示。

表1 滑翔制导炮弹参数

设定姿态角跟踪指令如下:

(29)

根据初始姿态角指令的幅值,设定过渡过程的时间为Td=0.25 s,那么由各阶段跟踪指令的最大偏差以及式(12)可确定出各阶段TD参数:

(30)

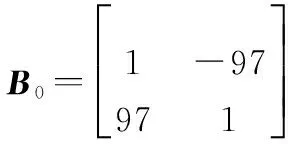
3.1 ωi(t)=0时的解耦跟踪效果

选择模型(9)中各通道的内外总扰动ωi(t)=0,即不考虑内扰和外扰,以考察本文设计的姿态控制器的解耦跟踪效果,并将其与文献[18,20]中基于ESO设计的PD解耦控制器(ESO-PD)进行对比分析,仿真结果如图2所示。结果表明,ESO-PD控制器对俯仰和偏航指令的跟踪存在超调现象,如图2(a)、图2(b)所示;并且从图2(e)、图2(f)可以看出其初始段两通道的等效舵偏角指令均较大,尤其当切换跟踪信号时其值会产生较大的突变,这不利于系统的稳定。而本文设计的ADRC姿态解耦控制器可实现对两通道姿态信号的快速、无超调、精确跟踪,解耦控制效果明显更好;并且两通道的等效舵偏角指令均由零开始缓慢地变化,有效地缓解了舵机的控制负担,当切换姿态角信号时不存在突变现象,利于系统的稳定控制。当输出姿态角跟踪上给定信号之后,等效舵偏角指令保持不变。从图2(e)～图2(h)可以看出,偏航通道等效舵偏指令比俯仰通道等效舵偏指令大很多,然而经舵机响应后的偏航通道等效舵偏角却比俯仰通道等效舵偏角小很多,这是与弹丸的飞行动态相符的。另外,图中fi与zi3的曲线几乎重合,说明ESO的状态变量能够实时精确地跟踪估计两通道的总和扰动。通过在控制舵偏指令中对估计的总和扰动补偿,使得输出攻角和侧滑角能够快速精确地跟踪上安排的过渡过程指令,进而跟踪上给定的姿态指令。因此,本文设计的结构简单、易于调参的自抗扰姿态解耦控制器体现出了较好的解耦控制品质,有利于系统的稳定,有效地解决了舵机响应延迟和交叉耦合带来的问题。

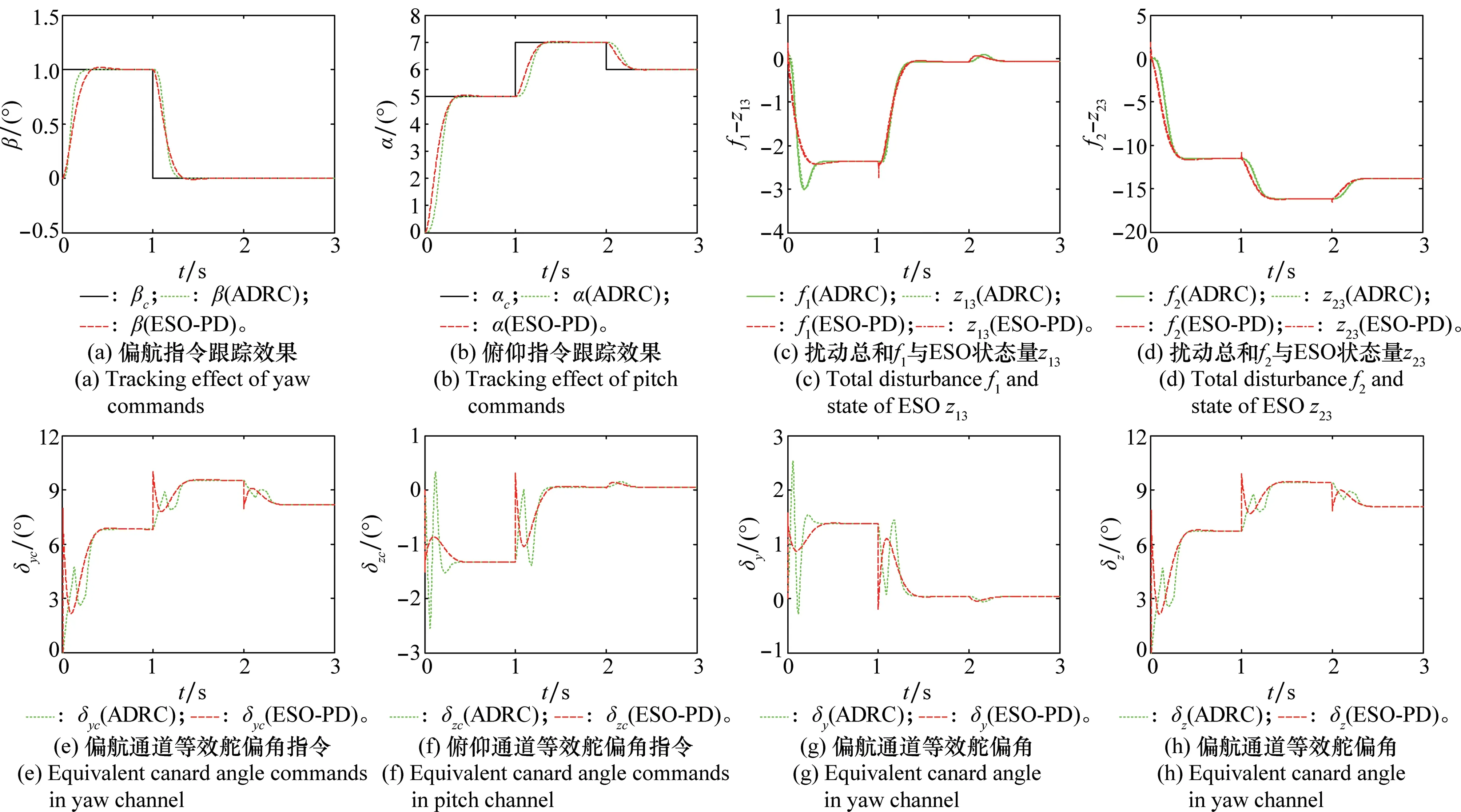
图2 ADRC控制器与ESO-PD控制器对比Fig.2 Comparison analysis between the proposed ADRC controller and ESO-PD controller

3.2 强扰动时的自抗扰解耦效果

考虑模型(9)中内外扰动的不确定性,本文选择连续正弦波扰动以及随机噪声的组合作为控制系统的内部扰动模型,并选择单位区间函数(在区间[a,b]上函数值为1,其余为0)作为外部扰动模型,具体形式如下:

(31)

式中,γ1,γ2,γ3分别为内扰、噪声以及外扰的强度;n0(t)为单位强度的随机高斯白噪声;[a,b]决定外扰扰作用的时间区间。分别选择俯仰和偏航通道未扰动时各个跟踪阶段的稳态|fi|的20%作为外扰强度,10%作为内扰强度,0.1%作为噪声强度,并假设外扰在第一个跟踪阶段作用区间为[0.6 s,0.7 s],第二阶段为[1.6 s,2 s],第三阶段无外扰。仿真结果如图3所示。在存在强扰动时,基于ESO的PD控制器则会受扰动的影响,存在较大超调和振荡现象,跟踪效果相对较差;并且初始等效舵偏角指令较大,当切换姿态信号时同样存在突变现象。而采用本文设计的自抗扰解耦控制器可使得俯仰/偏航通道输出攻角/侧滑角精确、快速、无超调地跟踪上设定的姿态指令,具备很好的抗扰能力。在高强度瞬时扰动和随机噪声扰动时,两通道ESO的状态均能实时准确有效地估计输出姿态角和扰动总和。俯仰和偏航通道的等效舵偏角指令均从零开始缓慢变化,且当切换跟踪信号时其值不存在较大的突变,再次验证了本文设计的控制器更有利于系统稳定和减轻执行机构控制负担的优势。当扰动小时,舵偏指令变化小且变化率也小,大扰动时则需要较大的舵偏来补偿扰动,但是两通道舵偏指令的变化均能够满足舵系统约束,并且经舵系统响应后,俯仰和偏航通道的等效舵偏角规律均符合系统动态。

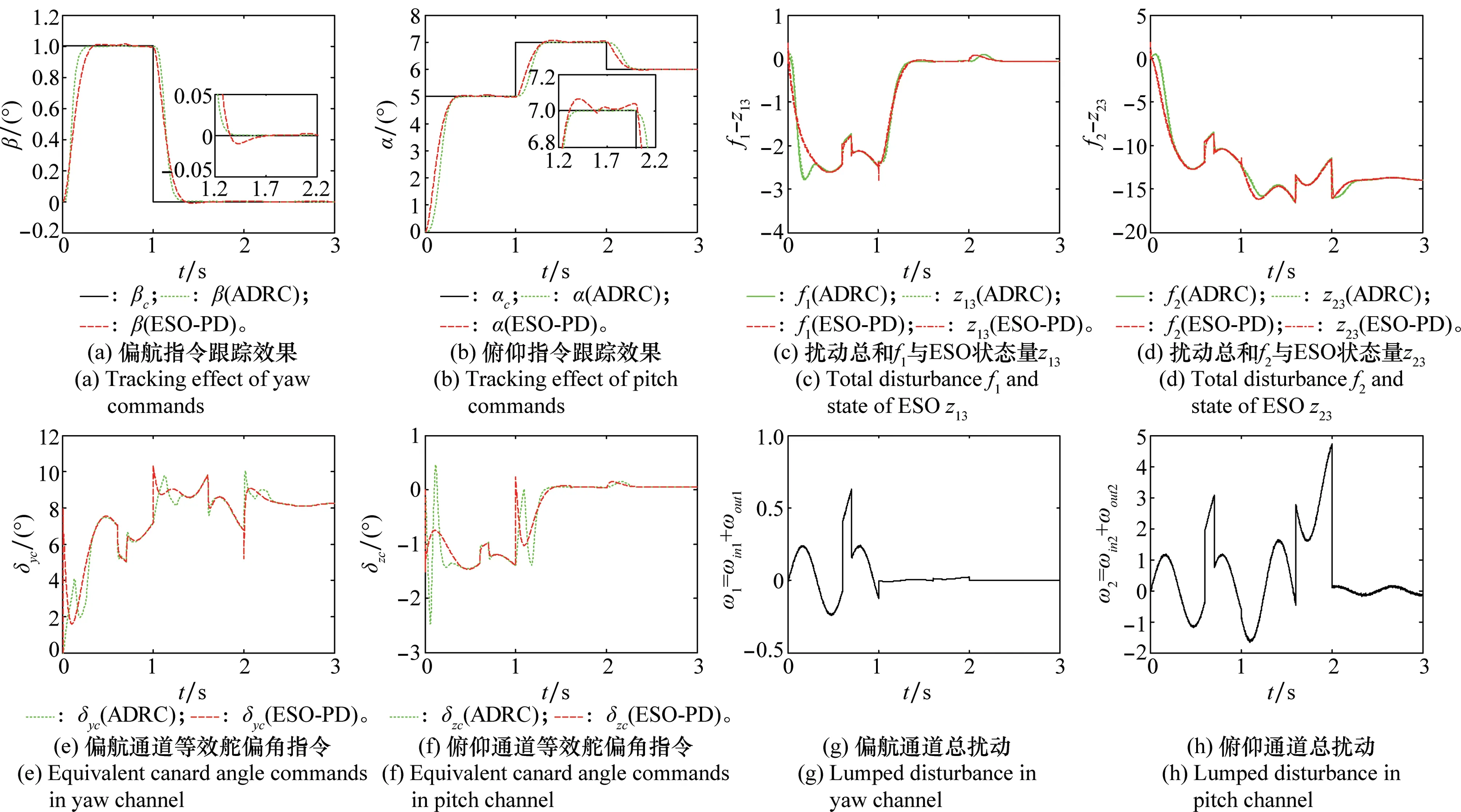
图3 强扰动下的自抗扰解耦效果Fig.3 Active disturbance rejection and decoupling effect with strong disturbances

3.3 参数摄动时自抗扰解耦控制器的鲁棒性

上述仿真表明自抗扰姿态解耦控制器在强内外扰动时可直接实现无静差解耦控制,达到了很好的跟踪效果,并且具备较强的抗扰能力。为考察系统的鲁棒性和适应性,对动力学系数摄动25%,并代入到100次独立的仿真试验中,计算结果如图4所示。如果考虑第3.2节提及的强内、外扰动模型的影响,其仿真结果如图5所示。可以看出,不管是否存在强内外扰动,一旦设计的姿态解耦控制器的控制参数被调整好后,那么它们对于一定范围内的模型参数的摄动是不敏感的,此解耦控制器仍能够实现对给定姿态指令的精确、稳定跟踪,具有较强的干扰抑制能力、鲁棒性和适应性,同时也进一步充分验证了利用ADRC设计姿态控制器时不依赖其系统精确模型的优势。

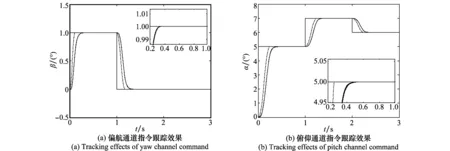
图4 参数摄动时控制器的鲁棒性分析Fig.4 Robustness analysis of the proposed controller with perturbed aerodynamic parameters

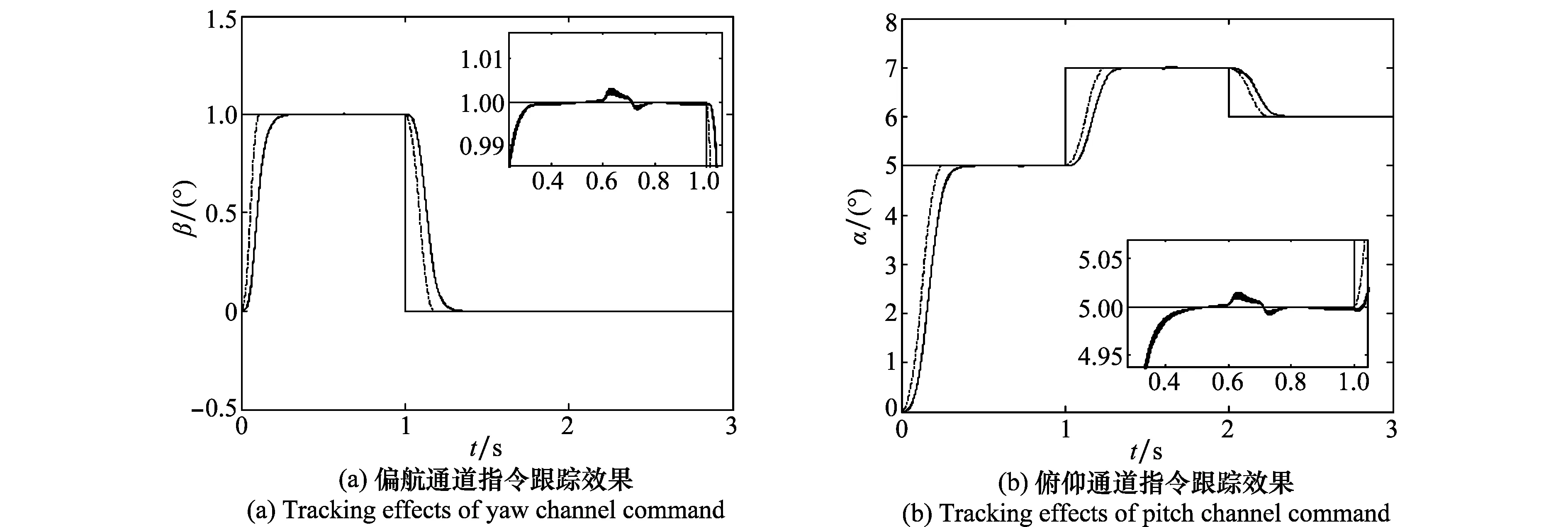
图5 强扰动下参数摄动时控制器的鲁棒性分析Fig.5 Robustness analysis of the proposed controller with perturbed aerodynamic parameters and strong disturbances

4 结 论

本文针对滑翔制导炮弹控制系统设计时面临的不确定性扰动和解耦控制问题(包括模型未建模部分、飞行环境对模型的外部扰动、舵机响应的延迟以及交叉耦合等因素),设计了控制回路简单、计算量小、需调控制参数少,易于工程实现的自抗扰姿态解耦控制器。

该控制器的可行性和有效性通过数值仿真得以验证。结果表明设计的自抗扰姿态解耦控制器可有效地应用于此类制导炮弹,能够实现俯仰/偏航解耦控制,并快速精确地跟踪上姿态指令。两通道的等效舵偏角指令均从零开始缓慢变化,有效地减轻了执行机构的控制负担。控制参数对较大范围内的模型参数摄动不敏感,具备较强的抗干扰能力、适应性和鲁棒性,为该类制导炮弹的控制系统设计提供一定的工程应用参考。

[1] COSTLLO M F. Range extension and accuracy improvement of an advanced projectile using canard control[C]∥Proc.of the AIAA Atmospheric Flight Mechanics Conference, 1995: 324-331.

[2] COSTLLO M F. Extended range of a gun launched smart projectile using controllable canards[J].Shock and Vibration,2001,8(3): 203-213.

[3] WANG Z Y. Analysis of gliding control for an extended-range projectile[C]∥Proc.of the 22th International Symposium on Ballistics, 2005: 46-53.

[4] WANG Z Y, ZHOU W P, CHEN S S. The design and experimental tests of aerodynamic shapes for an extended-range projectile[C]∥Proc.of the 23th International Symposium on Ballistics, 2007: 731-738.

[5] ELSAADANY A, YI W J. Extended range of fin stabilized projectile using movable canards[J]. Information Technology Journal, 2014, 13(17): 2658-2665.

[6] 史金光, 王中原, 曹小兵, 等. 滑翔增程弹箭滑控段弹体运动模式对增程效率的影响[J]. 兵工学报, 2007, 28(6): 651-655.

SHI J G, WANG Z Y, CAO X B, et al. Effect of motorial modes of gliding extended range projectile on range extended efficiency[J]. Acta Armamentarii, 2007, 28(6): 651-655.

[7] FRESCONI F. Guidance and control of a projectile with reduced sensor and actuator requirements[J]. Journal of Guidance, Control, and Dynamics, 2011, 34(6): 1757-1766.

[8] 杨树兴, 赵良玉, 闫晓勇. 旋转弹动态稳定性理论[M]. 北京:国防工业出版社, 2014: 133-160.

YANG S X, ZHAO L Y, YAN X Y. Dynamic stability of spinning missiles[M]. Beijing: National Defense Industry Press, 2014: 133-160.

[9] 韩京清.自抗扰控制器及其应用[J].控制与决策, 1998, 13(1): 19-23.

HAN J Q. Auto disturbances rejection controller and its applications[J]. Control and Decision, 1998, 13(1): 19-23.

[10] 韩京清. 自抗扰控制技术[J]. 前沿科学, 2007 (1): 24-31.

HAN J Q. Auto disturbances rejection control technique[J]. Frontier Science, 2007(1): 24-31.

[11] HAN J Q. From PID to active disturbance rejection control[J]. IEEE Trans.on Industrial Electronics, 2009, 56(3): 900-906.

[12] ZHENG Q, GAO Z Q. Active disturbance rejection control: between the formulation in time and the understanding in frequency[J].Control Theory and Technology,2016,14(3):250-259.

[13] 韩京清.自抗扰控制技术——估计补偿不确定因素的控制技术[M].北京:国防工业出版社, 2013.

HAN J Q. Active disturbance rejection control technique-the technique for estimating and compensating the uncertainties[M]. Beijing: National Defense Industry Press, 2013.

[14] HUANG Y, XU K K, HAN J Q, et al. Flight control design using extended state observer and non-smooth feedback[C]∥Proc.of the 40th IEEE Conference on Decision and Control, 2001: 223-228.

[15] 李菁菁, 任章, 曲鑫. 机动滑翔飞行器的自抗扰反步高精度姿态控制[J]. 系统工程与电子技术, 2010, 32(8): 1711-1715.

LI J J, REN Z, QU X. Design of active disturbance rejection back stepping attitude controller for maneuvering glide vehicles[J]. Systems Engineering and Electronics,2010,32(8):1711-1715.

[16] ZHAO C Z, HUANG Y. ADRC based integrated guidance and control scheme for the interception of maneuvering targets with desired LOS angle[C]∥Proc.of the 29th Chinese Control Conference, 2010: 6192-6196.

[17] 董朝阳, 程昊宇, 王青. 基于自抗扰的反步滑模制导控制一体化设计[J]. 系统工程与电子技术, 2015, 37(7): 1604-1610.

DONG C Y, CHENG H Y, WANG Q. Backstepping sliding mode control for integrated guidance and control design based on active disturbance rejection[J]. Systems Engineering and Electronics, 2015, 37(7): 1604-1610.

[18] 杨瑞光, 孙明玮, 陈增强. 飞行器自抗扰姿态控制优化与仿真研究[J]. 系统仿真学报, 2010, 22(11): 2689-2693.

YANG R G, SUN M W, CHEN Z Q. ADRC-based attitude control optimization and simulation[J]. Journal of System Simulation, 2010, 22(11): 2689-2693.

[19] BALAJIWALE S, ARYA H, JOSHI A. Study of performance of ADRC for longitudinal control of MAV[J]. IFAC-Papers OnLine, 2016, 49(1): 585-590.

[20] 吴其霞,马顺健,孙明玮,等.静不稳定运载飞行器自抗扰姿态控制的参数整定研究[J].战术导弹技术,2016(2): 63-69.

WU Q X, MA S J, SUN M W, et al. Research on tuning of active disturbance rejection attitude controller for statically unstable launch vehicle[J].Tactical Missile Technology,2016(2):63-69.

[21] 孙明玮,徐琦,陈增强,等.自抗扰三回路过载驾驶仪的设计[J].北京理工大学学报,2015,35(6):592-596.

SUN M W, XU Q, CHEN Z Q, et al. Active disturbance rejection three-loop acceleration autopilot design[J]. Transactions of Beijing Institute of Technology, 2015, 35(6): 592-596.

[22] 张保群, 宋申民, 陈兴林. 基于自抗扰控制的BTT飞行器自动驾驶仪设计[J]. 航天控制, 2010, 28(1): 46-52.

ZHANG B Q, SONG S M, CHEN X L. Bank-to-turn missile autopilot design based on active disturbance rejection control[J]. Aerospace Control, 2010, 28(1): 46-52.

[23] 钱杏芳, 林瑞雄, 赵亚男. 导弹飞行力学[M]. 北京:北京理工大学出版社, 2008: 90-111.

QIAN X F, LIN R X, ZHAO Y N. Missile flight dynamics[M]. Beijing: Beijing Institute of Technology Press, 2008: 90-111.

[24] YAN X Y, YANG S X, ZHANG C. Coning motion of spinning missiles induced by the rate loop[J]. Journal of Guidance, Control, and Dynamics, 2010, 33(5): 1490-1499.

[25] 韩京清, 袁露林. 跟踪—微分器的离散形式[J].系统科学与数学, 1999, 19(3): 268-273.

HAN J Q, YUAN L L. Discrete-time form of tracking differentiator[J]. Systems Science and Complexity, 1999, 19(3): 268-273.

[26] HUANG Y, HAN J Q. Analysis and design for the second order nonlinear continuous extended states observer[J]. Chinese Science Bulletin, 2000, 45(21): 1938-1944.

[27] LI J, XIA Y Q, QI X, et al. On the necessity, scheme, and basis of the linear-nonlinear switching in active disturbance rejection control[J]. IEEE Trans.on Industrial Electronics, 2017, 64(2): 1425-1435.