基于PEV准则的I-UMOP问题求解方法
孟祥飞, 王 瑛, 亓 尧, 吕茂隆, 李 超
(空军工程大学装备管理与安全工程学院, 陕西 西安 710051)
0 引 言
经典的多目标规划问题(multi-objective programming, MOP)是最优化理论的一个重要分支,在管理学、军事学等领域具有广泛的应用,并且取得了许多重要成果[1-3]。经典多目标规划其主要解决的是确定环境下的决策问题。然而,在实际面临的决策问题中,往往存在大量的不确定因素。例如,在进行电厂发电调度[4]或飞行流量优化时,需要考虑种种不确定因素,在此基础上建立的调度模型是一个不确定多目标规划模型。如何求解这类不确定多目标规划问题具有重要的现实意义。
为解决该问题,学者们分别从不同角度刻画这种不确定因素。一部分学者将这类不确定性因素看作是随机因素,认为是随机造成了不确定,于是针对概率论和统计学的研究蓬勃发展起来[5-6]。然而,其他学者认为随机并不是造成不确定现象的唯一原因,现实世界中还存在一类不同于随机性的不确定现象,即专家信度[7-9]。为解决这种带有专家信度的多目标规划问题,许多学者基于模糊集理论[10]和可能性测度[11],将其转化为模糊多目标规划问题进行研究,文献[12]针对结构力学问题提出了基于测量数据的模糊分析方法。然而,当使用模糊变量描述专家信度时,可能会做出错误的决策[13-14]。为了更好地刻画专家信度,文献[15-17]建立了不确定理论,经过十多年的发展,已经形成了一个较为成熟的数学系统。因此,在处理带有专家信度的实际多目标规划问题时,可通过建立不确定多目标规划(uncertain multi-objective programming problem,UMOP)模型再进行求解。通常情况下所建模型中目标函数之间是相互独立的不确定多目标规划(independent-uncertain multi-objective programming problem,I-UMOP)模型。
传统求解方法往往是先将UMOP问题通过期望准则转化为确定的MOP问题再进行求解,但在转化过程中可能忽略了原问题的不确定性本质而且仅用期望准则难以反映不确定变量的波动性。鉴于此,本文首先通过不确定变量之间的序关系定义UMOP问题的有效解,然后基于序关系将其转化为不确定单目标规划问题,再进一步引入期望-方差准则将原问题转化为确定的单目标规划问题进行求解,最后证明求解得到的最优解是原UMOP问题的有效解。
1 求解方法基本框架
I-UMOP是指各个目标函数独立的不确定多目标规划问题,其模型为
(1)
式中,x∈Rn为决策变量;ξ1,ξ2,…,ξp为定义在不确定空间(Γ,L,M)上的不确定变量且相互独立;η1,η2,…,ηm为定义在不确定空间(Γ,L,M)上的不确定变量且相互独立。
期望-方差准则(PEV准则)[10]ξ和η是相互独立的不确定变量,ξp=(p)η当且仅当E[ξ]≤(<)E[η]且V[ξ]≤(<)V[η]。其中,E[·]和V[·]分别表示不确定变量的期望与方差。

其中至少存在一个j0,1≤j0≤p,使得
求解UMOP问题首先是利用某种方法(构造实值可测函数F)将其转化为不确定单目标问题,其表达式为
(2)
文献[10]已经证明U(x,ξ)是一个不确定变量。在PEV准则下,将问题(2)转化为确定的单目标规划问题,其表达式为
(3)
问题(3)的最优解便是问题(1)的Pareto有效解。
2 相关引理证明
为证明问题(3)的最优解是问题(1)的Pareto有效解,在PEV准则下提出以下引理。
引理1ξ和η是分别服从正则不确定分布Φ和Ψ且相互独立的不确定变量。若ξp=(p)η,则对于任意正实数λ,λξp=(p)λη成立。
证明由于ξp=(p)η,根据PEV准则,可得
E[ξ]≤(<)E[η]
(4)
V[ξ]≤(<)V[η]
(5)
根据不确定变量期望和方差计算公式,由式(4)、式(5),得

(6)

(7)
对于任意正实数λ,有

(8)

(9)
即

(10)

(11)
根据不确定变量的期望和方差的运算法则,有
E(λξ)≤(<)E(λη)
(12)
V(λξ)≤(<)V(λη)
(13)
即λξp=(p)λη成立。
证毕
引理2ξ1,ξ2是分别服从正则不确定分布Φ1,Φ2且相互独立的不确定变量,η1,η2是分别服从正则不确定分布Ψ1,Ψ2且相互独立的不确定变量。若ξ1p=η1,ξ2pη2或ξ1pη1,ξ2p =η2,则ξ1+ξ2pη1+η2成立。
证明不失一般性,以ξ1p=η1,ξ2pη2为例,根据PEV准则,可得
E(ξ1)≤E(η1)
(14)
V(ξ1)≤V(η1)
(15)
E(ξ2) (16) V(ξ2) (17) 根据不确定变量的期望和方差计算公式,由式(14)~式(17),可得 (18) (19) (20) (21) 式(18)与式(20)相加,可得 (22) 式(19)与式(21)相加,可得 (23) 根据不确定变量的期望运算法则,有 E[ξ1+ξ2] (24) 因ξ1,ξ2相互独立,有 eξ1eξ2-eξ1eξ2-eξ2eξ1+eξ1eξ2=0 (25) 同理 (26) 根据式(23)、式(25)及式(26),有 (27) 即 (28) (29) V[ξ1+ξ2] (30) 即ξ1+ξ2pη1+η2成立。 证毕 引理3ξ,η是分别服从正则不确定分布Φ和Ψ且相互独立的不确定变量,且两者下界ξ0,η0存在,记t0=min(ξ0,η0),若ξp=(p)η,则(ξ-t0)2p=(p)(η-t0)2成立。 证明由于ξp=(p)η,根据PEV准则,可得 E[ξ]≤(<)E[η] (31) 即 (32) 因为ξ0,η0分别是不确定变量ξ,η的下界,即分别是Φ-1(α)和Ψ-1(α)的下界,于是 Φ-1(α)-t0≥0,Ψ-1(α)-t0≥0 根据式(32),可得 (33) 由于(ξ-t0)2和(η-t0)2分别关于ξ和η单调递增,因此其逆分布分别为(Φ-1(α)-t0)2和(Ψ-1(α)-t0)2,根据期望计算公式,有 (34) (35) 故 E[(ξ-t0)2]≤(<)E[(η-t0)2] (36) 根据运算法则,有 V[(ξ-t0)2]=E{[(ξ-t0)2-E[(ξ-t0)2]]2}= E{(ξ-t0)4-2E[(ξ-t0)2](ξ-t0)2+E2[(ξ-t0)2]}= E[(ξ-t0)4]-2E2[(ξ-t0)2]+E2[(ξ-t0)2]= E[(ξ-t0)4]-E2[(ξ-t0)2] (37) 由式(37)可得 V[(η-t0)2]-V[(ξ-t0)2]= E[(η-t0)4-(ξ-t0)4]- (E[(η-t0)2]+E[(ξ-t0)2]) (E[(η-t0)2]-E[(ξ-t0)2]) (38) 根据式(38),有 E{[(η-t0)2+(ξ-t0)2][(η-t0)2-(ξ-t0)2]}- E[(η-t0)2+(ξ-t0)2]E[(η-t0)2-(ξ-t0)2]= [(Ψ-1(α)-t0)2-(Φ-1(1-α)-t0)2]}dα- (39) 令 f(α)=(Ψ-1(α)-t0)2+(Φ-1(α)-t0)2, h(α)=(Ψ-1(α)-t0)2-(Φ-1(1-α)-t0)2 两者均为关于α的增函数,则原式化为 V[(η-t0)2]-V[(ξ-t0)2]= (40) 引进辅助函数 (41) 对式(41)求导,可得 (42) 又G(0)=0,故G(1)≥0,即 V[(η-t0)2]-V[(ξ-t0)2]≥0 (43) 根据式(36)和式(43),有(ξ-t0)2p=(p)(η-t0)2成立。 证毕 证明由于ξp=(p)η,根据PEV准则,可得 E[ξ]≤(<)E[η] (44) 根据不确定变量的期望的计算公式,可得 (45) (46) 即 (47) 又 (48) 根据引理3关于方差部分的推导过程,有 (49) 证毕 将UMOP问题如式(1)转化为不确定单目标规划问题如式(2)的过程,通常采用线性加权法或理想点法。分别就两种方法证明其解的有效性。 线性加权法是通过对每个目标函数赋予相应的权值并线性加权求和将问题(1)转换得到的等价的问题模型为 (50) 定理1问题(50)在PEV准则下求解的最优解是问题(1)的PEV—Pareto有效解。 且存在至少一个i0,1≤i0≤p,使得 (51) (52) 即 (53) 于是 (54) 由定义1可知,x*不是问题(50)的最优解。这与假设矛盾,因此假设不成立,即x*是问题(1)在PEV准则下的Pareto有效解。 证毕 理想点法是通过最小化各目标函数与理想点之间的距离之和将问题(1)转化为等价的问题模型为 (55) 定理2问题(55)在PEV准则下求解的最优解是问题(1)的PEV—Pareto有效解。 且存在至少一个i0,1≤i0≤p,使得 (56) (57) 即 (58) 当i≠i0时,有 (59) 根据引理2,有 (60) (61) 即 (62) 根据引理4,有 (63) (64) 即 (65) 于是 (66) 由定义1可知,x*不是问题(55)的最优解。这与假设矛盾,因此假设不成立,即x*是问题(1)在PEV准则下的Pareto有效解。 证毕 为验证求解方法的可行性和有效性,设计了一个不确定多目标规划问题如式(67),问题中各目标函数较复杂且约束条件不规则。其中x1,x2是连续的非负决策变量,ξ1,ξ2,ξ3,ξ4,ξ5,ξ6是相互独立的不确定变量且分别服从不确定分布L(1,3),L(2,4),L(3,5),L(4,6),L(5,7),L(6,8);η1,η2是相互独立的不确定变量且分别服从不确定分布Z(1,2,3),Z(2,3,4)。 (67) 利用线性加权法将不确定多目标规划转换成不确定单目标规划,不妨令λ1=0.3,λ2=0.3,λ3=0.4,当权重变化时,可依然按此法求解。转换结果如下: 不确定单目标规划转换成确定的单目标规划,结果为 各不确定变量的分布及其逆分布见表1。 表1 各不确定变量的分布及其逆分布 模型进一步转化为 其中 (2α-5)(x1+0.5)(cos(2x2)+1)+ (2α-6)(x2+0.5)(sin(2x1)+1)+35 (2α-8)(sin(2x1x2)+1) 考虑转化后的目标函数仍非常复杂且局部极小点较多,因此采用文献[18]中的GA-PSO算法进行求解。该算法的具体流程见图1。GA算法以概率的方式进行选择、交叉、变异算子操作,增强了PSO算法的全局寻优能力,提高了收敛速度。参数设置见表2。 图1 GA-PSO算法流程图Fig.1 Sketch map of GA-PSO algorithm 算法参数取值交叉概率pc0.6变异概率pm0.1学习因子c11.495学习因子c21.495进化次数maxgen1000种群规模popsize30粒子更新速度Vmax1粒子更新速度Vmin-1 解得x1=0.538 9,x2=2.599 4函数目标值为3.479 3。其收敛速度见图2。从图2中可以看出,大约在第850代时,迭代收敛。 图2 线性加权模型求解收敛曲线Fig.2 Convergence curve of linear weighted method 线性加权法中各个目标函数的权重反映了决策者对各目标函数的偏重程度。当各权重发生变化时,期望和方差均会变化,导致转化得到的单目标函数会变化,从而对结果产生一定的影响。当目标函数的权重发生变化时,可按照算例1中的步骤计算。 采用理想点法求解时,根据各目标函数关于其相关不确定变量的单调性,在可行域内分别计算出3个目标函数的下界:1.336 1,-4.738 7,-10.357 6,采用GA-PSO算法求解计算结果为x1=0.536 5,x2=2.562 7,目标函数值为2.938 6。收敛效果见图3。从图3中可以明显看出,大约在第900代时,迭代收敛。 图3 理想点模型求解收敛曲线Fig.3 Convergence curve of ideal point method 传统求解方法是先将不确定多目标规划问题通过期望准则转化为确定的多目标规划问题再进行求解。采用理想点法求解,计算3个确定目标函数的最小值,结果分别为2.297 3,2.580 9,-7.994 4.采用GA-PSO算法进行求解,并与本文提出的方法对比,见表3。 表3 两种求解方法结果比较 如表3所示,传统方法与本文的方法在求解I-UMOP问题时结果不太相同。其主要原因在于:一是本文提出的方法在求解时首先计算每个不确定目标的函数的最小值,在一定程度上保持了原问题的不确定性本质,传统方法则首先计算转化后确定的目标函数的最小值,更加注重原问题的多目标本质,而没有考虑其不确定的本质;二是本文的方法是在期望-方差准则下求解,考虑了不确定变量的波动性,而传统方法是在期望准则下求解,没有考虑不确定变量的波动性。因此,虽然两种方法都可以对I-UMOP问题进行求解,且运算量相差不大,但是本文的方法更加注重保持问题的不确定本质和不确定变量的波动性。 (68) 采用理想点法将问题(68)转化为单目标问题,并利用文献[19]的二进制狼群算法进行求解,其算法流程见文献[19],参数设置见表4。 表4 二进制狼群算法参数设置 分别对3个目标函数进行优化求解,得到各目标价值的最优解如表5所示。 表5 各个目标价值的单目标最优解上限值 表5中,最优解向量分别为 采用二进制狼群算法求解,其收敛效果如图4所示。从图4中可以看出,算法在第162代左右收敛,并且收敛于0.895,求解得到最优解为IB。 图4 二进制狼群算法求解不确定背包问题收敛图Fig.4 Convergence of uncertain knapsack problem solving by binary wolf pack algorithm 具体求解结果见表6,表中给出了各个目标函数的最优解、本文方法计算得到的最优解和传统方法计算得到的最优解。经过对比,本文方法计算的最优解综合考虑了各个单目标价值的理想属性,并且在保持原问题不确定性本质的基础上计算得到该算例的帕累托最优解。 表6 不确定多目标背包算例优化求解结果 传统求解UMOP问题有以下两点不足:其一,传统方法容易忽略原问题的不确定性,而且当各个目标之间含有相同的不确定变量时,这种方法割裂了各个不确定目标之间的相关性;其二,传统方法仅用期望值作为转化准则难以反映原目标函数作为一个不确定变量的波动性。鉴于此,本文首先通过引入不确定变量之间的序关系定义了I-UMOP问题的有效解,然后基于序关系将其转化为不确定单目标规划解决第一个问题,进一步通过引入期望-方差准则将原问题转化为确定的单目标规划解决了第二个问题,并证明了求解得到的最优解解是原问题的有效解。最后,设计了两类数值算例,并分别利用GA-PSO算法和二进制狼群算法进行求解,结果表明本文提出的求解方法是可行且有效的。 [1] MIETTINEN K. Nonlinear multiobjective optimization[M]. Dordrecht: Kluwer Academic Press, 1998. [2] PADHAN S K, NAHAK C. Higher-order symmetric duality in multiobjective programming problems under higher-order invexity[J].Applied Mathematics and Computation, 2011,218(5): 1705-1712. [3] LAI H C, HO S C. Optimality and duality for nonsmooth multiobjective fractional programming problems involving exponential VV-rr-invexity[J]. Nonlinear Analysis, 2012, 75(6): 3157-3166. [4] KOU Y N, ZHENG J H, LI Z G. Many-objective optimization for coordinated operation of integrated electricity and gas network[J]. Journal of Modern Power Systems and Clean Energy, 2017, 5(3): 350-363. [5] PAVAN K Y V, BHIMASINGU R. Renewable energy based microgrid system sizing and energy management for green buil-dings[J]. Journal of Modern Power Systems and Clean Energy, 2015, 3(1): 1-13. [6] STANCU-MINASIAN I M. Stochastic programming with multiple objective functions[J]. Mathematical Reports, 1984, 27(1): 49-67. [7] WANG Z T, GUO J S, ZHENG M F, et al. A new approach for uncertain multi-objective programming problem based on PE principle[J]. Journal of Industrial and Management Optimization, 2015, 11(1): 13-26. [8] XIE G H, ZHANG J S, LIU R G. Application of matrix-based system reliability method in complex slopes[J]. Journal of Central South University, 2013, 20(3): 812-820. [9] LIU B D. Why is there a need for uncertainty theory[J]. Journal of Uncertain Systems, 2012, 6(1): 3-10. [10] 王族统.基于不确定理论的多目标规划方法及其应用研究[D]. 西安: 空军工程大学, 2015. WANG Z T. Research on multi-objective programming and apply based on uncertainty theory[D]. Xi’an: Air Force Engineering University, 2015. [11] LIU B D. Uncertainty distribution and independence of uncertain processes[J]. Fuzzy Optimization and Decision Making, 2014, 8(1): 3-12. [12] ZHAO J S, QIU X Y, MA J M, et al. Multi-objective optimization method of microgrid based on fuzzy clustering analysis and model recognition[J].Power System Technology, 2016, 40(8): 2316-2323. [13] ZADEH L A. Fuzzy sets as a basis for a theory of possibility[J]. Fuzzy Sets and Systems, 1978, 1(1): 3-28. [14] 王晓军, 杨海峰, 邱志平, 等. 基于测量数据的不确定性结构分析的模糊理论[J]. 北京航空航天大学学报, 2010, 36(8): 887-891. WANG X J, YANG H F, QIU Z P, et al. Fuzzy theory for uncertain structural analysis based on measurement data[J]. Journal of Beijing University of Aeronautics and Astronautics, 2010, 36(8): 887-891. [15] WANG Z T, GUO J S, ZHENG M F, et al. Uncertain multi-objective travelling salesman problem[J]. European Journal of Operational Research, 2015, 241(2): 478-479. [16] LIU B D, YAO K. Uncertain multilevel programming: algorithm and applications[J]. Computers & Industrial Engineering, 2015, 89: 235-240. [17] LIU B D. Uncertainty theory[M]. 5th ed. Berlin: Springer-Verlag, 2016. [18] 刘琼,刘炜琪,张超勇.基于GA-PSO的多目标混流装配线排序问题[J].华中科技大学学报(自然科学版),2011,39(10):1-5. LIU Q, LIU W Q, ZHANG C Y. Hybrid GA-PSO algorithm for sequencing multi objective mixed-model assembly lines[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2011, 39(10):1-5. [19] 吴虎胜, 张凤鸣, 战仁军, 等. 利用改进的二进制狼群算法求解多维背包问题[J]. 系统工程与电子技术, 2015, 37(5): 1084-1091. WU H S, ZHANG F M, ZHAN R J, et al. Improved binary wolf pack algorithm for solving multidimensional knapsack problem[J].System Engineering and Electronics,2015,37(5):1084-1091.


















3 有效解证明
3.1 线性加权法



3.2 理想点法
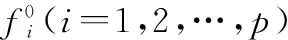


4 数值算例
4.1 算例1






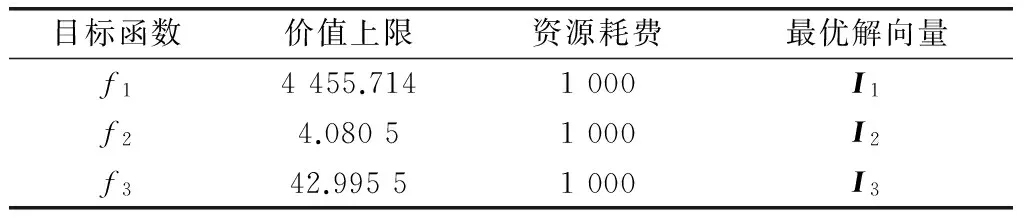
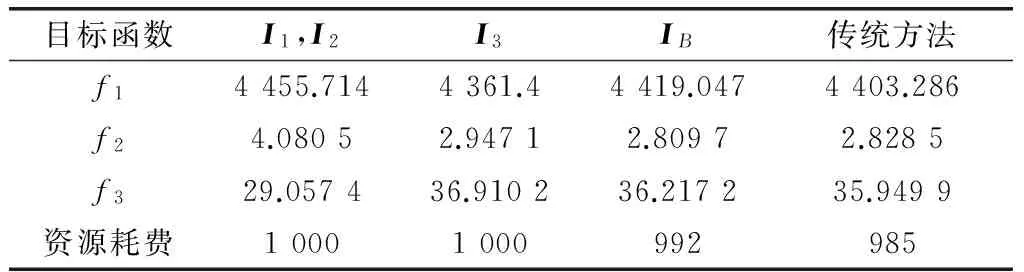
4.2 算例2
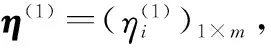



5 结 论

