基于奇异值熵和分形维数的雷达信号识别

曲志昱, 毛校洁, 侯长波

(哈尔滨工程大学信息与通信工程学院, 黑龙江 哈尔滨 150001)

0 引 言

随着数字技术的飞速发展,雷达信号的调制方式越来越复杂,对雷达信号调制方式识别是电子战系统的关键技术之一。对于雷达对抗和电子侦察而言,正确识别雷达信号的调制方式不仅能够提高雷达信号的参数估计精度,还能推测雷达的功能,从而判断雷达的威胁等级。时频分析作为分析时变非平稳信号的有力工具,近年来,用其提取雷达信号脉内特征受到了越来越多学者的重视[1-4]。

信号的时频图像能直接体现出雷达信号脉内调制方式,那么雷达信号的脉内调制识别问题就可以转化为图像识别问题。奇异值分解(singular value decomposition,SVD)是图像特征分析常用的方法,具有鲁棒性好,位移旋转不变性,对噪声不敏感等优点[5]。奇异值熵能够反映奇异值大小分布情况,奇异值熵值越小,奇异值分布越均匀。文献[6]利用SVD去除雷达信号模糊函数图像的噪声,提高信号的识别率。文献[7-8]将信号时频图像的奇异值作为识别雷达信号特征,取得了不错的效果,但是特征维数较多,不利于分类器的分类识别。

雷达信号是一个时间序列,分形理论能对它的不规则度进行有效的刻画。信号的盒维数和信息维数能够反映信号几何形态的复杂度和疏密程度。文献[9-12]将从频域上提取信号的盒维数与信息维数作为雷达信号脉内调制方式识别特征,在信噪比较高时有不错的识别效果,但是信噪比较低时识别效果不佳。文献[13-14]从信号的双谱变换域内提取信号的盒维数和信息维数作为分类识别特征,再采用分类器实现了对雷达信号的分类识别,但是在低信噪比条件下识别效果仍然不佳。文献[15]证明了在低信噪比条件下信号的盒维数和信息维数稳定性不好,单独将其作为识别特征在低信噪比条件下是不可靠的。

本文针对低信噪比条件下雷达信号调制方式识别困难的问题,提出了将信号时频图像的奇异值熵特征和信号频谱的分形维数特征相融合,实现对雷达信号脉内调制方式识别的一种方法。该方法利用时频图像的奇异值熵对噪声不敏感的特征,保证算法的抗噪性;利用分形维数对信号的频谱形状能定量表示的特点,保证算法的识别率。

1 时频图像的奇异谱熵特征提取

1.1 Choi-Williams分布

信号的不同调制方式会在其时频图像上直接体现出来,获取时频图像的方法有:短时傅里叶变换(short-time Fourier tranform,STFT)、Wigner-Ville分布(Wigner-Ville distribution,WVD)、Choi-Williams分布(Choi-Williams distribution,CWD)等。STFT获取时频图像存在着窗函数宽度选取困难的问题,WVD虽然克服了STFT的缺点,但是其存在交叉项问题,而CWD克服了STFT和WVD的缺点,能够抑制和消除交叉项,并且有较高的时间分辨率和频率分辨率[16]。所以,本文选取CWD获取信号的时频图像。CWD的数学表达式为

CWDs(t,ω)=

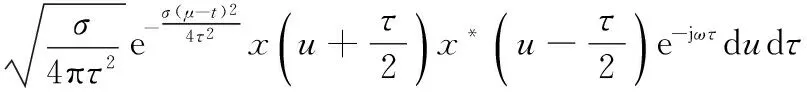
(1)

式中,σ为衰减系数,本文取σ=1。

图1给出了8种典型雷达信号的CWD的时频图像。8种信号分别为:线性调频(linear frequency modulation,LFM)信号、二相编码(binary phase shift keying,BPSK)信号、四相编码(quadrature phase shift keying,QPSK)信号、频率编码(frequency shift keying,FSK)信号、常规信号(normal signal,NS)、正弦调频(sinusoidal frequency modulation,SFM)信号、偶二次调频(even quadratic frequency modulation,EQFM)信号和COSTAS码调频信号。

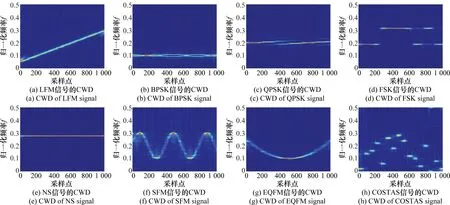
图1 8种雷达信号在信噪比为5 dB时的CWD时频图像Fig.1 CWD time frequency image of eight kinds of radar signal when SNR = 5 dB

1.2 奇异值分解与奇异值熵

将信号经过CWD变换得到的时频图像矩阵G进行奇异值分解,并求得奇异值熵。

实矩阵的SVD分解可以表示为

G=UDVT

(2)

奇异值分解具有下列特点[5]:①稳定,对于时频图像矩阵G的元素细微的变动,奇异值变化小,具有很好的稳定性;②具有旋转、位移、转置和镜像不变性。

不同信号的时频图像进行SVD后,奇异值的大小是不同的,奇异值能反映图像各个分量的占比,奇异值的个数与图像大小有关。文献[7]将奇异值归一化并提取十个最大奇异值组成特征向量,然后用分类器进行识别。这样将单一的奇异值特征存在如下问题:①同一种类型、不同参数的信号会使奇异值特征出现很大的偏差,导致识别效果变差,比如不同频率周期的SFM信号,不同码元宽度的BPSK信号和QPSK信号;②特征向量的维数太多,分析特征、训练模型所需的时间很长,并且特征个数过多,容易引起“维灾难”[17],从而影响分类器的识别。

图像的SVD可以理解为将图像的能量分布映射为奇异值大小分布,而奇异值熵就能够反映奇异值大小分布,故本文提出选取奇异值熵作为识别特征,奇异值熵表示奇异值的能量分布,奇异值熵越大,奇异值能量分布越不均匀,反之越均匀。奇异值熵可以理解为图像能量分布特征。图像的能量分布特征可以由那些较大的奇异值完全反映,在数据处理过程中,可以将较小的奇异值当做是噪声。所以本文提取奇异值熵特征时,选取前20个较大的奇异值,求这20个奇异值的奇异值熵。奇异值熵的计算公式为

(3)

式中,σi和M分别为奇异值和奇异值的个数。

2 分形维数特征提取

分形理论中有很多基本的分形维数,其中盒维数和信息维数因计算简单而广泛被应用。盒维数能够刻画几何形状的不规则性和复杂度,信息维数能描述几何形态的疏密程度。不同调制方式信号的波形和频谱是不同的,由于信号波形受噪声影响较大,频谱受噪声影响较小,所以,把信号频谱的盒维数和信息维数作为信号调制方式的识别特征是可行的。

2.1 盒维数

盒维数的定义为:设A∈F(X),F(X)为一度量空间,对每一δ>0,用Nδ(A)表示覆盖A的直径为δ的闭球的最少个数,如果

(4)

存在,则称DI为集A的盒维数。

一个长度为N的信号序列x(n)进行FFT,得到其频谱序列X(k)(k=1,2,…,N)。计算X(k)的盒维数采用简化算法[10]。将序列X(k)置于单位正方形中,横坐标的最小间隔δ=1/N,令

(5)

于是,盒维数的计算式为

(6)

2.2 信息维数

设{A(i)}(k=1,2,…,N)是集合F的有限δ-格型覆盖,Pi表示F中的元素落入A(i)中的概率,计算式为

(7)

式中,N(F)i和N(F∩Ai)表示元素的个数。令信息熵为

(8)

如果信息熵满足下面条件:

I(δ)=lgδDI(f)

(9)

那么,信息维数为

(10)

为了减少一些因素对信号盒维数和信息维数的影响,需要对信号进行预处理。预处理过程为:将信号变换到频域,得到信号长度为N个采样点的频谱序列X(i)(i=1,2,…,N),然后将信号幅度归一化,以消除信号强弱的影响。计算信息维数时,为了减少噪声的影响,采用下列方法重构信号并计算信息维数[10]:

Y(i)=|X(i+1)-X(i)|

(11)

式中,i=1,2,…,N。

令

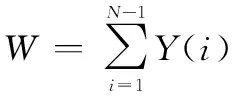
(12)

(13)

(14)

3 分类识别

将以上所述的3个特征组成特征向量S=(Hq,Db,DI),然后使用分类器进行分类识别。分类器采用基于标准支持向量机(criterion support vector machine,C-SVM)的分类器,这类分类器方法简单,需要的训练样本数少,分类效果好。

本文提出基于奇异值熵和分形维数的雷达信号识别算法的基本步骤如下:

步骤1将信号分别进行FFT和CWD变换,得到信号的频谱和时频图像;

步骤2将信号的频谱进行幅度归一化处理得到频谱序列X(k),将信号的时频图像进行幅度归一化处理得到了时频图像矩阵G;

步骤3为了减小噪声的影响,对时频图像矩阵进行简单的滤波,具体过程为:如果矩阵G中元素小于阈值,那么将其值置为零,根据仿真分析,阈值设为0.1～0.2是合适的,本文阈值设为0.15;

步骤4用式(6)和式(14)计算步骤2中信号频谱序列X(k)的盒维数Db和信息维数DI,对步骤3得到矩阵G进行奇异值分解,并求得前20个最大奇异值的奇异值熵Hq;

步骤5将步骤4中得到的3个特征组成特征向量S,再用C-SVM分类器分类识别。

4 仿真实验

仿真条件:仿真采用8种典型的雷达信号进行分类识别,分别为LFM、BPSK、QPSK、FSK、NS、SFM、EQFM、COSTAS。仿真信号采用归一化频率和带宽表示,雷达信号长度均为1 024个采样点,其中,LFM信号起始频率为0.1,带宽为0.1～0.35,BPSK信号采用13位巴克码,QPSK信号采用16位Frank码,NS信号的载频为0.05～0.4,FSK信号采用随机编码,SFM信号中心频率为0.2,带宽为0.1～0.4,EQFM信号最低频率为0.1,带宽为0.1～0.35,COSTAS信号采用16位COSTAS序列,信号附加噪声为高斯白噪声。对每一类雷达信号在-5～18 dB信噪比变化范围内,每隔1 dB产生100个样本,每类信号每个信噪比下拿出50个作为训练样本,剩下的样本作为测试样本。分类器采用C-SVM。

图2给出了不同雷达信号的奇异值熵随信噪比变化的曲线。从图2中可以看出信号的时频图像的奇异值熵随信噪比变化不大,具有很好的抗噪声性能,BPSK信号与EQFM信号、LFM信号与COSTAS信号奇异值熵比较接近,容易识别错误,而且在整个信噪比变化范围内,奇异值熵有重叠部分,因此,不能单独把信号时频图像的奇异值熵作为识别特征。从图3中可以看出在信噪比为4 dB时,奇异值熵、盒维数和信息维数这3个特征有较大的类间间距,有很好的可分性。图4给出了8类雷达信号在信噪比从-2 dB到18 dB范围内的三维特征分布图,可以看出,三维特征有很好的类内聚集性,只是在信噪比小于0 dB的条件下有类间重叠,这是因为信噪比小于0 dB时,信号的分形维数十分接近噪声的分形维数。

图2 8种雷达信号的奇异值熵随信噪比变化的曲线Fig.2 Singular value entropy of eight kinds of radar signal for different SNR

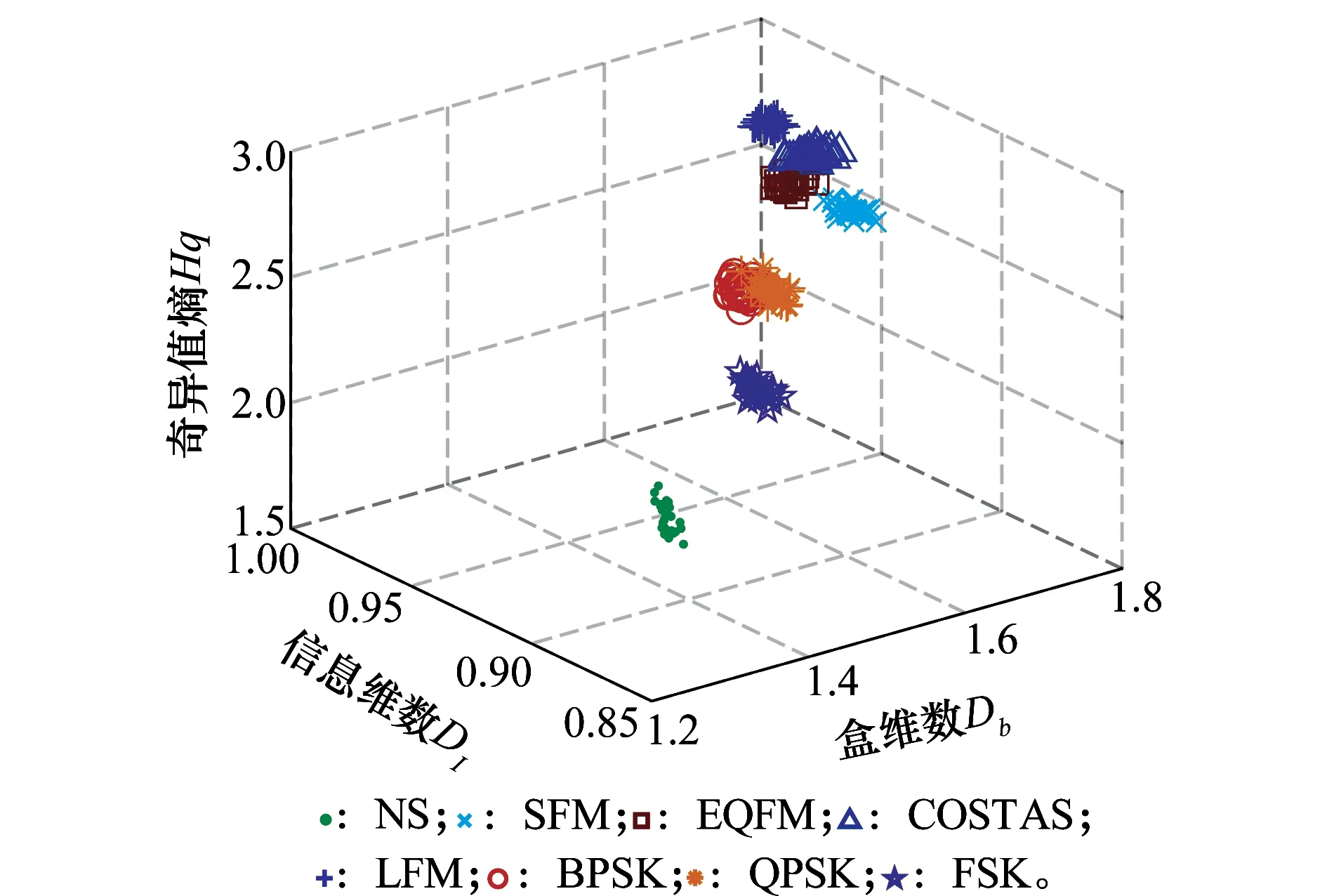
图3 信噪比为4 dB时不同信号的三维特征分布图Fig.3 Three dimensional characteristic distribution of different signals when SNR=4 dB

图4 信噪比从-2～18 dB时不同信号的三维特征分布图Fig.4 Three dimensional characteristic distribution of different signals when SNR from -2 dB to 18 dB

为了方便起见,下面将本文算法简称为SVEFD算法,分形维数算法简称为FD算法[9],基于奇异值分解的算法称为SVD算法[7-8]。图5是本文提出的基于奇异值熵和分形维数的雷达信号识别算法的识别效果图,从图5中可以看出,SVEFD算法在信噪比大于1 dB以上时,8类雷达信号的正确识别概率均能达到90%以上,信噪比大于4 dB时,8类雷达信号的正确识别概率达到了100%,说明SVEFD算法是有效的。

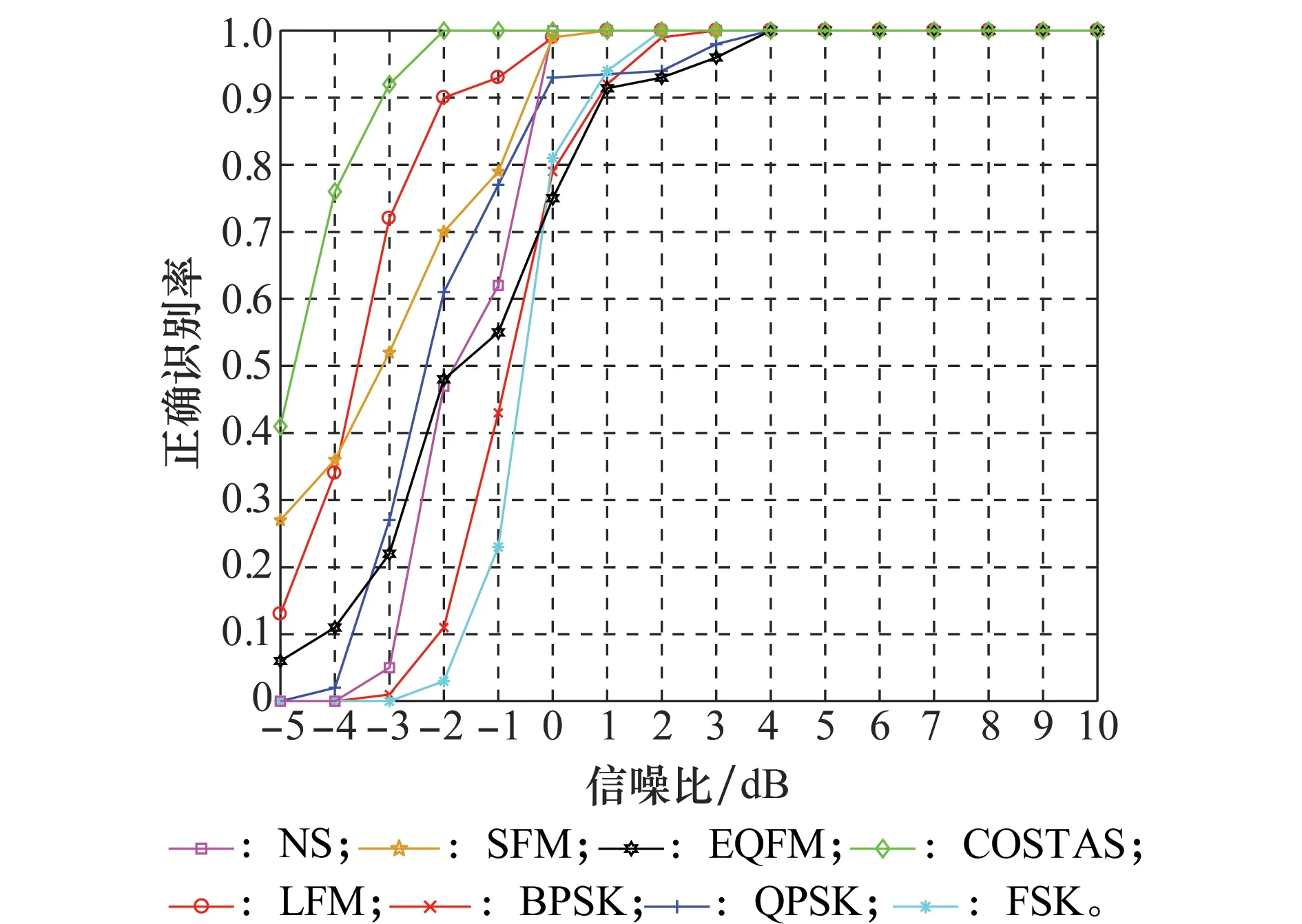
图5 SVEFD算法正确识别率Fig.5 Correct recognition rate of SVEFD algorithm

从图5中还可以看出,当信噪比为0 dB时,SVEFD算法对FSK、BPSK和EQFM 3种信号的正确识别率下降较快,低于90%。当信噪比为-1 dB时,SVEFD算法除了对LFM和COSTAS信号保持着90%以上的正确识别率外,其余六类信号正确识别率均很低。随着信噪比的进一步下降,SVEFD算法的性能下降很严重,这主要是因为信噪比在0 dB以下时,信号的时频图像矩阵和频谱受噪声影响较大,那么信号的奇异值熵和分形维数特征也受噪声影响很大,已不能作为信号的分类特征。这也是限制SVEFD算法抗噪声性能进一步提升的主要原因。

表1给出了FD、SVD、SVEFD 3种算法在信噪比大于-2 dB时8类雷达信号正确识别率,对比表1中的数据可以发现,SVEFD算法在较低信噪比下的正确识别概率远高于FD算法,也高于SVD算法,在信噪比大于1 dB时,平均识别率达到了95%,证明了本文的SVEFD算法是有效的。对比SVD算法,本文的SVEFD算法所需要的特征维数较少,分类和训练的时间短、运算量小,正确识别率较高。

表1 3种算法平均正确识别概率对比

5 结束语

本文提出了一种基于奇异值熵和分形维数的雷达信号识别算法,能够对雷达信号的脉内调制方式进行有效的识别。该算法通过提取信号时频分布图像的奇异值熵,结合信号频谱的分形维数参数,组成特征参数向量,送入分类器实现雷达信号调制方式的分类识别。计算机仿真结果表明,该方法抗噪性较强,在较低信噪比条件下,仍然具有很高的正确识别率。

[1] THAYAPARAN T, STANKOVIC L, AMIN M, et al. Editorial time-frequency approach to radar detection, imaging, and classification[J]. IET Signal Processing, 2010, 4(3):197-200.

[2] ZHU J, ZHAO Y, TANG J. Automatic recognition of radar signals based on time-frequency image character[J]. Defence Science Journal, 2013, 63(3):1-6.

[3] LIU Y J, XIAO P, WU H C, et al. LPI radar signal detection based on radial integration of Choi-Williams time-frequency image[J]. Journal of Systems Engineering and Electronics, 2015,26(5):973-981.

[4] ZHANG M,LIU L,DIAO M.LPI Radar waveform recognition based on time-frequency distribution[J].Sensors,2016,16(10):1682.

[5] 洪子泉, 杨静宇.用于图象识别的图象代数特征抽取[J].自动化学报,1992(2):233-238.

HONG Z Q, YANG J Y. Image algebraic feature extraction for image recognition[J]. Acta Automatica Sinica,1992(2):233-238.

[6] GUO Q, NAN P, ZHANG X, et al. Recognition of radar emitter signals based on SVD and AF main ridge slice[J]. Journal of Communications & Networks, 2015, 17(5):491-498.

[7] YANG L B, ZHANG S S, XIAO B. Radar emitter signal recognition based on time-frequency analysis[C]∥Proc.of the Radar Conference on IET Internationa, 2013:1-4.

[8] 龚文斌,黄可生.基于图像特征的雷达信号脉内调制识别算法[J].光电控制,2008, 15(4):45-49.

GONG W B, HUANG K S. An image-feature based methods for feature extraction of intra-pulse modulated signals[J]. Electronics Optics & Control,2008,15(4):45-49.

[9] 张葛祥, 胡来招, 金炜东.雷达辐射源信号脉内特征分析[J].红外与毫米波学报, 2004,23(6):477-480.

ZHANG G X, HU L Z, JIN W D. Intar-pulse feature analysis of radar emitter signals[J]. Journal of Infrared and Millimeter Waves, 2004,23 (6):477-480.

[10] YE F, YU Z F, LUO J Q. Analysis of Radar Emitter Signal Feature Based on Multifractal Theory[C]∥Proc.of the IEEE International Conference on Electronic Measurement and Instruments, 2007:1-14-1-17.

[11] MISHRA A K, FENG H, MULGREW B. Fractal feature based radar signal classification[C]∥Proc.of the IET International Conference on Radar Systems, 2007:1-4.

[12] LIN Y, XU X, PANG J. The improved recognition method of radiation signal under the condition of unstable SNR[J]. International Journal of Signal Processing Image Processing & Pattern Recognition, 2014(7):339-344.

[13] CHEN C, MINGHAO H E, JING X U, et al. A new method for sorting unknown radar emitter signal[J]. Chinese Journal of Electronics, 2014(3):499-502.

[14] 韩俊,陈晋汶,孙茹.复杂体制雷达辐射源信号识别新方法[J].雷达科学与技术, 2016, 14(1):76-80.

HAN J, CHEN J, SUN R. New method for recognizing complicated radar emitter signal[J]. Radar Science & Technology, 2016, 14(1):76-80.

[15] 吕铁军,郭双冰,肖先赐.调制信号的分形特征研究[J].中国科学:技术科学, 2001,31(6): 508-513.

LV T, GUO S, XIAO X. Study on fractal characteristics of modulation signal[J].Scientia Sinica (Technologica),2001,31(6):508-513.

[16] FENG Z, LIANG M, CHU F. Recent advances in time-frequency analysis methods for machinery fault diagnosis: A review with application examples[J]. Mechanical Systems & Signal Processing, 2013, 38(1):165-205.

[17] PIOTR I, RAJEEV M. Approximate nearest neighbors: towards removing the curse of dimensionality[J]. Theory of Computing, 2000(11):604-613.