基于线性校正的TOA联合同步与定位算法

田 强, 冯大政, 杨 凡, 胡豪爽

(西安电子科技大学雷达信号处理国家重点实验室, 陕西 西安 710071)

0 引 言

无线传感器网络定位技术在雷达、导航、目标跟踪和无线通信等领域[1-4]有着广泛的应用。多站目标定位是指处理中心利用多个传感器锚节点接收到的目标定位参数信息估计出目标节点的位置。常见的定位参数主要有:到达时间(time of arrival, TOA)、到达时间差(time difference of arrival, TDOA)、到达角度(angle of arrival, AOA)、信号到达强度(received signal strength, RSS)等[5-8]。

TOA定位技术利用目标信号到达多个传感器的传输时延来确定目标的位置,而传输时延的计算通常需要已知目标信号的发射时间,因此目标与传感器之间必须是精确同步的。然而在实际应用中,尤其对于非合作目标,目标与传感器之间往往存在时钟偏差。文献[9]的研究表明,即便是纳米级的时钟偏差都会严重影响传统TOA算法的定位精度。针对以上不同步的问题,目前主要有两种解决方法[10]:一是将传感器锚节点测量的TOA数据相减,消除未知的时钟偏差,转化为TDOA定位模型。然而,该方法会增加定位方程的非线性程度,而且减法处理会引入有色噪声,导致性能下降[11]。二是利用TOA测量数据对时钟偏差和目标位置进行联合估计。联合估计算法能够获得更高的定位精度,近年来受到了广泛的关注[12-16]。

联合同步与定位问题本质上是一个非线性、非凸的参数估计问题。利用最大似然估计(maximum likelihood estimator,MLE)能够得到非线性问题的渐进最优解,但需要进行格点搜索,计算量很大;通常的做法是利用泰勒级数(Taylor-series, TS)法[17]进行迭代求解,然而该方法需要一个迭代初始值,其收敛性过分依赖于初始值的选取,在初始值选取不好的情况下,很容易落入局部极小点,甚至出现发散的情况。文献[13]将原联合同步与定位问题转化为对二次方程的求解,有效避免了非线性运算,并且得到了目标位置和时钟偏差的闭式解;然而该算法只适用于目标位于传感器内部的情况,当目标位于传感器阵列的外部时,二次方程会出现多解甚至虚数解,对解的选取会严重影响算法的估计性能。文献[14]通过引入辅助变量克服非线性问题,并利用两步加权最小二乘(two-step weighted least square, TSWLS)算法得到了目标参数估计的解析解,该方法在测量误差较小时可以逼近克拉美罗下界(Cramer-Rao lower bound, CRLB),但测量误差较大时估计性能较差。近年来,一些学者引入凸优化方法[15-16],利用半正定松弛(semi-definite relaxation, SDR)技术,将目标函数转化为凸函数进行优化求解;然而由于松弛近似后的目标函数不再是紧的,因此该方法并不能得到最优解,而且优化过程计算量较大。

本文基于线性校正技术提出一种新的联合估计算法,该算法首先利用加权最小二乘理论得到目标参数的初始值,然后对初始值的偏差进行线性校正。与传统方法相比,该方法可以得到闭式解,同时又克服了传统闭式解方法中根的选取问题;在目标位于传感器阵列内部与外部两种情况下都可以逼近CRLB。理论分析和仿真实验证明了该算法的有效性。

1 定位模型

不失一般性,假设在二维平面内分布M个时钟相互同步的传感器锚节点,其坐标分别为si=[xi,yi]T,i=1,2,…,M;待测目标节点坐标为x=[x,y]T;目标节点与传感器网络是不同步的,假设时钟偏差为τ。根据TOA定位原理,目标信号到达第i个传感器的本地时间为

(1)

式中,‖si-x‖2表示目标x到传感器si的距离;c为光速;Δti为时间测量误差。

将式(1)两边同时乘c,可以得到

ri=cti=‖si-x‖2+τ+ni,i=1,2,…,M

(2)

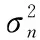
联合同步与定位问题就是利用方程(2)中的测量数据ri,同时估计出目标位置x以及时钟偏差τ。必须说明的是,为了简单起见,上述定位模型是建立在二维平面上的,但是文中算法很容易推广到三维空间中。

2 本文算法

2.1 加权最小二乘估计

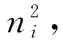
(3)

定义辅助变量η=xTx-τ2,同时令θ=[τ,xT,η]T,式(3)写成矩阵形式为

G1θ-h1=φ

(4)

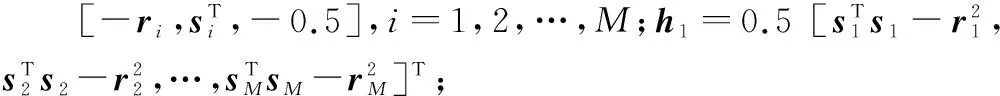
B=diag(‖s1-x‖2,‖s2-x‖2,…,‖sM-x‖2)

(5)

式(4)是关于θ的线性方程,根据加权最小二乘理论,可求出θ的解为

(6)

式中,加权矩阵W=E[φφT]-1=(BQnBT)-1,其中Qn为测量误差矢量n的协方差矩阵。需要说明的是，由式(5)可知,式中W的计算与目标真实位置x有关,而x是无法先验已知的。因此,在实际应用时,可先令W为单位阵I,求出式(6)的最小二乘解,然后再利用最小二乘解对W进行近似计算。

(7)

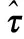
2.2 线性偏差校正

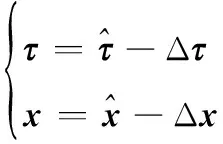
(8)

为了利用系统定位方程进行偏差校正,将式(8)代入式(3)中,经整理可得

(9)

式(9)的推导过程中忽略了二阶偏差项ΔxTΔx和Δτ2。

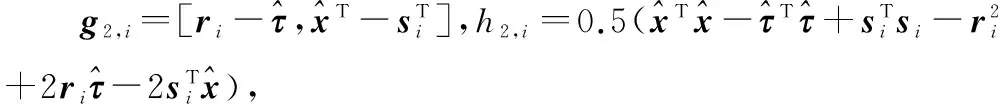
G2ξ-h2=φ

(10)

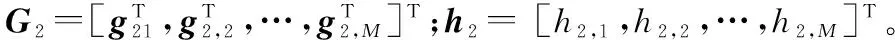
式(10)是关于偏差ξ的线性方程,其加权最小二乘求解为

(11)

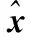
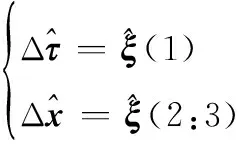
(12)

将式(12)代入式(8)中,则可以得到偏差校正后的目标参数估计为

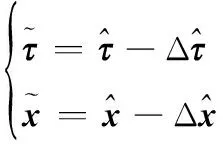
(13)

3 性能分析

对于任何无偏估计,CRLB确定了其参数估计误差协方差所能达到的下界,因此用其可以很好地评估本文所提算法的估计性能。根据文献[13]的研究结果,基于TOA的联合同步与定位问题的CRLB为

(14)

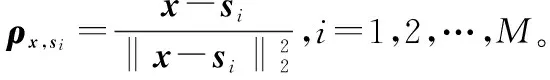
(15)

当测量误差较小时,由φ=Bn的定义可知,E[Δξ]=03×1,即线性偏差校正后的估计结果是近似无偏估计。

(16)

分别将G2和W的定义代入式(16)中,可得

(17)

当测量误差n充分小时,即满足

ni/‖si-x‖2≈0,i=1,2,…,M

(18)

时,由式(7)可知,加权最小二乘估计的偏差Δθ是测量误差n的线性组合,因此有近似

(19)

根据式(2)中TOA定位方程及式(8)、式(18)、式(19)的结果可得

(20)

将式(20)代入式(17)中,可得

(21)

根据以上分析可知,本文提出的基于线性校正的联合同步与定位算法,在测量误差较小时近似为有效估计。

4 实验仿真

为了验证文中算法的有效性,做了以下仿真实验,并将本文算法的估计性能与最大似然估计(maximum likelihood, ML)算法、文献[6]中的最小-最大算法(min-max algorithm,MMA)、文献[9]中的加权最小二乘(weighted least square, WLS)算法、文献[14]中的TSWLS算法以及CRLB进行了比较。

本文仿真实验在二维环境下进行,假定二维平面上有8个接收传感器,其坐标分别为

s1=[50,50]T,s2=[50,-50]T,s3=[-50,50]T

s4=[-50,-50]T,s5=[50,0]T,s6=[0,50]T

s7=[-50,0]T,s8=[0,-50]T

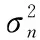
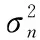
图1(a)和图1(b)分别为当目标在传感器阵列内部时,各算法对目标位置和时钟偏差的估计性能随测量误差变化的统计结果。从图1中可以看出,MMA算法的均方根误差始终偏离CRLB,这主要是因为MMA算法利用凸松弛技术,导致目标函数的约束条件不是紧的,造成性能损失,只能得到次优解。WLS算法、ML算法、TSWLS算法和本文算法的估计性能在测量误差较小时逼近CRLB;然而随着测量误差的增加,各算法的均方根误差都有所增加。其中,WLS算法比本文算法较早地出现门限效应;而ML算法的均方根误差急剧上升,这是因为当测量误差较大时,迭代初始值偏离真实值较远,导致算法局部收敛,甚至发散。此外,本文算法在测量误差较大时性能优于TSWLS算法,主要原因是,本文算法在第二步偏差校正过程中不仅利用了变量之间的函数关系而且充分利用了系统的原定位方程,因此提高了对测量误差容忍性。由图1可以看出,本文算法的估计均方根误差一直保持最小,估计性能优于传统方法。

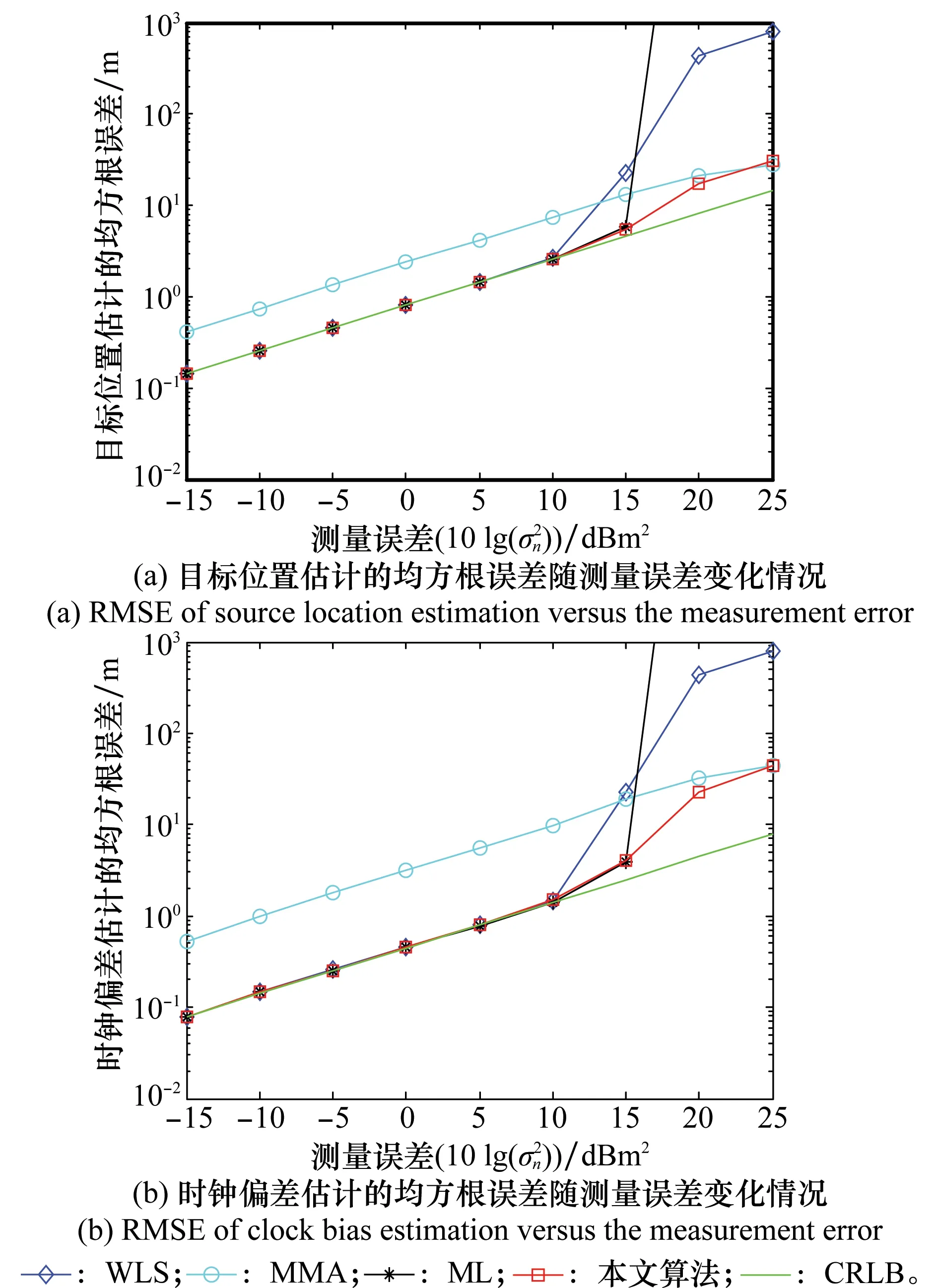
图1 目标位于传感器阵列内部时各算法的估计性能比较示意图Fig.1 Performance comparison of various algorithms for the source inside the sensor array

图2(a)和图2(b)分别为当目标在传感器阵列外部时,各算法对目标位置和时钟偏差的估计性能随测量误差变化的统计结果。从图2中可以得到与实验1类似的结论。但值得注意的是,在本实验的条件下,WLS算法的均方根误差始终偏离CRLB,当测量误差较大时,甚至出现了发散的现象,这主要是因为当目标在传感器阵列外部时,在WLS算法的二项式方程求根过程中出现虚数解,导致算法性能严重下降。在本实验条件下,本文算法与TSWLS算法性能近似,但根据图2中局部放大图可以看出,文中算法性能在测量误差较大时仍略优于TSWLS算法。而随着测量误差的增大,所有算法的性能均有所下降,而文中算法的均方根误差始终保持最低,具有较高的精度。

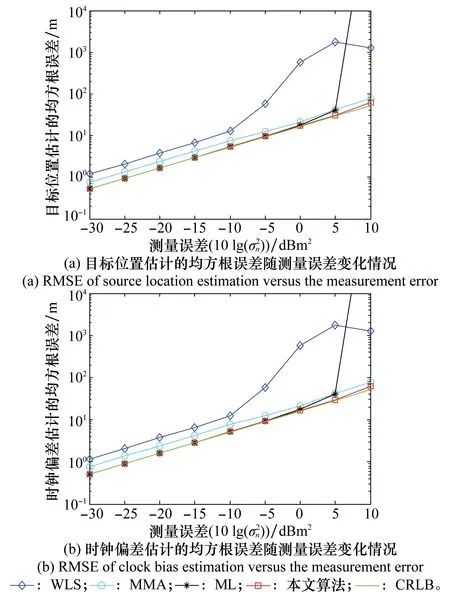
图2 目标位于传感器阵列外部时各算法的估计性能比较示意图Fig.2 Performance comparison of various algorithms for the source outside the sensor array

以上仿真实验结果与理论分析一致,文中算法在测量误差较小时能够逼近CRLB。从仿真结果可以看出,随着测量误差的增加,文中算法的性能优于传统方法,并且在目标位于传感器阵列内部和外部两种情况下都具有较高的估计精度。

5 结束语

针对传统TOA定位中目标与传感器时钟不同步的问题,提出了基于线性校正的联合同步与定位算法。通过对定位方程的线性近似,求出加权最小二乘解作为初始值,然后利用系统定位方程对初始值的偏差进行线性校正。理论分析了该算法在测量误差较小时为近似有效估计。实验结果表明,该算法性能优于传统的联合估计算法,对测量误差具有容忍性,在目标位于传感器内部和外部两种情况下都具有较高的定位与同步精度。

[1] SAYED A H, TARIGHAT A, KHAJEHNOURI N. Network-based wireless location: challenges faced in developing techniques for accurate wireless location information[J]. IEEE Signal Processing Magazine, 2005, 22(4): 24-40.

[2] DARDARI D, CLOSAS P, DJURIC P M. Indoor tracking: theory, methods, and technologies[J]. IEEE Trans.on Vehicular Technology, 2015, 64(4): 1263-1278.

[3] WIN M Z, CONTI A, MAZUELAS S, et al. Network localization and navigation via cooperation[J]. IEEE Communications Magazine， 2011, 49(5): 56-62.

[4] EINEMO M, SO H C. Weighted least squares algorithm for target localization in distributed MIMO radar[J]. Signal Processing, 2015, 115(C): 144-150.

[5] LIU C, YANG J, WANG F. Joint TDOA and AOA location algorithm[J]. Journal of Systems Engineering and Electronics, 2013, 24(2): 183-188.

[6] LIU C, FANG D, YANG Z, et al. RSS distribution-based passive localization and its application in sensor networks[J]. IEEE Trans.on Wireless Communications, 2016, 15(4): 2883-2895.

[7] LE T K, ONO N. Closed-form and near closed-form solutions for TOA-based joint source and sensor localization[J]. IEEE Trans.on Signal Processing, 2016, 64(18): 4751-4766.

[8] ZHU G H, FENG D Z, XIE H, et al. An approximately efficient bi-iterative method for source position and velocity estimation using TDOA and FDOA measurements[J]. Signal Processing, 2016, 125: 110-121.

[9] JEAN O, WEISS A J. Passive localization and synchronization using arbitrary signals[J]. IEEE Trans.on Signal Processing, 2014, 62(8): 2143-2150.

[10] VAGHEFI R M, BUEHRER R M. Asynchronous time-of-arrival-based source localization[C]∥Proc.of the IEEE International Conference on Acoustics, 2013: 4086-4090.

[11] PATWARI N, ASH J N, KYPEROUNTAS S, et al. Locating the nodes: cooperative localization in wireless sensor networks[J]. IEEE Signal Processing Magazine, 2005, 22(4): 54-69.

[12] ETZLINGER B, PIMMINGER C, FISCHEREDER S, et al. Passive localization and synchronization in the presence of affine clocks[C]∥Proc.of the 49th IEEE Asilomar Conference on Signals, Systems and Computers, 2015:1655-1658.

[13] ZHU S, DING Z. Joint synchronization and localization using TOAs: a linearization based WLS solution[J]. IEEE Journal on Selected Areas in Communications, 2010, 28(7): 1017-1025.

[14] HUANG J, XUE Y, YANG L. An efficient closed-form solution for joint synchronization and localization using TOA[J]. Future Generation Computer Systems,2013,29(3):776-781.

[15] XU E, DING Z, DASGUPTA S. Source localization in wireless sensor networks from signal time-of-arrival measurements[J]. IEEE Trans.on Signal Processing, 2011, 59(6): 2887-2897.

[16] WANG G, CAI S, LI Y, et al. Second-order cone relaxation for TOA-based source localization with unknown start transmission time[J]. IEEE Trans.on Vehicular Technology, 2014, 63(6): 2973-2977.

[17] FOY W H. Position-location solutions by Taylor-series estimation[J]. IEEE Trans.on Aerospace and Electronic Systems, 1976,12(2): 187-194.