基于CUDA的双二进制Turbo码并行译码方法
贾铁燕
(中国电子科技集团公司第五十四研究所,河北 石家庄050081)
0 引言
双二进制Turbo码是在DVB-RCS标准(ETSI EN 301 790 V1.5.1[1],以下简称790标准)中回传信道采用的前向纠错编码方式。Turbo 译码器采用2个SISO 软译码单元进行译码,2个 SISO 软译码单元在译码时要进行信息交互,不断在迭代中达到最大似然比[2-5]。对于双二进制Turbo码的译码算法,从性能上讲,最大后验概率[6](Maximum A Posteriori,MAP)算法是最优的,但是由于其存在大量的指数和乘法运算,复杂度较高,增加了实现的难度,Max-Log-MAP[7]算法在损失了一定性能的前提下对MAP算法进行了近似,可以降低一定的算法复杂度,从而更易实现。
Turbo码作为分组码,各分组间的译码算法可实现并行化,且单一分组内译码计算也存在可并行设计部分。目前Turbo码译码算法主要由FPGA实现[8-10]。随着集成电路的发展,原先仅用于加速图形计算的GPU 逐步应用于信号处理[11]。CUDA[12]作为NVIDIA 推出的运算平台,是一种通用并行计算架构,可使用C语言编写显示芯片上的执行程序。相对于FPGA实现更加灵活。本文提出了基于CUDA的对双二进制Turbo码的GPU并行加速译码方法。
1 编码原理
790标准的双二进制Turbo码编码器原理如图1所示,采用并行级联结构,由2个循环递归系统卷积码编码器(Circular Recursive System Code,CRSC)、1个随机交织器和1个删余器组成。对于码流输入顺序,最高有效位(Most Significant Bit,MSB)对应着A,最低有效位(Least Significant Bit,LSB)对应B。每一个分组长度中k比特或N比特对(k=2×N)。其中,N是4的倍数(k是8的倍数)。

图1 编码器原理[1]
双二进制Turbo码采用CRSC结构,反馈支路的多项式为1+D+D3,Y校验比特多项式为1+D2+D3,W校验比特多项式为1+D3。
图1中,3个寄存器状态定义为S1,S2和S3,则编码器状态定义为S,S=S1×4+S2×2+S3。
确定2个编码器的初始状态Sc1、Sc2的方法如下:
② 查表1确定Sc;
之后再使用Sc做初始状态进行编码,得到Y、W为校验位结果。
表1 循环状态对照表[1]

S0NN(mod7)012345671Sc=0Sc=6Sc=4Sc=2Sc=7Sc=1Sc=3Sc=52Sc=0Sc=3Sc=7Sc=4Sc=5Sc=6Sc=2Sc=13Sc=0Sc=5Sc=3Sc=6Sc=2Sc=7Sc=1Sc=44Sc=0Sc=4Sc=1Sc=5Sc=6Sc=2Sc=7Sc=35Sc=0Sc=2Sc=5Sc=7Sc=1Sc=3Sc=4Sc=66Sc=0Sc=7Sc=6Sc=1Sc=3Sc=4Sc=5Sc=2
双二进制Turbo码的交织器由二级组成,第一级进行输入比特对内部(A/B)的交织,第二级在比特对间进行交织。
定义默认交织参数P0,P1,P2和P3如表2所示。
表2 交织参数

分组长度(N对)P0{P1,P2,P3}4811{24,0,24}647{34,32,2}21213{106,108,2}22023{112,4,116}22817{116,72,188}42411{6,8,2}43213{0,4,8}44013{10,4,2}84819{2,16,6}85619{428,224,652}86419{2,16,6}75219{376,224,600}
对于第j对(j=0,1,…N-1)输入比特:
第一层交织:如果jmod 2=0,交换此比特对中A、B;
第二层交织:如果jmod 4 =0,则P=0;如果jmod 4=1,则P=N/2+P1;如果jmod 4=2,则P=P2;如果jmod 4=3,则P=N/2+P3。新位置i=P0×j+P+1 modN。
在790标准中,提到了7种速率的删余器:1/3,2/5,1/2,2/3,3/4,4/5,6/7。7种速率的删余图案[1]如图2所示。

1/3YW11[]2/5YW1110[]1/2YW10[]2/3YW1000[]3/4YW100000[]4/5YW10000000[]6/7YW100000000000[]
图2 删余图案(1表示保留)
2 译码原理
2.1 MAP及Max-Log-MAP算法


图3 译码器原理[13]
后验对数似然比:
lnP(uk|y)=ln(∑exp(Bk(s)+Γk(s′,s)+Ak(s′))),
式中,

外信息:
式中,Lc为信道的可信值,计算方法为:

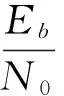
但是由于MAP算法存在大量指数和乘法运算,复杂度太高,不利于实现,于是采用了性能较好的Max-Log-MAP算法。Max-Log-MAP算法主要基于这样一种近似:
log(ex+ey)≈max(x,y)。
2.2 循环译码方法
由于DVB-RCS采用的是循环码,所以需要确定初始状态,采用环形译码可以消除这一影响。在算法初始化时,将所有状态取相同的初始度量,由于MAP算法可以在迭代中消除初始状态错误选择带来的影响,从第二次迭代开始,状态的初始度量取上次迭代时的度量值,即
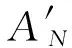
2.3 硬判决方法
对于满足迭代次数后的第二个SISO译码器输出的后验对数似然比,进行解交织送入判决器。对每一输入比特对y,根据后验对数似然比,取最大值即可得到最大可能的输入y,从而完成译码判决。
3 基于CUDA的并行译码方法
3.1 CUDA模型原理
CUDA是NVIDIA的通用计算图形处理器(General Purpose GPU,GPGPU)模型,使用C语言为基础。CUDA 的编程模型将CPU 作为主控制器,GPGPU 作为数据处理器即协处理器[14]。CPU 和GPGPU协同来完成任务[15]。在CUDA的架构下,一个程序分为两部分:host端和device端,host端是指在CPU上执行的部分,而device端则是在显示芯片上执行的部分。device端的程序又称为“kernel”。通常host端程序会将数据准备好后,复制到显卡的内存中,再由显示芯片执行device端程序,完成后再由host端程序将结果从显卡的内存中取回。
在CUDA架构下,显示芯片执行时的最小单位是thread(线程)。数个thread可以组成一个block(块)。一个block中的thread能存取同一块共享的内存,而且可以快速进行同步的动作。
每一个block所能包含的thread数目是有限的。但执行相同程序的block可以组成grid(格)。不同block中的thread无法存取同一个共享的内存,因此无法直接互通或进行同步。因此,不同block中的thread能合作的程度比较低。利用这个模式,可以让程序不用担心显示芯片实际上能同时执行的thread数目限制。
CUDA假设 CUDA 线程可在物理上独立的设备上执行,此类设备作为运行 C 语言程序的主机的协同处理器操作。例如,当内核在 GPU 上执行,而C语言程序的其他部分在 CPU 上执行时,就是这种情况。
此外,CUDA 还假设主机和设备均维护自己的动态随机存储器(Dynamic Random Access Memory,DRAM),分别称为主机存储器和设备存储器。因而,一个程序通过调用 CUDA 运行时来管理对内核可见的全局、固定和纹理存储器空间,包括设备存储器分配和取消分配,还包括主机和设备存储器之间的数据传输。
3.2 Max-Log-MAP译码算法的CUDA实现
实现高效的加速效果,关键在于CUDA 内部资源的合理分配:实验通过最大化并行线程的分配,以充分隐藏流水线延时[16]。为了解决Max-Log-MAP算法的并行化问题,设计了两级并行的译码算法。两级并行化设计实现了分组间并行与分组内并行,如图4所示。对于Turbo码这种分组码结构,各分组译码算法相互独立,利用并行化算法可以同时处理多个分组的译码,所以算法并行度至少为分组数。分组间并行实现,只需要将所有变量空间按分组数量进行扩展,各线程按自己所在分组,对所需变量空间的相应分组位置进行寻址即可。
对于一个分组,译码算法整个算法流程与图3相同,是由各子模块串行组成,各模块由于计算的类型不同,可并行度也有差别,最理想的情况是可全部并行处理,最差的情况为不能并行,即进行串行处理。将各模块单独进行并行化处理优化,根据自身的算法计算步骤,将相互无关联的计算进行并行算法设计,例如状态转移的路径权值可并行计算,而递归则不能并行计算。
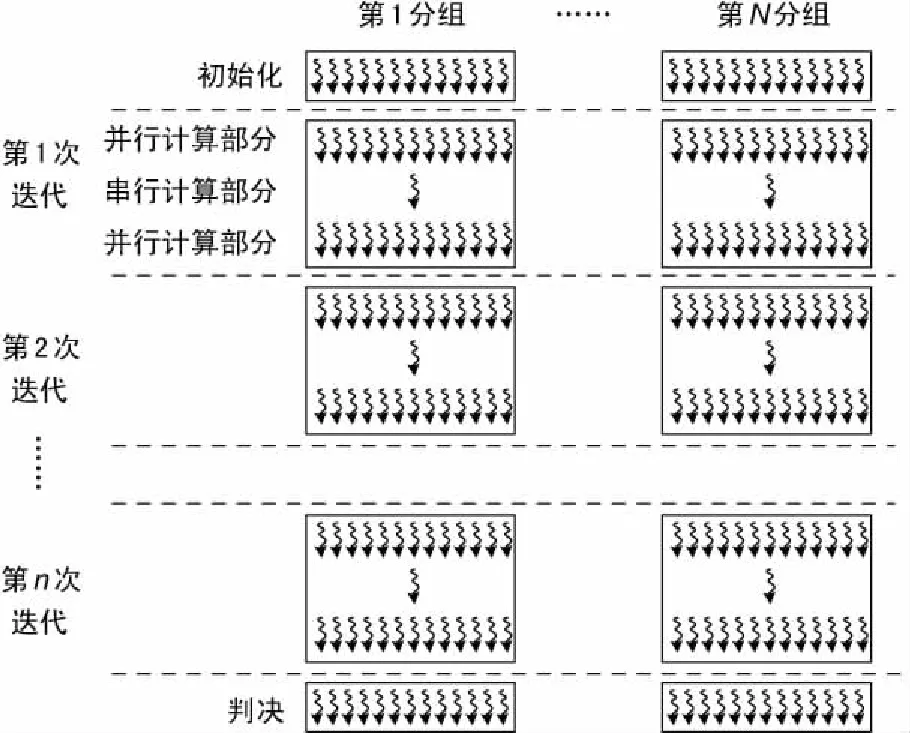
图4 Turbo码并行译码算法
交织器与解交织器的以一比特为并行单元。交织矩阵在程序运行阶段初在主机端计算完成,并复制到设备端。每一个thread对一个比特进行置换操作,该thread根据所处理比特所在分组和在分组的位置,并读取交织矩阵相应位置得到置换下标,进行置换操作。

分配每个thread完成一个s′到s状态转移的度量值计算,其中状态s共8种,输入共4种。为了方便代码书写,采用三维定义blockDim(partSize,8,4),第一维表示block完成输入比特对的数量,第二维表示当前状态,第三维表示第几种输入情况。所以这个kernel需要定义的gridDim大小为(分组数×分组长度/partSize)。

由于这是一个递归运算,所以同一分组中输入位之间的计算无法并行,而同一输入位的状态转移的度量值计算与求最大值操作是可以并行的。综上,分配一个二维thread,大小为(8,4),即s为8种,相应s′为4种,每一thread完成一个分组的所有输入位的相应s到s′的度量值计算。对于求最大值操作,采用二分法thread间协作并行处理。此kernel需要定义的gridDim即为分组数。
二分法计算如图5所示。

图5 8个点二分法计算示意
可以利用此法进行求和、连乘、最大值和最小值等运算。对于N个点需要进行ceil(lbN)次运算,即每次运算将所有点分成两组,每组对应两点进行计算。采用此方法,需要将所有点复制到block内的共享内存,即要保证所有数据不大于每个block的共享内存的最大值,且点数不能大于每个block最大并发线程数,并组在每一次计算后需要进行线程同步。
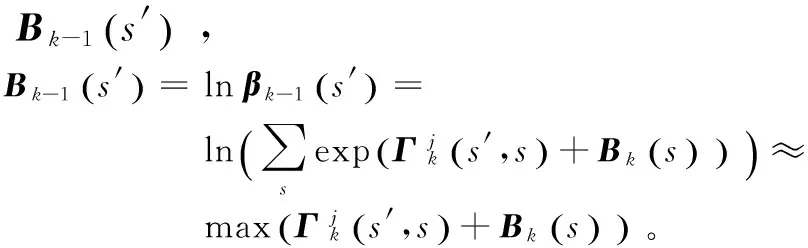

对于每一个输入位,计算是不相互独立的,分配一个二维thread,大小为(8,4),即s为8种,相应s′为4种,每一thread完成一个输入位的相应s到s′的度量值计算。此kernel需要定义的gridDim即为(分组数*分组长度)。

各输入位以及不同输入y的计算是相互独立的,可由每个thread单独完成。
硬判决器是根据后验对数似然比,得到取最大值的位置,从而完成译码。对于每一个输入比特对,相互之间计算是没有关联可并行的,且实际上完成的是求最大值位置的操作。由于输入只有4种,数量较少,该操作可并行度不高,这里直接由一个thread完成全部操作,无需thread间合作,代码依然采用二分法比较,可减少一次比较操作。
4 实验结果
实验在一个GPU工作站完成,配置如下:
CPU:Intel Xeon X5650@2.67GHz,
GPU:NVIDIA Tesla C2050。
实验了4种分组长度N下,在8次迭代时,对于分组平均译码时间,GPU加速后程序与CPU运行时间比,实现结果如表3所示。
表3 分组平均译码时间(8次迭代)

分组长度CPU运行时间/msGPU运行时间/ms运行时间比641.28070.051524.882124.28390.190122.534409.07960.449820.1986417.52500.879819.92
由实现结果可见运行速度提高了大约20倍,而且可以看出,分组长度最小,加速性能越好。这是因为在采用二分法设计时,分组长度越小,并行化率越高。
5 结束语
本文介绍了双二进制Turbo码的编译码算法,提出了基于CUDA的GPU并行计算加速译码算法。基于Max-Log-MAP算法,设计了GPU实现的方法 ,并给出了实现并给出了进行GPU加速前后的运算速度对比。实验结果表明,采用GPU加速后程序运行速度提高了大约20倍,说明该算法能够有效提高译码速度。
[1] ETSI EN 301 790 V1.3.1,European Telecommunication Standards Institute,Digital Video Broadcasting:Interactive Channel for Satellite Distribution Systems[S],2003.
[2] BENEDETTO S,DIVSALAR D,MONTORSI G,et al. Serial Concatenation of Interleaved Codes:Peorfmrnace Anyalsis. Design and Iterative Decoding[J].IEEE Trans.on inf.Theory,1999,44(3):909-926.
[3〗 ROBERTSON P.Illuminating the Structure of Code and Decoder of Parallel Concatenated Recursive Systematic (Tubro) Codes[J]. Proc.GLOBECOM,1994(12):1298-1303.
[4] PEERZL C, SEGHERS J,DNAIEL J,et al. A Distnace Specutrum Interpretation of Tubro Codes.Trnas.[J].IEEE Trans.on inf.Theory,1996,42(6):1698 -1709.
[5] 刘东华.Turbo码原理与应用技术[M].北京:电子工业出版社,2004.
[6] BAHLL R, COCKE J,JELINEK F. et al. Optimal Decoding of Linear Codes for Minimizing Symbol Error Rate[J]. IEEE Transaction on Information Theory,1974,IT-20(2):284-287.
[7] ERFANIANJ A, PASUPATHY S,GULAK G. Reduced Complexity Symbol Dectectors with Parallel Structures for ISI Channels[J].IEEE Transactions on Communications,1994,42:1661-1671.
[8] 祁栋生,陈自力,白勇博.Turbo码编码器的FPGA设计与实现[J]郑州轻工业学院学报,2010,25(6):115-117.
[9] 曾健平,张亦驰,李玉国.Turbo 编码的并行设计与优化[J].宇航计测技术,2010,30(2):75-78.
[10] 栗安定,陈寅健,胡豪,等.并行Turbo编码器[P].中国:ZL200910201488,2011.
[11] 成亚勇,闫冬,孙晓锋,等. 基于GPU实现的调频遥测解调方法[J].无线电工程,2016,46(4):35-38.
[12] 张舒,楮艳利,赵开勇,等. GPU 高性能运算之CUDA[M].北京:中国水利水电出版社,2009.
[13] ZHANC, ARSLAN T,ERDOGAN A T,et al. An Efficient Decoder Scheme for Double Binary Circular Turbo Codes[C]∥IEEE International Conference on Accoustics,Speech and Signal Processing,2006:IV-229-IV-232.
[14] 张喜明,陈旸.基于VPX标准总线的GPGPU平台的图像几何校正[J].无线电工程,2014,44(1):53-55.
[15] 傅丹,冯卫东,于起峰,等.一种摄像机自标定的线性方法[J].光电工程, 2008,35(1):71-75.
[16] 夏良正.数字图像处理[M].南京:东南大学出版社,1999.

