异型石材复杂曲线锯切加工算法研究

，玉厚， ，，，

(沈阳建筑大学机械工程学院,辽宁 沈阳 110168)

0 引言

圆盘锯片具有较大的刀具半径，在石材切削加工中能够获得更大的切削线速度和切削效率，因此被广泛应用于石材等硬脆材料的加工中[1]。

传统锯切加工，受制于锯片结构和工艺算法，主要用于直线加工。随着现代刀具技术和数控技术的发展，目前国外部分厂家已经将锯切用于复杂曲线、曲面加工[2]。Yamada提出用灵活的碗状圆形锯高速切割碳线纤维增强塑料(CFRP)的曲线加工[3-4]。文献[5-6]指出,碟形圆锯片所适宜的锯切半径取决于锯缝能否包容工件的相贯线。但是锯切加工在刀具结构、切削方式、运动路径和加工特性等方面与传统铣削、磨削存在较大差别[7-9]。

因此，尽管国内外目前出现了不少异型曲线锯切加工设备，但受制于对其加工工艺算法的研究不足，目前都没有被广泛应用[10]。对于石材复杂曲线、曲面的锯切加工，需要有新的运动控制算法。

1 锯切加工工艺

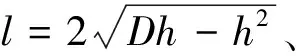
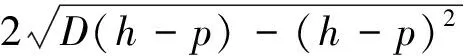
在锯切加工时，锯片以不同的刀触点和刀具位姿沿圆弧曲线进行切削加工时，其切削加工区间和切削加工特性存在很大差别。按照锯片结构，将刀触点位置分为前切点、中切点、后切点3种情况，如图1所示。

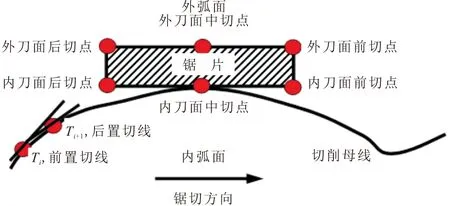
图1 锯切加工示意

当要求工件保留不同切削表面时，使用的刀具表面是不同的。当保留工件内弧面时，应该使用内刀面，此时的切削母线称为内弧线段；当保留工件外弧面时，应该使用外刀面，此时的切削母线称为外弧线段。因此，刀触点实际可分为6种情况，即：内刀面前切点；内刀面中切点；内刀面后切点；外刀面前切点；外刀面中切点；外刀面后切点。

当步长为t时，刀具位姿控制可以分为3种情况，即：前置切线法，刀具与ti相切；后置切线法，刀具与ti+1相切；中间切线法，刀具与ti和ti+1的中间点相切。由此可见，一共有18种锯切刀具控制算法，其切削量和切削加工特性各不相同，使用的场合也存在差异。这些算法主要就是根据目标曲线求出刀具的刀触点，根据步长和行距求出刀位点[11]，对锯片锯切曲线的控制，从而实现曲线锯切。

2 锯切加工算法

2.1 计算刀触点

锯片进行曲线切割的路径是以目标曲线用极坐标方程来描述，以2点间的的弧长设为进给量，弧长对应的圆心角为角度增量，角度变化的正负值来判断行进的方向，从而求出下一个刀触点的坐标。该曲线起于S1(X1,Y1)，终点为S2(X2,Y2)，当前刀触点为Pi(Xi,Yi)，下一刀触点为Pi+1(Xi+1,Yi+1)，如图2所示。

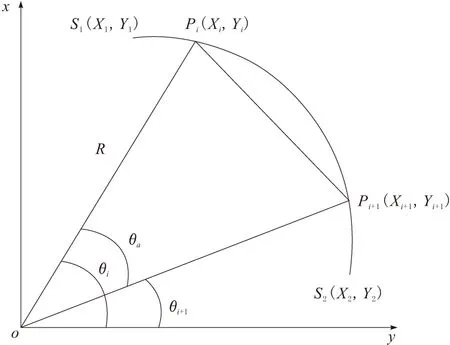
图2 曲线切割路径示意

圆弧PiPi+1所对应的弧长为ΔL，插补周期为Ts(ms)，进给速度F(mm/min)，因此该圆弧PiPi+1所对应的圆心角θa(rad)为：

(1)

对Pi和Pi+1用极坐标方程表示之间的关系为：

(2)

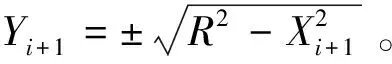
2.2 步长和行距

走刀步长是指锯片在同一条加工轨迹上的相邻2个刀触点之间的距离[12]，由于加工的路线一般都是一条复杂的曲线，而刀具移动的实质是数控系统对机床提供的插补运动而产生的。因此，在加工过程中刀具运动实际上是分解成由无数个分段的直线运动逼近曲线运动而形成的[13]，所以刀具运动的过程必然会产生逼近误差ε，刀具所走轨迹所在此处的法曲率半径为Ri，步长为Ls。由于曲线方程的最大曲率为K(θ)，由此得到最小的曲率半径Ri，则所求的加工曲线的最大步长Ls为：

(3)

加工行距是指刀具在相邻的2个加工轨迹上相对应的刀触点之间的距离[14]，一般与残留高度、刀具切削半径、曲线的曲率半径等有关。但是由于锯切加工的特殊性，在行距曲面连接处是抬刀处理，在通常加工环境下刀具有效半径为常数，残留高度由加工精度要求决定hs，那么加工行距Lw的值是由加工曲线的曲率参数ρ决定的，当ρ→∞时，加工曲线可看做为直线，所以Lw可简化表示为：

(4)

2.3 计算刀位点

由刀触点曲线按某种刀具偏置计算方法生成刀具轨迹曲线叫做刀位点路径[15-16]，在此采用的刀具为圆锯片，采用它的圆心为刀位点。锯片的半径为R，曲面上任意一刀触点Pc=r(u,v)，因为锯片在锯切的过程中根据刀具左右偏置情况，sign(det[ru,rv])为1[17]，所以刀位点Pt简化为：

(5)

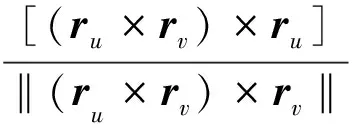
内弧线段切割时，要求保留弧线以内的区间，距离切削母线曲率中心最近的切削点是决定切削表面形貌的关键。刀具与切削母线不相切，前切点控刀；刀具与切削母线相切，中间点控刀。外弧线段切割时，要求保留弧线以外的区间，切削母线曲率大于刀具半径，刀具前后切点与切削母线重合，切削母线曲率小于刀具半径，需要刀具前切点控刀。

3 过渡曲线锯切加工

加工单一的曲线时锯片的控刀方式可以不变，在加工过程中需要加工过渡区域的曲线，也就是在加工如图3所示从凸圆弧运动到凹圆弧的位置时，就需要考虑倾斜锯片的角度了。理论上锯片的控制点是从C到E的轨迹运动，但是中间从凸圆弧过渡到凹圆弧要考虑锯片绕到另一侧的问题，也就是说锯片绕C轴转到凹圆弧的一侧。由于凸圆弧和凹圆弧是不同的，换句话说是从外圆弧加工到内圆弧，为了防止内圆弧过切现象的发生，锯片也要绕A轴倾斜角度以保证加工顺利进行。

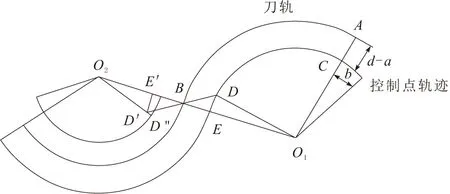
图3 圆弧过渡

对于五轴机床的锯片安装中心相对于机床控制点存在一些偏置[18]，如图4所示。在X轴方向上，C轴轴线与锯片轴线偏置为b；在Y轴方向上，A轴轴线与C轴轴线偏置为a，A轴轴线与锯片中心偏置为d；在Z轴方向上，A轴轴线与锯片轴线偏置为c；锯片的半径为e。在实际加工中，这些偏置或多或少的影响加工效果，所以也需要对这些偏置进行一些补偿处理[19]。

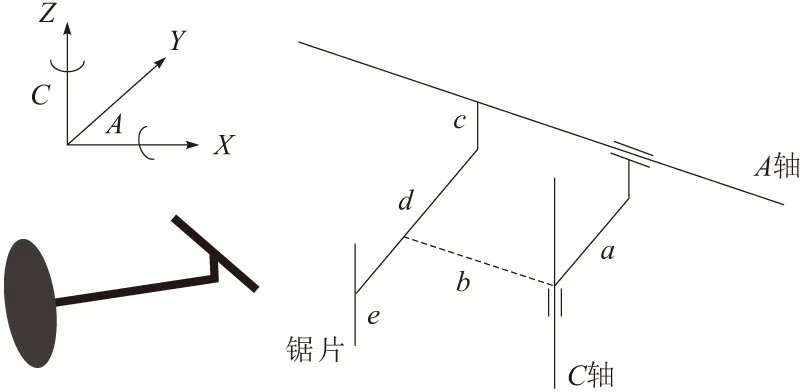
图4 锯片具有的偏置

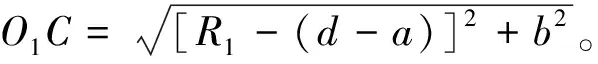
图5 同心圆的几何关系

在凸圆弧过渡到凹圆弧时，锯片绕C轴旋转180°,并且预防过切现象的发生控制点要修正到D′点，因为是凹圆弧锯片绕A倾斜角度。这个角度可以通过几何关系求出来。因为锯片与加工图形所构成的弦长相等，因此可求解得：

(6)

绕A轴倾斜后，接触点会由A移动到A’，它移动的轨迹是一条弧线，如图6所示，相应的控制点也会向前移动。因此控制点在凹圆弧加工半径方向上的距离数值上与AD的距离相等，该距离为：

(7)

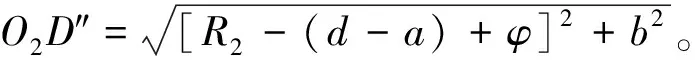
图6 移动轨迹及所具有的关系

综上所述，锯片在加工到凸凹圆弧相连的位置时，通过改变控制点的半径以及倾斜角度的调整来保证锯片正确连续工作。

4 刀具能够切削的最小曲率

极坐标系中目标曲线的曲率可以表示为：

(8)

根据曲线的斜率，通过对比锯片刀具所能加工的最小曲率选取不同规格的锯片，然后采用不同的控刀方式。

5 过切判断与处理

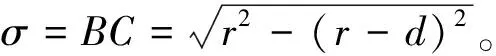
因此，用锯片在加工工件时，需要对图形的端点进行提前的修正补偿处理，消除锯片过切的影响[20]，达到正确的加工效果和减小误差。如图8所示，图形ABCD为理论加工路线，当刀位点走到ABCD点时，AA′，AA″是锯片的过切部分，同理图8中虚线部分为过切部分，所以消除过切现象是至关重要的。

例如，锯片在加工到如图9所示的位置时，预防过切现象要做保留加工，把图中的B，C，D刀触点点坐标做更改。 由于过切部分的长度为σ，需要更改的坐标为(x，y)。图中直线的倾角为θ，具体公式为：

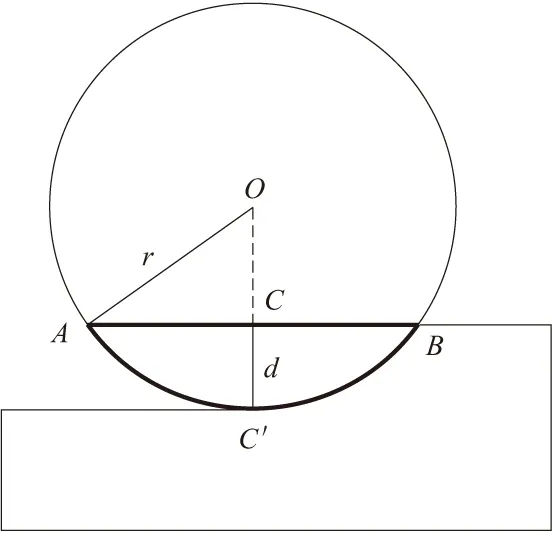
图7 过切长度

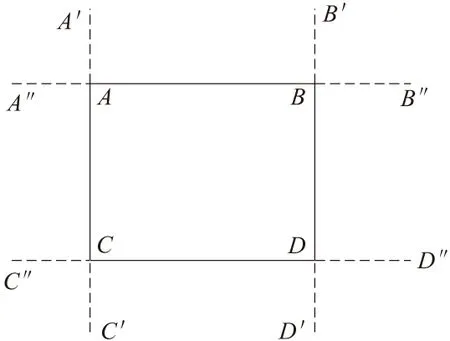
图8 过切部分

(9)

(10)

(11)

(12)

θ为直线倾角，当线段的斜率不存在，上端点用式(9)修正更改，下端点用式(10)修正更改；斜率存在，左端点用式(11)修正更改，右端点用式(12)修正更改。

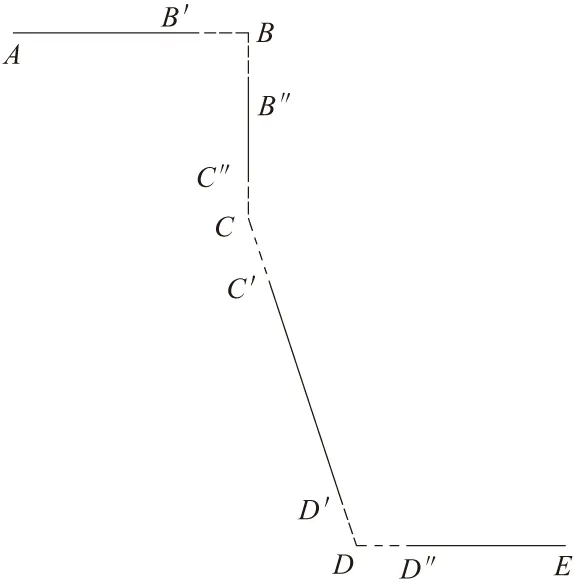
图9 过切处理

6 异型曲线锯切加工实验验证

经过对锯片加工的理论分析，在实现仿真时首先用Pro/E画出锯片所要切出的模型，然后导入PowerMILL进行加工仿真，在PowerMILL中建立用户坐标系并且激活，添加毛坯和刀具等，如图10所示。

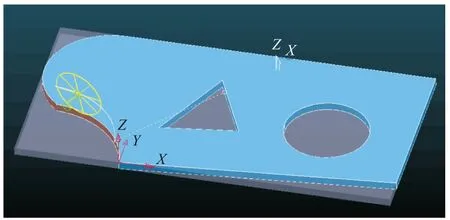
图10 生成毛坯

对于在加工过程中所要预防过切现象需要根据过切长度提前抬刀，所生成的刀具路径，在加工曲线段时锯片对绕着X轴转的A轴倾斜角度的效果如图11所示。

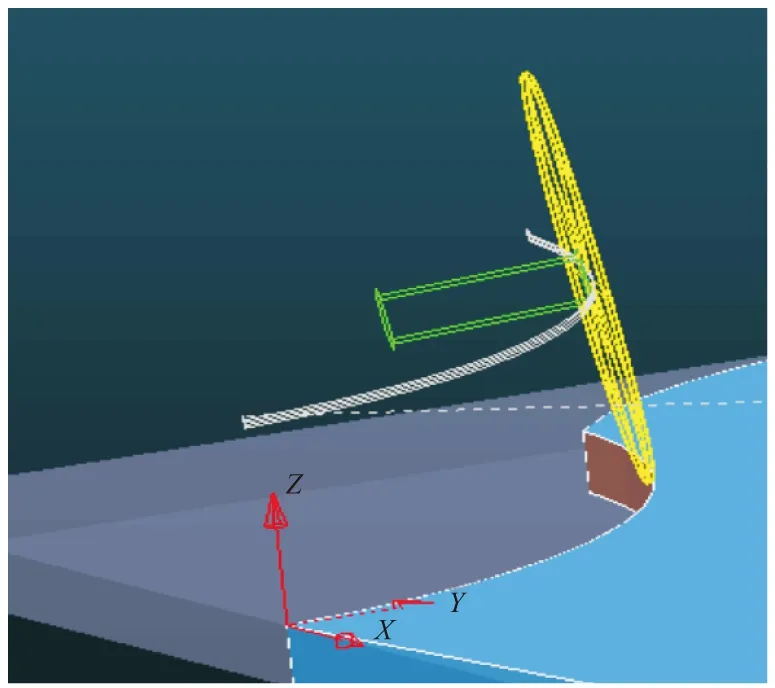
图11 锯片绕A轴倾斜

通过仿真实验发现，加工凸曲线曲率为0.002，锯片半径为400 mm时，锯片的倾斜角度在0～15°之间可以生成刀具路径。选取锯片倾斜0°，倾斜8°，倾斜15°时的数据，锯片在倾斜不同角度的情况下仿真出来的效果也不一样，锯片倾斜不同角度所产生的影响如表1所示。

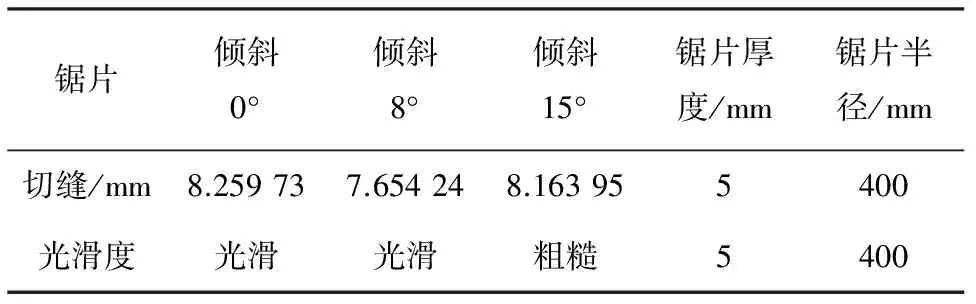
表1 锯片倾斜产生的影响

最终仿真结果如图12所示。图中三角形区域经过预防过切处理得到的完整无误的图形，其他区域由于是产生的废料，所以没有做预防过切现象的处理。

将本算法应用在异型石材五轴锯铣加工中心当中，加工出来的大理石石材产品的扇形弧面如图13和图14所示，加工出来的产品质量良好，轮廓清晰，证明该算法在异型石材曲线锯切方面有效可行。

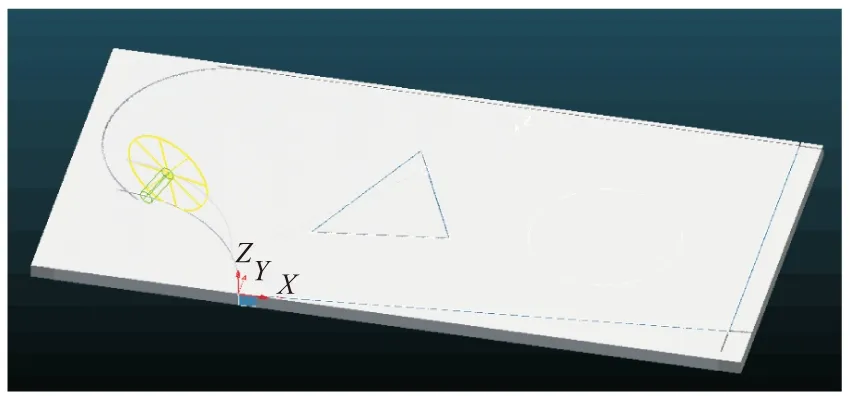
图12 完整效果

图13 加工产品

图14 加工产品

7 结束语

根据所研究的锯切算法，锯片在需要过切处理时，通过提前抬刀对工件过切现象的处理有效，具体的抬刀点和锯片所要加工的深度有关，而且通过提前抬刀的方式保证了工件的完整性和连续性。

锯片在进行曲线切割时针对相同曲率曲线，对于本文锯片需要绕A轴倾斜的角度是0～15°，超过这个范围锯片生成不了刀具路径，无法完成加工。

锯片在进行曲线切割时，锯片倾斜的角度不同，加工出来的质量也不一样，在此，锯片倾斜8°时加工出来的质量最好。

[1] 张云才,胡欢. 金刚石圆锯片基体在石材切割中如何做到更薄、更多、更大[J]. 石材,2017(9):22-26，32.

[2] 蔡锐龙,李晓栋,钱思思. 国内外数控系统技术研究现状与发展趋势[J]. 机械科学与技术,2016,35(4):493-500.

[3] Yamada Y, Osumi N, Takasugi A, et al. Curved-line cutting using a flexible circular saw[J]. Journal of Advanced Mechanical Design, Systems and Manufacturing, 2012, 6(6): 971-978.

[4] Yamada Y,Sasahara H.Free-form curves cutting using flexible circular saw[J].Precision Engineering,2014,38(3): 611-616.

[5] 颜连涛. 石材异型制品复合加工工艺及设备研究[D].济南：山东大学,2012.

[6] 袁杰. 石材异型制品复合加工技术与设备研究[D].济南：山东大学,2008.

[7] 赵玉刚,张健,于光伟,等. 异型石材成形加工刀具工艺的研究[J]. 机床与液压,2010,38(24):20-22.

[8] 刘岩. 数控五轴联动加工在异型石材中的应用研究[D].沈阳：沈阳建筑大学,2013.

[9] Wu B,Yan X,Luo M,et al. Cutting force prediction for circular end milling process[J]. Chinese Journal of Aeronautics,2013,26(4):1057-1063.

[10] Bao P,Luan F J,Zhang K,et al. Algorithm research of profiled surface stones sawing processing algorithm on digital[C]//Proceedings of 2014 International Conference on Advanced Control, Automation and Robotics (ACAR2014)，2015:372-379.

[11] 王迎春. 数控加工中截面线法刀具轨迹的生成与仿真研究[D].沈阳：沈阳工业大学,2003.

[12] 姬俊锋,周来水,安鲁陵,等. 考虑非线性误差补偿的五坐标数控加工走刀步长改进算法[J]. 重庆大学学报,2010,33(4):37-42.

[13] 籍亚红. 自由曲面数控加工中的刀具路径规划[D].沈阳：沈阳工业大学,2008.

[14] 张蕾. 基面曲线导向复杂点云数控加工路径生成方法[D].大连：大连理工大学,2016.

[15] Cai Y L,Zhao M B.Cutter location point calculation for five-axis surface machining with ellipse cutter[J].International Journal of Production Research,2014,52(2):436-444.

[16] Chen W T,Xia F C,Tu H N.Algorithm research of cutter location path for five-axis NC machining based on equal-parametric[J].Applied Mechanics and Materials,2012,(128-129):54-57.

[17] 吴玉厚,赵德宏,闫广宇. 基于刀触点路径截面线法的不规则曲面锯切加工算法研究[J]. 大连理工大学学报,2017,57(4):352-359.

[18] 游银涛,陈永明,刘康. 五轴石材切板机床刀具补偿算法的研究[J]. 机电工程,2016,33(1):63-67.

[19] 张导成. 数控铣削中半径补偿产生过切的原因及对策[J]. 装备制造技术,2009(4):127-129.

[20] 甘星明. 基于RS274/NGC的数控系统刀具补偿的设计与实现[D].沈阳：中国科学院研究生院(沈阳计算技术研究所),2006.