履带式爬壁机器人磁吸附单元优化设计与实验研究
,, ,,,3, ,3
(1. 南华大学机械工程学院,湖南 衡阳 421001;2. 中国科学院深圳先进技术研究院精密工程中心,广东 深圳 518055;3. 中国石油大学化学工程学院,北京 102249)
0 引言
爬壁机器人作为特种机器人的分支,能够代替工人通过携带清洗工具,在船舶垂直壁面上执行除锈任务[1]。既能提高除锈效率,又能保障工人们的人身安全,是船舶修理企业迫切需要的一种自动化机械装置,引起了研究人员的广泛关注。
为了适应不同的作业壁面,爬壁机器人有多种吸附方式。常用的吸附方式主要有永磁吸附、真空吸附等。永磁吸附具有吸附力可靠、壁面适应力强等特点;而真空吸附则需要保持吸盘内真空,要求壁面平整[2]。而船舶壁面凹凸不平,不适宜采用真空吸附。因此,爬壁机器人采用永磁吸附更为可靠。
吸附单元作为行走机构的核心部分,为在垂直壁面正常行走的爬壁机器人提供吸附力保证。因此,吸附单元结构的合理设计是爬壁机器人正常工作的前提。在此,通过建立三维理论模型,运用有限元方法,对磁吸附单元的结构参数进行定量分析,得到各个参数与吸附力之间的变化规律。同时,运用多因素分析的方法,对主要参数进行了优化分析,在体积保持不变的前提下,吸附力有了显著提高。
1 磁吸附单元基本结构参数
1.1 基本结构
爬壁机器人采用履带行走方式,磁吸附单元绕链条等间距镶嵌。为了提高爬壁机器人轻量化程度,磁吸附单元的结构设计应遵守体积小、质量轻等原则。吸附单元由2块磁铁组成,为了保护磁铁不被碰损,由橡胶套包覆磁铁,与铝框一起安装在轭铁上。结构布置如图1所示。
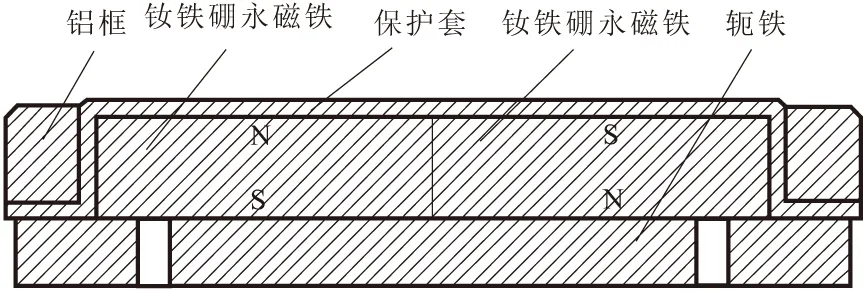
图1 磁吸附单元的结构
1.2 永磁材料的选择
履带上镶嵌了28块磁吸附单元,每块永磁铁应保证选用的永磁材料单位体积储磁能量大且性能稳定。为了满足这一要求,永磁铁选用钕铁硼N48H材料,它具有较高的矫顽力和磁能积,并且耐高温。钕铁硼的最大磁能积、剩磁和内禀矫顽力参数的值越大,磁性就越好[3]。钕铁硼N48H的性能参数如表1所示。

表1 烧结钕铁硼N48H性能参数
2 建立三维静态磁场理论计算模型
Ansoft Maxwell 软件采用的三维静磁场计算主要以剖分单元边上待求解量为自由度运算,即棱边法,对静态电磁场进行求解。麦克斯韦方程组、介质的本构方程和边界条件是静态磁场的求解依据[4-6]。因此,可以得到三维磁场下的麦克斯韦静态磁场数学模型,如式(1)和式(2)所示。
×H(x,y,z)=J(x,y,z)
(1)
(2)
H(x,y,z)为磁场强度,J(x,y,z)为传导电流密度,B(x,y,z)为磁感应强度,这3个矢量分别是3个方向矢量函数关系,如下式所示。
(3)
Bx,By,Bz为3个方向上的标量磁感应强度。
永磁铁采用N48H永磁材料,轭铁采用Q235导磁材料,介质为空气。由于上述材料都属于各项同性材料,因此符合关系式B=μ0H,其中μ0为空气的磁导率。为了方便运算,引入辅助矢量A,则有:
B=×A
(4)
式(4)中A为定值,根据库伦规范可得:
·A=0
(5)
由式(4)和式(5)可得:
×A)=J
(6)
将式(6)在三维直角坐标系中展开,得到:
(7)
式(7)中,部分参数为:
(8)
根据式(4)得:
(9)
Ax,Ay,Az,Bx,By,Bz,Jx,Jy,Jz分别为A,B,J在三维坐标系中的x,y,z方向上的分量。根据上述理论模型,以及实际磁路结构和边界条件,即可求出磁场参数。
磁场分析的目的是为了计算出吸附单元与壁面间的吸附力,根据麦克斯韦张力法,可以得到作用在壁面上的磁吸附力为[7]:
(10)
T为张力张量;μr为相对磁导率;S为包围在磁场空间中的介质的闭合面;B为闭合面任意处的磁感应强度;n为闭合面任意位置的外法向方向的单位矢量。
上述理论模型是进行有限元磁路仿真计算的根本依据。由式(10)可知,利用Ansoft Maxwell软件进行磁路仿真时,必须设置好仿真模型的边界条件和激励源。
3 吸附单元的磁路仿真与结构优化设计
3.1 磁路仿真
磁路设计是影响吸附力大小的关键因素,为了进一步提高永磁体的利用率,降低漏磁系数,磁路结构采用乙型磁路设计。为了验证乙型磁路设计的合理性,对吸附单元的结构进行了磁路仿真。
通过Ansoft Maxwell软件,建立三维模型,添加对应的材料参数,设置好激励源和边界条件,运用有限元方法对磁吸附单元进行磁路仿真,得到的磁吸附单元矢量磁密分布图,如图2所示。
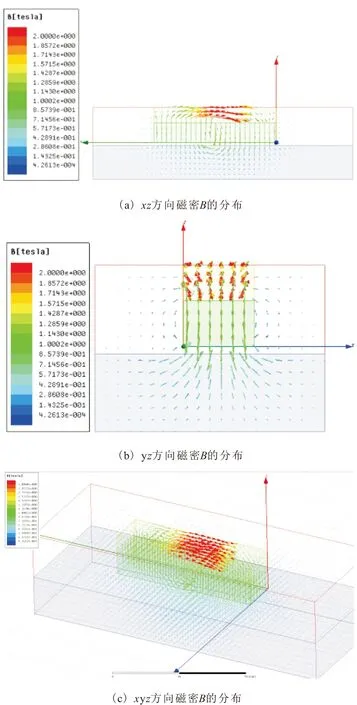
图2 磁吸附单元矢量磁密B的分布
由图 2中显示的矢量磁密B的分布趋势可以看出,磁吸附单元的磁密B基本都是Bx和By分量,Z轴方向的分量非常小,同时磁吸附单元呈现4个磁极分布,这些都符合乙型磁路设计原理和实际用途。
3.2 关键参数设计研究
吸附单元主要由2块永磁体和1块轭铁组成,形成乙型磁路,结构如图3所示。图3中,L为永磁体长度,W为永磁体宽度,H为永磁体高度,h为轭铁高度,g为橡胶套的厚度(磁铁与壁面的间隙)。

图3 永磁吸附单元的尺寸参数
由文献[8]可知,当钢板面积超过吸附单元面积一倍以后,钢板的面积对吸附单元的影响越来越小,符合实际工作状态,基本可以忽略。为了既能满足装配关系,又能准确地研究各个尺寸参数与吸附力之间的变化规律,通过文献[9],初步设计了方案1。通过仿真分析,得到最大吸附力为504 N,其结构参数如表2所示。

表2 方案1吸附单元结构参数 mm
3.2.1 橡胶套的厚度g对吸附力的影响
在方案1的基础上,保持吸附单元体积不变,运用定量分析法,对橡胶套厚度g进行分析。关键参数分别为L=50 mm,W=20 mm,h=15 mm,钢板的面积和厚度保持不变。通过建立优化变量参数g,取值范围设为0~8 mm,间隔为0.5 mm,对其进行求解。通过处理仿真数据,得到吸附力F与橡胶套厚度g的变化规律,如图4所示。

图4 吸附力F与橡胶套厚度g的变化规律
由图4可以看出,随着橡胶套厚度g不断增大,吸附力F却逐渐缩小,呈线性变化关系。从0 mm到8 mm范围内,吸附力F从988.2 N衰减到160.7 N,衰减速率较快。因此可知,橡胶套的厚度g对吸附单元的吸附力F影响较大。
3.2.2 磁铁长度L对吸附力的影响
同理,取W=20 mm,h=15 mm,g=2.5 mm,L为变量参数,取值范围为10~70 mm,等间隔为5 mm,对其进行求解。通过处理仿真数据,得到吸附力F与磁铁长度L的变化变化规律,如图5所示。
由图5可以看出,吸附力随着永磁单元长度的增加而增大,近似呈正比例关系。在10~50 mm区间,吸附力F由15 N增加至504 N,吸附力增加了32.6倍,增长速率较快。由此表明,这一区间,永磁体长度L对吸附力F的影响较大。在50~70 mm区间,吸附力从504 N增加至617 N,增加了0.22倍,增长速率逐渐放缓,永磁单元长度L增加对吸附力F的影响偏小一些。

图5 永磁体长度L与吸附力F的变化规律
3.2.3 永磁体宽度W对吸附力的影响
同理,取L=50 mm,H=15 mm,g=2.5 mm。建立优化变量参数W,取值范围为2~26 mm,等间隔为2 mm,对其进行求解。通过处理仿真数据,得到吸附力F随永磁体宽度W的变化规律,如图6所示。

图6 永磁体宽度W与吸附力F的变化规律
由图6可以看出,吸附力F随着永磁体宽度W增加而增大。宽度由2 mm增加到26 mm,吸附力由11.6 N增加至673.2 N,增加了57倍,同时体积也增加了13倍。结果表明,永磁体宽度W对吸附力F的影响较大。但考虑到装配关系,永磁体宽度与长度的比值应小于1。
3.2.4 永磁体高度H对吸附力的影响
同理,取L=50 mm,W=15 mm,g=2.5 mm。建立优化变量参数H,取值范围为5~20 mm,等间隔2 mm, 通过处理仿真数据得到吸附力随永磁体宽度的变化曲线,如图7所示。
由图7可以看出,吸附力随着永磁体高度增加而增大。高度由2 mm增加到20 mm时,吸附力由151.4 N增加至559.1 N,增加了2.69倍,体积增加10倍,对吸附力影响较大。当永磁体厚度大于宽度时,对吸附力的影响变小,直至不会产生影响。
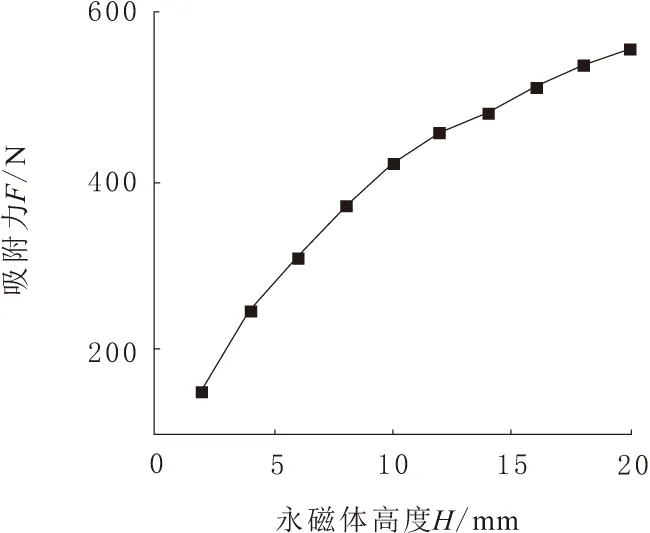
图7 永磁体高度H与吸附力F的变化规律
3.2.5 轭铁高度h对吸附力的影响
同理,取L=50 mm,W=20 mm,H=15 mm,g=2.5 mm。建立优化变量参数h,取值范围为5~20 mm,等间隔2 mm, 通过处理仿真数据得到吸附力F随轭铁高度h的变化曲线,如图8所示。

图8 轭铁高度h与吸附力F的变化规律
由图8可知,吸附力随着轭铁高度的增加而不断增加。高度由2 mm增加到20 mm时,吸附力由360.3 N增加到615.1 N,增加了0.71倍,与此同时,轭铁体积增加了10倍。结果表明,与其他几个参数相比,轭铁高度对吸附力的贡献率较小。
3.3 吸附单元关键参数优化设计
通过对永磁体的长度、宽度、高度以及轭铁高度、橡胶套厚度等关键参数进行分析,发现除了橡胶套厚度这一因素与吸附力呈递减关系外,其他都成递增关系。考虑到装配关系及空间限制,需要在一定的体积下,对关键参数进行优化设计,使得到的吸附力数值最优。
为了得到最优的结构参数,除了保持吸附单元体积不变外,轭铁高度设定为10 mm,只对永磁体的长、宽、高设定变量范围。然后,运用多因素设计方法,对永磁体的长度(35~60 mm)、宽度(10~40 mm)、高度(5~20 mm)进行优化分析,得到了L,W,H与吸附力F之间的三维关系,如图9所示。

图9 结构参数对吸附单元吸附力的影响
由图9可知,通过保持体积不变,对L,W,H参数优化设计,得到结构参数方案2,计算最大吸附力值为615.6 N。与方案1比较,优化后的吸附单元所提供的吸附吸附力提高了22%,优化效果显著。优化后的吸附单元的结构参数如表3所示。

表3 方案2吸附单元结构参数 mm
4 实验设计与研究
根据上述得到的结构参数,制作了2种不同结构参数的吸附单元,分别优化前和优化后的结构模型。为了证明仿真结果的合理性及测试磁吸附单元的实际吸附力,分别对2种结构进行了磁力测试实验。
实验测试设备为Instron-E10000万能材料试验机,实验过程类似于拉伸实验。在实验平台上安装1块厚度为15 mm,材料为Q235的钢板。将磁吸附单元吸附在钢板上,通过夹具将永磁单元安装在试验机的上连接法兰处,如图10所示。为了避免实验过程中出现漏磁现象,夹具与磁吸附单元均采用316不锈钢螺钉链接。
实验过程中,将上夹头匀速向上拉升,电脑终端可以测得吸附力随着位移变化而变化的实时数据。通过用Origin软件处理所得实验数据,可以得到吸附力与位移之间的关系图。然后,将测得的2组实验数据与仿真数据进行对比,如图11所示。

图10 永磁单元磁力测试实验

图11 实验数据与仿真数据关系
由图11可以看出,实验测得优化前最大吸附力为517.4 N,优化后最大吸附力为628 N,前后变化趋势相似,都呈递减趋势。通过前后对比,优化后的吸附单元吸附力提升了21.4%,与仿真值趋势基本接近,具有较好的一致性,验证了优化设计方法的合理性。其中吸附力实测值略大于仿真计算值,存在一定的偏差。主要原因可能是由于设备试验机迅速拉伸时,不能保证钢板与吸附单元平行,钢板表面出现受力不均匀。
为了进一步验证吸附单元设计的可靠性,设计了一款新型履带式爬壁机器人。机器人的尺寸参数为915 mm×979 mm×215 mm;总质量约为150 kg;负载重量大于100 kg;行走速度不大于9 m/min;越障高度不超过35 mm。如图12所示,爬壁机器人在垂直钢铁壁面进行负载越障实验,验证了吸附单元结构设计的合理性和优化方法的准确性。

图12 爬壁机器人负载越障实验
5 结束语
采用有限元方法,对永磁吸附单元进行参数化建模、磁路仿真、吸附力计算,研究了各个结构参数对吸附力的贡献关系,验证了吸附单元的工作原理,并提出了一种多因素设计的优化方法,对其结构参数进行优化设计,使其吸附力得到大幅提高。制作了新型的永磁吸附单元,通过实验测得吸附力F与距壁面距离D的关系曲线,与仿真值基本接近。将其安装在爬壁机器人样机上,成功地完成了爬壁越障试验,并确定了关键尺寸参数。
[1] 周新建, 刘祥勇. 大型油罐爬壁机器人吸附结构的优化设计[J]. 机械设计与制造, 2014(9):181-184.
[2] 郭红霞, 王雄. 重载爬壁吸附行走机构的设计与研究[J]. 控制工程, 2015, 22(2):356-359.
[3] 王兴如,衣正尧,弓永军,等.履带式船舶除锈爬壁机器人关键机构设计[J].机械设计,2009,26(12):32-34.
[4] 李凤泉. 电磁场数值计算与电磁铁设计[M]. 北京:清华大学出版社,2002.
[5] 林为干,符果行,邬琳若,等. 电磁场理论[M]. 北京:人民邮电出版社,1996.
[6] 桂仲成,陈强,孙振国,等. 爬壁机器人永磁吸附装置的优化设计[J]. 电工技术学报,2006,21(11):40-46.
[7] 张小松. 轮式悬磁吸附爬壁机器人研究[D].哈尔滨:哈尔滨工业大学,2012.
[8] 薛胜雄, 任启乐, 陈正文,等. 磁隙式爬壁机器人的研制[J]. 机械工程学报, 2011, 47(21):37-42.
[9] 汪兴潮. 船舶除锈爬壁机器人技术研究[D]. 广州:华南理工大学, 2016.

