多浮体系统在波浪作用下运动响应的数值仿真研究
,
(南京理工大学能源与动力工程学院,江苏 南京 210094)
0 引言
浮体系统在波浪循环载荷的作用下容易发生倾覆和共振,设计海上浮体时,需要对浮体的运动姿态及结构进行分析和计算。海上浮体的研究方法一般采用实验研究和理论研究,但是海洋环境极其复杂,实验研究耗时耗力,而理论研究则只能计算比较简单的物理情况,随着计算机技术的发展,数值仿真方法在海洋浮体研究当中越来越占有重要地位。Kashiwagi等[1]在二维情况下对规则形状的浮体运动进行了模拟研究。Koo[2]等对二维情况下驳船浮体在海上的运动进行了数值模拟。Hu[3],Sueyoshi[4]和Zhao[5]等对二维情况下波浪与浮体的模拟进行了研究,并且与试验数据具有很好的吻合性。Pathak[6]等应用基于三维、欧拉、流体域体积(VOF)求解器的物理模型对单个浮体与波浪耦合进行了数值分析。Shivaji[7]研究了三维情况下波浪对临近两靠泊船体的动力学响应。Gu[8]等应用VOF方法对单个浮体与波浪的耦合数值进行了分析。勾莹[9]等研究了波浪与2个相连三维浮体的相互作用,同时发现箱体运动响应的共振现象。王桂波[10]对波浪与铰接浮体系统之间的作用进行了数值仿真,并且分析了入射波方向及周期对浮体系统的影响。梁辉[11]对水下脐带缆终端安装的多浮体运动响应进行了数值模拟研究。
综上所述,应用数值仿真研究海上浮体越来越多,但是,在海上浮体的数值模拟研究还处于发展阶段,基本只能处理简单问题和简单几何物体。在此,以某海上多浮体系统为例,对海上多浮体系统在波浪作用下的数值模拟进行研究和分析,为海上浮体的研究提供一定的参考。
1 理论基础
本文的多浮体运动响应的数值模拟中,用流体域体积(VOF)多相流模型捕捉自由液面,用五阶斯托克斯波浪模型模拟波浪,以及用浮体动力学建立浮体的相互作用及多体运动模型。VOF模型是用于固定的欧拉网格上的2种或多种互不相溶流体的液面追踪技术。VOF模型是假设各种不相溶流体间在一个控制体当中满足速度、压力、温度的控制方程,可以通过控制方程描述动量、质量、能量之间的交换。求解方程的物理特性是由各相的物理性质和它们所占的体积分数决定,满足的基本方程为:
(1)

(2)
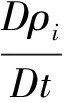
工程实际当中,除了海上浮式机场和特别细长的舰船外,一般浮体在波浪载荷下刚体位移远大于浮体的弹性位移,浮体的摇荡运动频率远远小于浮体的自振频率,所以一般研究浮体的运动学和动力学的分析当中,均将浮体视为刚体进行处理。因此,浮体动力学方程即为刚体动力学方程在海洋工程当中的应用,当静止坐标系的原点取在浮体静止无摇荡时的质心位置时,刚体动力学方程称为质心运动定理和绕质心的动量矩定理,即
(3)

(4)

(5)

(i=1,2,…,6)
(6)
j为哑标。具体公式推导可见参考文献[12]。
2 数值模型建立
2.1 问题描述
浮体模型为一复杂结构的铰接式多浮体无人平台。如图1所示为铰接浮体的几何模型示意,示意图简单描述浮体系统的几何结构。浮体系统的中心为无人中心平台,四周均布6个漂浮气囊,漂浮气囊与中心平台之间通过铰接进行连接。本文以该浮体为例,研究浮体系统在波浪作用下运动响应的数值模拟问题。
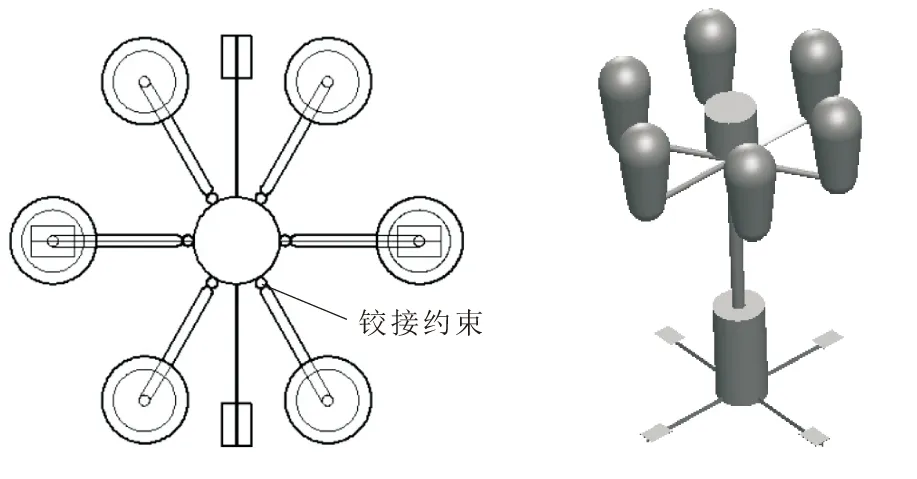
图1 浮体系统几何模型
2.2 数值模型
浮体系统在波浪的作用下不但受到入射波的作用,还受到反射波和辐射波的影响,对于复杂结构的浮体系统,浮体的运动形式是未知的。数值模拟的难点在于自由液面的捕捉,浮体在波浪作用下被动运动的仿真。对于自由液面的捕捉,采用VOF模型;对于被动运动,采用动网格技术进行解决。因此本文采用重叠网格(嵌套网格),结合浮体动力学,构建浮体系统的多体运动模型。
浮体系统结构复杂,整个波浪水池求解域大,导致网格数目多,因此需要通过体积控制,对流体域进行局部网格加密。在波浪形成区域和浮体运动区域划分较细网格,这样既能保证计算精度,提高计算的收敛性,同时也可以减少网格数量,节省计算时间。如图2所示,在波浪表面划分较细网格,用于捕捉波浪,在网格重叠区域,划分与子网格相同数量级的网格尺寸,使子网格与主网格能够很好地进行嵌套。

图2 网格划分示意
用计算流体力学对物理问题进行数值模拟,其实是对控制方程的离散求解,对控制方程求解时,需要一定的初始条件,针对相应的实际问题选择适合的物理模型后,需要进行边界条件的设置。选择物理模型,即选择控制方程。针对本文的物理问题,选择的主要的物理模型有: 三维;隐式不定常;多相相互作用;VOF(流体域体积)模型;多相状态方程;雷诺平均N-S方程;k-ε湍流模型;重力;VOF波浪模型。
因为数值模拟是在有限的计算域里面进行,所以需要对计算域进行边界条件的设置。本文数值模型一共有2个区域,一个是背景区域(即数值波浪水池),另一个为子区域(即浮体系统区域,而浮体系统区域里面的每一个物体各自为一个区域)。子区域的设置比较简单,对于浮体的各个边界均设置为物面边界(Wall),对于包裹体(子区域的重叠计算域)的外面边界设置为重叠网格边界(Overset mesh)。背景区域的设置则需要根据实验所用的波浪水池进行设置,波浪水池形状为六面体,波浪水池底部设置为墙壁(Wall),与波浪水池底部对应的另外一面设置为速度入口(Velocity Inlet)。剩下的4个周面的边界条件设置如图3所示。
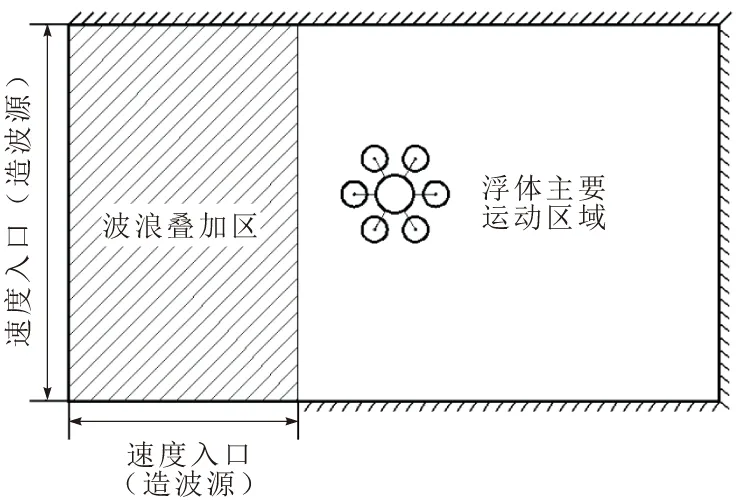
图3 数值波浪水池边界条件设置示意
由波浪水池的边界条件设置可知,波浪水池设置2个造波源(实验时,应用机械式造波机进行造波),造波后具有1个波浪叠加区域。物体放在波浪叠加区域后面,因此物体受到的入射波为迎面造的波和叠加区域来的辐射波。在数值模拟水池当中,将2个造波源设置为速度入口(Velocity Inlet),除造波源外的3个面设置为墙壁(Wall)。
本文采用VOF波浪模型,其波浪理论采用的的是Fenton的五阶斯托克斯波浪理论[13]。设置波浪的基本参数(波高、波长、水深),生成相应的体积分数、速度、压力相关的场函数。因此,对于波浪水池相应的边界条件,调用VOF波的相应的体积分数、速度和压力场函数,就可以通过场函数生成相应的波浪模型。
3 结果对比与分析
在此,主要研究多浮体系统在波浪作用下的运动响应,对于一个浮体,主要研究其6个自由度(6个模态)在波浪载荷下的变化情况。本文从多浮体系统与波浪的耦合作用,以浮体系统在波浪作用下的俯仰角(纵摇)和偏航角(艏摇)变化来研究浮体在波浪作用下的数值仿真。因此,数值模拟主要是分析和计算浮体摇荡运动的角位移最大幅值和平均变化周期。
经过数值计算后,得到浮体系统中心平台的运动响应,二级海况下的浮体系统的俯仰角和偏航角的时间历程变化曲线,如图4所示。根据时间历程曲线,浮体系统中心平台在二级海况下的俯仰角(纵摇)最大角位移达到正向为10°,负向为-9.6°。偏航角(艏摇)最大角位移正向为11.5°,负向为-12.5°。同样随着时间历程的变长,俯仰角变化趋于周期性变化,偏航角也呈现出一定规律。

图4 二级海况下浮体的俯仰角和偏航角的时间历程曲线
三级海况下浮体系统的俯仰角和偏航角的时间历程变化曲线如图5所示。根据时间历程变化曲线,浮体系统中心平台在三级海况下的俯仰角(纵摇)最大角位移达到正向为8°,负向为-12.6°。偏航角(艏摇)最大角位移正向为11.8°,负向为-7°。同样随着时间历程的变长,俯仰角变化趋于周期性变化,偏航角也呈现出一定规律。

图5 三级海况下浮体的俯仰角和偏航角的时间历程曲线
为了验证数值模型的正确性,对该浮体系统进行了二级和三级海况下浮体系统的运动情况实验。如图6所示为浮体系统运动响应的数值模拟和实验的幅值变化对比,由结果可知,数值模拟结果与实验结果具有良好的一致性,与实验结果具有很好的吻合性。

图6 数值和实验的幅值和周期结果对比
通过数值模拟结果和实验结果对比,验证数值模型的正确性和合理性,表明数值模型当中的几何结构模型、网格模型、物理模型的建立和选择是合理的。因此,可以应用该模型对本文的多浮体系统进行数值仿真研究,包括预测高海况下浮体系统的运动响应和浮体结构的设计优化。
4 结束语
基于计算流体力学方法,应用嵌套网格和多体动力学方法,解决海上浮体的被动型运动,模拟浮体系统在波浪作用下的运动,对海上浮体在不同海况下的姿态变化进行仿真和实验研究。通过仿真结果和实验结果对比分析可知,对于海上浮体的摇荡运动,采用重叠网格方法可以对其进行仿真,并且在网格的划分上也比较简单,可以推广到其他六自由度的模拟仿真中。采用的VOF方法,可以很好地捕捉波浪液面,结合波浪理论,可以很好地模拟波浪,并且接近于真实波浪。通过仿真结果与实验结果的对比表明,该方法很好地模拟浮体在海洋中的运动情况,不仅可以用于海上浮体的研究,还可以用于其他六自由度物体的仿真问题,具有一定的参考意义。
[1] Kashiwagi M, Momoda T, Inada M.A time-domain nonlinear simulation method for wave-induced motions of a floating body[ J].The Society of Naval Architects of Japan, 1998, 84: 143-152.
[2] Koo W, Kim M H, Freely floating-body simulation by a 2D fully nonlinear numerical wave tank[J].Ocean Engineering, 2004, 31(16): 2011-2046.
[3] Hu C, Kashiwagi M. Two-dimensional numerical simulation and experiment on strongly nonlinear wave-body interactions[J]. Journal of Marine Science and Technology, 2009, 14(2): 200-213.
[4] Sueyoshi M, Kashiwagi M, Naito S. Numerical simulation of wave-induced nonlinear motions of a two-dimensional floating body by the moving particle semi-implicit method[J]. Journal of Marine Science and Technology, 2008, 13(2): 85-94.
[5] Zhao X, Hu C. Numerical and experimental study on a 2-D floating body under extreme wave conditions[J]. Applied Ocean Research, 2012, 35(1): 1-13.
[6] Pathak A, Raessi M. A 3D, fully Eulerian, VOF-based solver to study the interaction between two fluids and moving rigid bodies using the fictitious domain method[J].Journal ofComputational Physics. 2016,311:87-113.
[7] Shivaji G T, Sen D. Time domain simulation of side-by-side floating bodies using a 3D numerical wave tank approach[J]. Applied Ocean Research, 2016, 58:189-217.
[8] Gu H B, Causon D M, Mingham C G, et al. Development of a free surface flow solver for the simulation of wave/body interactions[J]. European Journal of Mechanics:B/Fluids, 2013, 38(3):1-17.
[9] 勾莹, 滕斌, 宁德志. 波浪与两相连浮体的相互作用[J].中国工程科学,2004,6(7):75-80.
[10] 王桂波. 波浪与铰接多浮体系统相互作用的数值分析[D].大连:大连理工大学, 2014.
[11] 梁辉, 林影炼, 方伟,等.水下脐带缆终端安装多浮体运动响应的数值模拟[J]. 机械与电子, 2015(10):17-19.
[12] 沈庆, 陈徐钧, 江召兵. 浮体和浮式多体系统流固耦合动力分析[M]. 北京:科学出版社, 2011.
[13] Fenton, J D. A fifth-order stokes theory for steady waves[J].Journal of Waterway, Port, Coastal and Ocean Engineering, 1985,111 (2): 216-234.

