基于熔融沉积成型技术的支撑算法设计

，

(南京航空航天大学机电学院，江苏 南京 210016)

0 引言

熔融沉积成型(FDM)是快速成型技术中一项发展较为成熟的技术。熔融沉积制造技术将热塑性材料，如PLA,ABS等加热熔融，出丝机构挤出丝状熔丝，并沿着特定轨迹运动，层层堆叠而成一个完整的物体模型[1]。该技术的一个显著问题在于，由于刚喷出的熔丝呈现熔融态，它的有效堆积取决于下层是否存在实体。因此，添加支撑结构就显得尤为重要。生成的支撑结构端部和物体模型的悬空部分相融合，在模型打印结束后对支撑结构进行人为剥除。

如何合理地添加支撑结构，是确保某些模型能够完整且精确打印出来的前提条件。关于熔融沉积成型的支撑算法，已有大量的研究工作开展，其重点主要围绕待支撑部位的选择和支撑结构的添加2个方面。Allen[2]使用三角面片与水平面之间的夹角作为判断添加支撑结构的条件。Vanek等人[3]提出了模型最优的放置方式，并建立树状支撑结构。Huang[4]和Snead[5]等人利用布尔运算计算上下切片层之间的差值，以决定上层切面需要添加的支撑的面积大小。Strano[6]等人提出对支撑结构内部进行蜂窝状掏空，陈之佳[7]等人对布尔运算进行改进，提出了一种基于直线扫描的支撑结构生成方法。Wang[8]等将建筑学中的框架结构引入支撑结构设计中。魏潇然[9]等人根据熔丝的特点作为待支撑点的选取依据。陈岩[10]等人提出设置一个支撑参数来作为判断模型轮廓点是否需要添加支撑的点的判断。

在此，提出一种基于模型轮廓信息的支撑结构自动生成算法，确保模型中所有悬空部位都添加了支撑结构，能够有效地节约打印耗材和打印时间。本算法主要特点在于：以熔融态熔丝能够悬空的最大长度，作为该部分需要添加支撑结构的依据；在生成支撑结构时，根据模型自身的结构特点来调节支撑结构的长度。

1 支撑算法

本文算法的核心思想，是对实际熔融沉积过程进行一定程度上的模拟，将打印过程中的一些重要参数，运用到算法对模型的处理上来，使得搜索到的待支撑区域更符合实际情况。

对于三维打印来说，最常用的文件是STL文件，是以三角面片逼近物体真实轮廓的储存格式。但即使对于同一个模型来说，模型上不同位置的三角面片的大小也存在着较大的差异，因此对模型沿z轴分层切片，求得同一层相邻的2个轮廓点之间的距离L不一定相同。将距离L处理成与熔丝的宽度f相等，这样一来，对每个轮廓点的处理等效于处理实际打印过程中的熔丝末端位置。

1.1 寻找需要添加支撑的部位

首先要准确地找到待支撑区域，本算法中体现为找到要待支撑点集。遍历轮廓点集P{P0,…,Pi,…，Pn}(n为分层数，Pi为某一层的点集，P0为最底层)中的所有点，提取出待支撑点存入待支撑点集A中。

对于轮廓上的任一个点ta，都需要找到下一层中与自己距离最小的点tk的序号k和与之对应的最小距离值d：

(1)

d=Dta-tk

(2)

j=1,…,m；Dta-tj为点ta与下一层任一点tj的水平距离。

根据安全距离，进行待支撑点集初步选取的步骤如下：

a.从P1开始，对每层点集中的所有点进行遍历。

b.首先，判断该点ta是否为每一层起始坐标点t0，若是，则转入步骤c，若不是，则转入步骤d执行。

c.从下一层点集Pi-1起始点t0开始正向搜索，若点ta与点t1的距离值Dta-t1小于与点t0的距离值Dta-t0，依次搜索t2,t3,…，直到搜索到距离值最小的点tk；若点ta与t1点的距离值Dta-t1大于与点t0的距离值Dta-t0，则开启反向搜索模式，从点集的末尾开始，继续搜索tm,tm-1,…，直到找到距离值最小的点tk；并记录下最小距离点tk的相关信息。转入步骤e。

d.根据点ta前一点ta-1记录下的最小距离点的信息，从ta的最小距离点开始正向或者反向搜索，获得该点ta的最小距离点tk的相关信息。

e.将ta与点tk的距离值Dta-tk与熔丝伸出的安全距离Da进行比较，若大于安全距离Da，则该点为需要添加支撑的点，存入待支撑点集A中。

本算法提出了一种新的搜索方法，根据待搜索点ta前一点ta-1储存的最小距离点的信息，从前一点ta-1的最小距离点开始正向或者反向搜索。2个相邻点的最小距离点相距一般相隔很近，这样的方式能够加速搜索的进行。

而对于初步选取的待支撑点集A{a0,a1,…,ak,…,am}，由于只考虑了安全距离Da，所以点ak可能投影在下层模型的内部或者在外部，只有在外部的点才是需要添加支撑的点。将投影在下层模型内部的待支撑点，从点集A中剔除，最终留下的点集才是真正需要添加支撑的点集。

模型内部和外部的划分是由轮廓环之间的相互包含的关系来体现的。同一层可能包含多个轮廓环，轮廓环之间又可能分别存在包含的关系。在判断点ak的投影是否位于下层模型内部之前，需要首先判断哪些轮廓环包含的范围属于模型实体范围。因此，需要对轮廓环之间的关系进行一些预处理。

在此，提出了一种求解方法。由模型本身的特点可知，大的轮廓环一定不会包含在小的轮廓环内，这样就不需要求解这个关系。将所有环按大小先进行升序排序，每个环只需对排序位于之后的环求解包含关系，将有包含关系的环分别建立数个分离的拓扑数据链表。基于这些数据链表对点ak进行最终的判断。

根据待支撑点是否位于模型内部的判断条件，进行再次筛选支撑点集的步骤如下：

a. 根据点集A中的每一个点ak存储的信息，获得该点对应的下一层层号和该层的点集Pi。

b.判断ak是否与前一个ak-1在同一层，若是，转入步骤c；若否，转入步骤d执行。

c.根据前一点ak-1建立的下层轮廓环拓扑数据链表，判断该点是否位于某个数据链表中，并记录下链表中包含该投影点的环数量，根据环的数量判断该点是否位于下层模型内部。转入步骤e。

d.先对下一层的所有轮廓环按大小进行升序排列，对于每个环来说，只求解与排序位于之后的轮廓环的包含关系，将所有环分别存入对应的拓扑数据链表中，操作过程如图1和图2所示。判断该点是否位于某个数据链表中，并记录下链表中包含该投影点的环数量，根据环的数量判断该点是否位于下层模型内部。

e.从点集A中剔除位于模型内部的待支撑点，获得新的待支撑点集A。

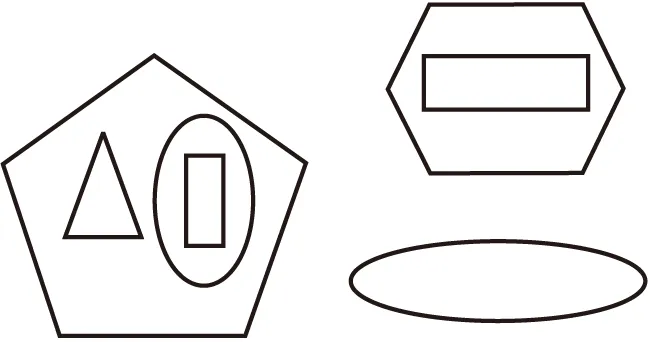
图1 同一层轮廓环之间原始的关系

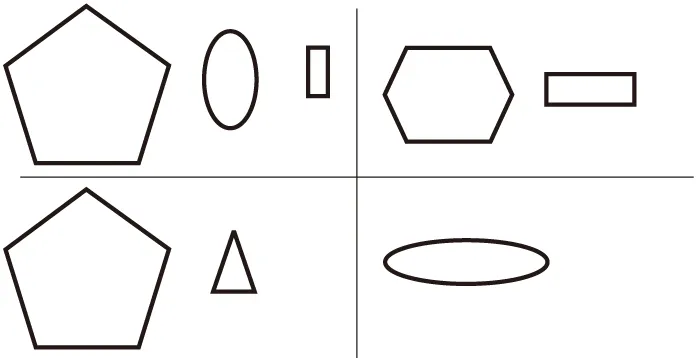
图2 步骤d处理后轮廓环之间的拓扑关系

1.2 生成支撑结构

对模型轮廓上的所有点(除了底层)都计算，并储存下一层与之对应的最小距离点的信息，这些信息的保留将极大地减少搜索时间。对于每个点ak生成的支撑柱来说，都存在实际宽度，也就说明了由点ak生成的支撑柱，不仅能够支撑点ak本身，也能将点ak周围的点一并支撑。若邻域中存在待支撑点，就不需要对这些待支撑点再次处理判断，能够有效避免支撑柱之间的实体重合。支撑柱能够稳定存在的条件为：

len≤LEN(θ) whenα=θ

(3)

len和α分别为待生成支撑柱的长度和与水平面方向的夹角，LEN(θ)为通过试验求得的能够稳定存在支撑柱的长度与角度的关系式。

寻找支撑柱两端面上中心点，即寻找支撑每个待支撑点的支撑柱上另一端的点的步骤如下：

a.遍历待支撑点集A中的所有点，若该点是第一个点a1，则转入步骤b；若不是，则转入步骤c。

b.根据点ak中储存的下层最小距离点bk1，计算出2点之间的距离len和角度α，代入支撑柱稳定存在条件，若满足，将bk1存入ak的点结构中；若不满足条件，则找到bk1的最小距离点bk2，再次进行支撑柱稳定存在条件判断，依次类推，直到找到满足条件的点bkn为止；若搜索到底层时依然没有找到符合条件的点bkn，则将ak在底层的投影点作为bkn。

c.对于其他点ak来说，首先需要向前搜索，若点ak能被前面的点ai生成的支撑柱支撑，则将ak归入ai为中心的待支撑点集中；若没有搜索到，转入步骤b。

遍历点集A中的所有点，提取出所有需要生成添加支撑的点ak以及对应的点bkn，根据这2点生成固定宽度为w的支撑柱。

支撑算法运行之后，得到了良好的支撑效果，如图3所示。

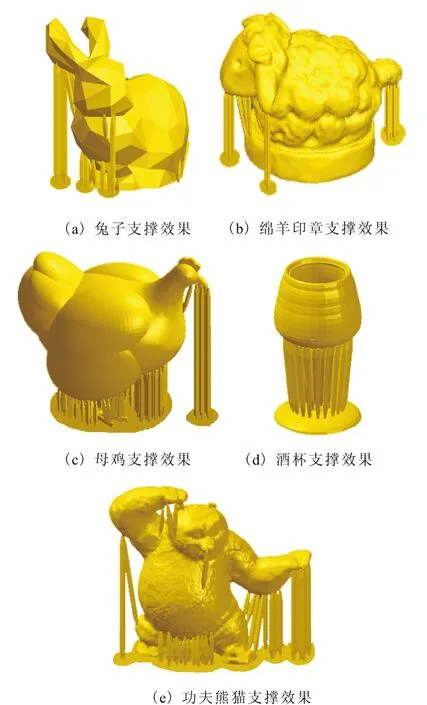
图3 生成模型的支撑效果

2 支撑参数分析

2.1 挤出丝宽度的分析试验

将相邻轮廓点之间的距离L处理成与打印过程中每条熔丝的宽度f相等，这样一来，每个点的位置更接近于实际的熔丝位置，为“寻找支撑部位”的算法部分提供了可靠的前提条件。

从喷头挤出之后，熔丝会产生一定程度的热膨胀，因此不能直接使用喷嘴宽度作为实际的熔丝宽度。一般熔融成型都是选定一组特定的工艺参数进行加工，通过试验的方式测量在不同工艺参数组合下的熔丝宽度。

试验均以聚乳酸(PLA)为原材料，室温保持25 ℃，挤出速度作为自变量，在不同温度下来测量不同挤出速度下的出丝直径。对挤出丝的宽度进行测量，采用多部位多次测量取平均值的方式。挤出丝宽度的试验数据，如图4所示。

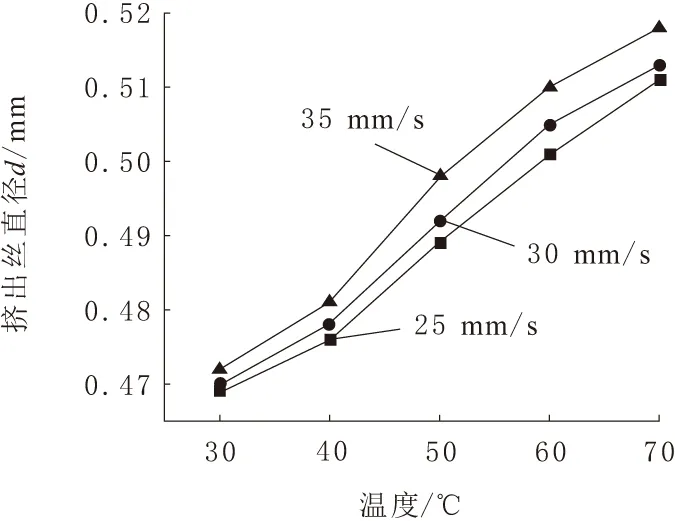
图4 温度与挤出丝宽度的关系

由图 4可以看出，随着温度升高，挤出丝直径相应增大，同样的，挤出速度对直径也有一定的影响。在接下来的试验中，选取加热温度为200 ℃，挤出速度为30 mm/s，因此选取挤出丝的宽度为0.5 mm，作为同一层相邻轮廓点之间的最大距离。

2.2 悬空距离分析试验

支撑结构的本质是对悬空距离过长的熔丝进行支撑。由于熔融状态下柔软的熔丝同样具有一定的刚度，在悬空安全距离Da内不会产生明显的塌陷，所以不需要对这些熔丝添加支撑。一般实际打印过程中每层的厚度选取范围为0.1～0.3 mm，本试验选取3个不同的分层厚度打印同一模型来进行试验。

在某一层堆积完成之后，熔丝在短时间内会冷却至固体状态。多次试验后发现，熔丝凝固后刚度足以支撑其上方未打印的其他部分，而一般喷头再次运行到该条熔丝所在位置时，熔丝已经完全凝固。因此不用考虑熔丝承受的总质量会使熔丝产生形变。所以判断某个轮廓点ta是否为待支撑点，只与该点超出下一层的轮廓线的距离有关。搜索并得到与点ta水平距离最小的下一层的轮廓点tk，求得两点之间的距离Dta-tk。若Dta-tk大于熔丝的安全悬空距离Da，则该点ta为待支撑点。表1显示了在不同分层厚度和不同悬空距离下测得的熔丝塌陷情况。

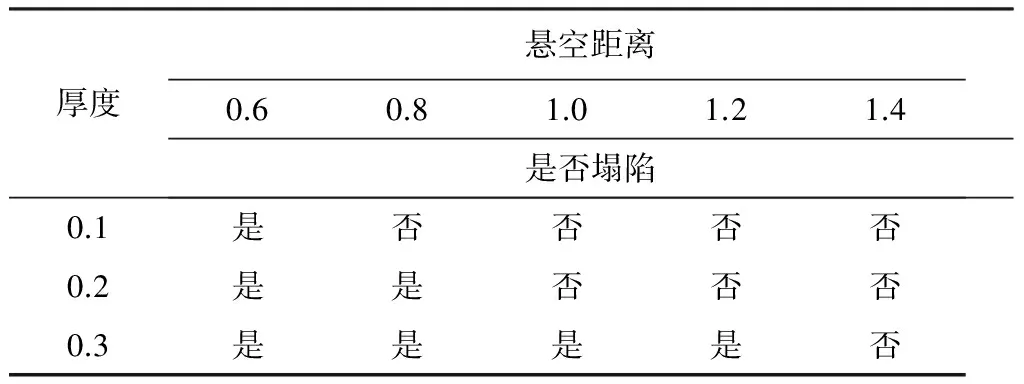
表1 不同伸出长度下熔丝的塌陷情况表 mm

根据试验结果可知，随着分层厚度的变小，熔丝的有效悬空长度变小，这是由于喷头对熔丝的挤压造成的。在接下来的试验中，统一选取0.3 mm的分层厚度，作为切片的层间距来获取模型每层的轮廓，使用1.2 mm作为熔丝的最大有效悬空长度。

2.3 支撑柱稳定存在分析试验

保证支撑效果的关键是要使支撑柱能够稳定合理地存在。通过试验得出，支撑柱可打印的最大长度以及支撑柱的偏移量与水平夹角的关系。偏移量指支撑柱顶点的实际高度和理论高度的差值。支撑柱的宽度均为1.2 mm。从图5及图6可以看出，最大可打印的长度值在60°急剧变化，偏移量在50°也有很大的变化。综合最大长度和偏移量的变化趋势，得到最大长度与角度的线性关系式，作为支撑柱稳定存在的判断依据，同时设定支撑柱与水平面的夹角不得小于50°。

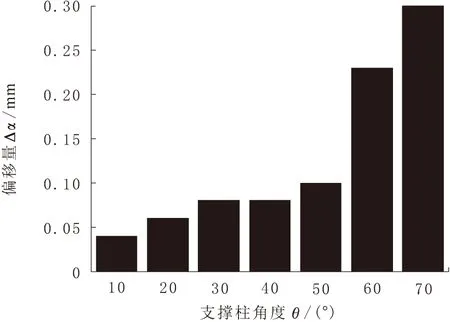
图5 偏移量与支撑柱角度的关系

图6 支撑柱角度与最大长度之间的关系

3 试验结果分析

将3个不同的模型分别应用本算法和其他2个切片引擎Slic3r，Meshmixer中的支撑算法，分析比较优劣。所有模型都是在实验室自主开发的3D打印机上完成的，以聚乳酸(PLA)为打印材料，打印速度为30 mm/s，喷头空行驶速度为60 mm/s，打印层厚为0.3 mm。

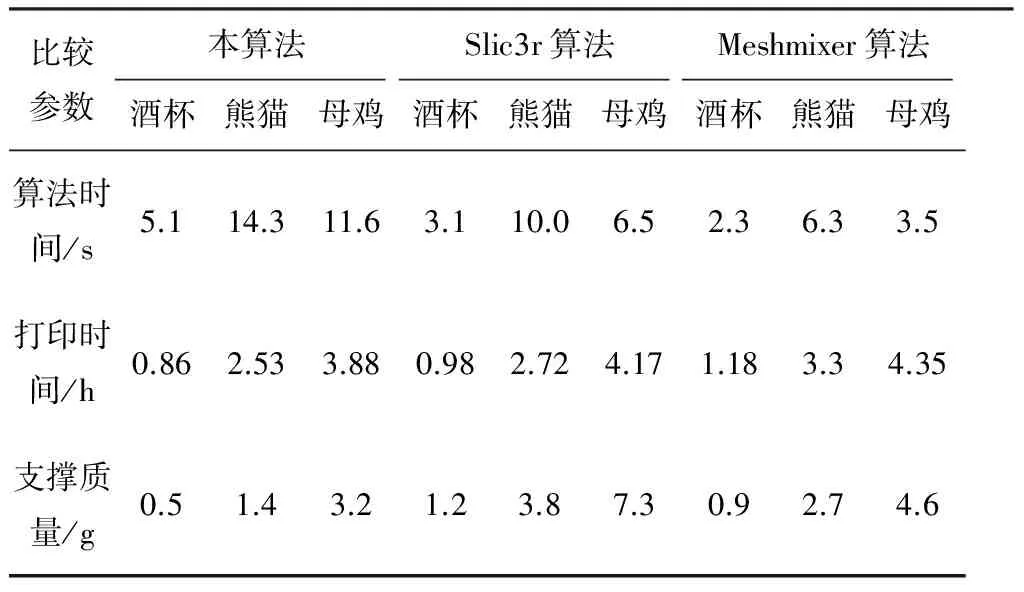
Slic3r算法通过层与层之间的布尔运算，计算出悬空区域，生成稀疏的柱状支撑结构。Meshmixer算法检测出需要添加支撑的位置，并生成树状支撑。由图7，图9和图11可知，本算法生成的结构为线性结构，生成的支撑柱的长度和角度满足图 6的关系曲线。Slic3r，Meshmixer算法都检测到的主要支撑区域，如图 7中酒杯的下沿，图 11中熊猫的手臂和鸡的喙，本算法都添加了支撑。就结构疏密而言，相比于Slic3r生成的密致结构，本算法生成的支撑显然更为稀疏，对于材料的消耗更少。图8，图10及图12展示了各个模型的打印效果。在此，主要从算法运行时间，实际打印时间，材料损耗，支撑质量4个方面来比较3个算法的优劣，试验结果如表2所示。

图7 不同算法生成的酒杯支撑效果

图8 不同算法生成的酒杯实际打印效果

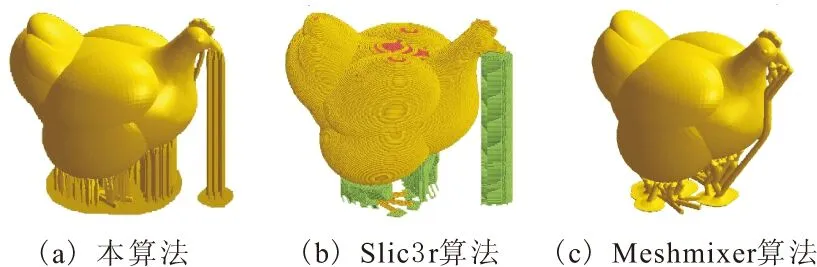
图9 不同算法生成的母鸡支撑效果

图10 不同算法生成的母鸡实际打印效果

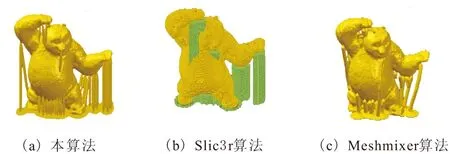
图11 不同算法生成的功夫熊猫支撑效果

图12 不同算法生成的功夫熊猫实际打印效果表2 试验数据

比较参数本算法Slic3r算法Meshmixer算法酒杯熊猫母鸡酒杯熊猫母鸡酒杯熊猫母鸡算法时间/s5．114．311．63．110．06．52．36．33．5打印时间/h0．862．533．880．982．724．171．183．34．35支撑质量/g0．51．43．21．23．87．30．92．74．6

从表2和表3可以看出，本算法在打印时间和支撑结构的耗材方面明显优于其他2种算法。但是在算法运行时间方面，对于其他2种软件算法并无优势。

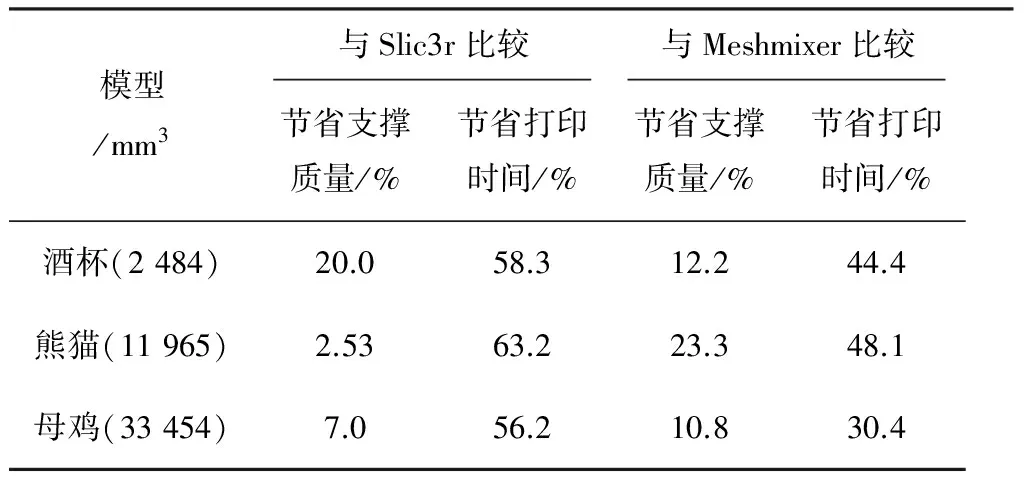
表3 本算法与Slic3r，Meshmixer的节省比较

支撑效果可以分为2个部分来进行比较，分别为材料的可剥除性和支撑区域的选择。就材料的可剥除性来看，较小的接触面积意味着在剥除时对模型的破坏更小。Slic3r算法生成的支撑结构接触面积较大，本算法和Meshmixer算法都对接触部分的支撑结构进行了削尖处理，剥除后模型能够获得更高的表面质量。就支撑区域的选择而言，由于不同算法对于添加支撑的判断条件不尽相同，其他2种算法都是以角度为阈值作为判断添加支撑的条件，而本算法是以熔丝悬空的最大长度作为判断依据，显然更为合理。从图7～图12中可以看出，本算法所判断的支撑区域大于等于Slic3r，Meshmixer算法判断的区域。

4 结束语

本文提出了熔融沉积成型制造中的一种新的支撑结构生成算法，在分析了模型的实际打印情况和熔丝特性的基础上，选取待支撑点，生成支撑柱。从实际的效果看，本算法大大节省了打印时间和打印耗材。较为准确地判断需要打印的区域，并且获得较高的模型表面质量。

本算法仍然有一些不足，主要为以下2个方面：其一，无法根据模型的实际情况自适应地变换支撑柱的粗细，以保证更好的打印和剥除效果；其二，相比于成熟的算法，本算法在运行时间上仍然有着一定的差距。

[1] 颜永年, 单忠德. 快速成形与铸造技术[M]. 北京：机械工业出版社, 2004.

[2] Allen S, Dutta D. Determination and evaluation of support structures in layered manufacturing[J]. Journal of Design & Manufacturing,1995，5: 153-162.

[3] Vanek J, Galicia J A G, Benes B. Clever support: efficient support structure generation for digital fabrication[J].Computer Graphics Forum, 2014,33(5):117-125.

[4] Huang X, Ye C, Mo J, et al.Slice data based support generation algorithm for fused deposition modeling[J].Tsinghua Science & Technology,2009,14(s1):223-228.

[5] Snead D E, Smalley D R, Cohen A L, et al. Boolean layer comparison slice: US 5854748 A[P]. 1998.

[6] Strano G, Hao L, Everson R M, et al. A new approach to the design and optimisation of support structures in additive manufacturing[J]. International Journal of Advanced Manufacturing Technology, 2013, 66(9/10/11/12):1247-1254.

[7] 陈之佳, 王丛军, 张李超. 基于直线扫描的FDM支撑自动生成算法[J]. 华中科技大学学报(自然科学版), 2004, 32(6):60-62.

[8] Wang W, Wang T Y, Yang Z, et al. Cost-effective printing of 3D objects with skin-frame structures[J]. ACM Transaction on Graphics, 2013, 32(6): 177.

[9] 魏潇然, 耿国华, 张雨禾. 熔丝沉积制造中稳固低耗支撑结构生成[J]. 自动化学报, 2016, 42(1):98-106.

[10] 陈岩, 王士玮, 杨周旺,等. FDM三维打印的支撑结构的设计算法[J]. 中国科学:信息科学, 2015, 45(2):259-269.