求解大规模稀疏有向图回路的多线程并行算法
,, ,
(山东科技大学 计算机科学与工程学院,山东 青岛 266590)
图在知识图谱、社交网络等很多领域都具有广泛应用,其中求解图的回路是一个重要问题[1]。基于DFS(deep-first search,深度优先遍历)的求解算法是目前最常用的算法[2],但随着图的规模日益增大,传统的串行求解算法由于存储能力的限制,无法求解该问题。
本文面向大规模稀疏有向图,给出了一种可在普通PC(personal computer,个人计算机)上基于多线程的并行求解算法MPCF(multithreading parallel circuit finding)。该算法首先删除图中出度为0的所有顶点,然后找到图中出度较大的顶点,采用多线程方法并行求解含有这些顶点的回路,接着删除这些顶点,再采用单线程方式求解剩余图的回路。
1 相关工作
求解图的回路是一个被广泛关注的问题,针对不同的回路,已提出了多种求解算法,如求解Hamilton回路的非递归算法[1]、求解所有顶点的最短回路的算法[3]、求解最长回路的算法[4]等。这些算法基本上都是基于DFS实现的,其核心过程是:从某个顶点出发,找出刚访问顶点的第一个未被访问的邻接点,然后再从此邻接点出发,继续找它的下一个新的邻接点进行访问,重复此步骤,直到遇到无法继续访问或者遇到一个已经被访问的顶点。如果是后者,则表示发现了一个回路。由此可见,DFS算法的主要过程就是递归搜索,而这也正是它的不足之处:当图数据集规模较小时,递归工作栈浅,内存开销小,单机运算足以胜任;但对于大规模图,单个顶点的邻接点数目众多,频繁的递归操作势必会造成内存不足,最终因堆栈溢出而出错。王玉英等[5]提出的求解有向图的全部简单回路的算法,基于矩阵运算,避免了递归调用,但对于稀疏图而言,邻接矩阵的存储方式占用了过多的存储空间,也容易造成内存溢出。
由于图结构的特殊性,顶点与顶点之间具有很强的依赖关系,很难找到一种合适的图划分方式来打破这种依赖性,而且DFS算法本身难以有效地实现并行化[6],因而目前尚无有效的基于DFS的回路求解并行算法。
近年来逐渐兴起的云计算系统为基于机群的并行图处理系统提供了有力支撑,从而催生了如Pregel[7]、GraphX[8]、GPS[9]等图处理系统。这些系统都是基于BSP(bulk synchronous parallel)模型实现的,大致处理流程如下:
1) 将图划分成多个分区,每个分区分配到集群中的多个计算节点上;
2) 将每个计算节点上的顶点均标记成“活跃”状态;
3) 开始运行一个超步,每个顶点均调用自定义的函数,函数功能包括执行计算、消息传递等;
4) 同步结束后,运行下一个超步并重复此过程,直到所有顶点都不再“活跃”并且系统中不会有任何消息在传输,这时执行过程结束。
可见,这类系统能够以批处理方式来处理大规模图数据集问题,但这些计算框架均需要搭建分布式处理系统,还要考虑分布式文件存储和任务调度,大大提高了计算成本。SC-BSP[10]模型在BSP的计算框架下引入分离器和组合器,对图划分的边集进行合理分配和管理,提高了水平扩展能力,但图划分对计算效率的影响仍然较大。此外,基于BSP模型的求解算法均是以顶点为中心的消息传递方式来处理图问题的,效率较低。
2 问题定义
G=(V,E)是一个有向图,其中V={v1,v2,…}是顶点集合,E={〈vi,vj〉|vi,vj∈V,i≠j}是有向边(又称为弧)的集合。若〈vi,vj〉∈E,则称vj为vi的邻接顶点。记
为顶点vi的出度。记
分别为所有顶点的最大出度和平均出度。定义

表示N个出度中,最大的前[Nα]个出度对应的顶点总数与G中所有顶点数量之比。记ρ0为出度为0的顶点数占顶点总数的比例,即
本文所要解决的问题是求解给定的一个大规模稀疏有向图的所有简单回路。
3 回路求解的MPCF算法
大规模稀疏图是一类非常常见的模型,如服从幂率分布的社交网络[11]。这类图具有两个非常重要的特点:一是图中存在大量出度/入度为0的顶点;二是图中仅有少部分顶点的出度/入度非常大。文献[11]的分析表明微博数据便具有上述两个特点。本文对斯坦福大学的SNAP[12]数据集中的7种不同规模的图进行了分析(表1),这些数据也满足上述两个特点。基于此,可以设想:
1) 删除出度为0的顶点,能够大幅度缩减图的规模;
2) 采用并行方式求解包含出度较大顶点的回路,删除这些顶点后,再求解剩余图的回路,可有效提高计算效率。

表1 有向稀疏图出度的分析
MPCF算法便是基于上述思想设计的。在初始化相关变量(第1行)、对顶点出度排序(第2、3行)后,从图中删除出度为0的顶点(第4行),并根据参数α将出度排序靠前的顶点放入集合Vlarge中(第5行)。第6、7行启动n个线程,其中nmax是预先指定的最大线程数。第8~11行为并行执行过程,每个线程求包含Vlarge中一个顶点的回路集合,同时为保证不同线程求解的是不同顶点,将算法第9行中nextVertex()方法做加锁处理。第12行将Vlarge中的顶点删除,接着求出剩余顶点的导出子图G′(第13行)。第14~16行以串行方式求G′的回路集合。此处之所以使用串行,是因为图G′顶点数目庞大,但由于没有大出度顶点,边数目减少,图变得极其稀疏,在图规模一定的情况下,使用串行算法即可在较快时间内求解,并行算法由于线程启动、管理等方面的时间消耗,反而需要花费更多的时间。该算法中,nextVertex()用于返回Vlarge中下一个尚未求解其回路的顶点;findCircuits(v)用于求包含顶点v的回路集合,即以顶点v作为起点和终点的回路的集合;induceSubGraph(V′)用于求顶点集合V′的导出子图。
需要指出的是:该算法是在单机上执行多线程的,各个线程共享内存,而且线程在求回路时,对图G是只读操作,因此图G不需要分割存储,即各线程无需存储G的信息。

MPCF算法Input:DirectedgraphG=(V,E),parameterαOutput:AllcircuitssetCSofGprocedureMPCF(G,α)1.CS←Φ2.Getdoutiforeachvi∈VusingEquation(1)3.Sortdoutiinnon⁃descendingordera1,a2,…,aN{}4.V′←V-vi|douti=0{}5.Vlarge←vi|a[Nα]£douti£a1{}6.n←minVlarge,nmax{}7.Forknthreads8.foreachthreaddoinparallel9. synchronizedu←nextVertex()10. CS←CS∪findCircuits(u)11.endfor12.V′←V′-Vlarge13.G′←induceSubGraph(V′)14.forallv∈V′do15. CS←CS∪findCircuits(v)16.endfor17.returnCS18.endprocedure
假定使用邻接表来存储图数据,那么算法的时间复杂性分析如下。第2行需O(|V|+|E|)来求各个顶点的出度。第3行排序需用O(NlogN)来排序N个不同的出度值。第4行需要O(ρ0|V|)来删除出度为0的顶点。第8~11行并行过程的时间取决于求解包含出度最大顶点u的回路的时间。在最坏情况下,若以u为根的生成树包含了V′的所有顶点,使用DFS思想求回路的方法需要时间为O((1-ρ0)|V|+|E|)。考虑到图的稀疏性,第12~13行所求出的导出子图仅包含非常少的边,所以第14~16行的时间不会超过O((1-ρ0)|V|)。因此,该算法的时间复杂性为O(2|V|+2|E|+NlogN)。对于稀疏图,N<|E|≪|V|2,所以MPCF算法的时间复杂度要低于文献[5]所提出算法的时间复杂度O(|V|2)。
4 实验与结果分析
本文进行实验的图数据即表1所示的7个有向图。实验用计算机的CPU为Intel® CoreTMi5-3210M CPU @ 2.50 GHz,运行内存为6 GB,操作系统为Windows10(64位)。算法采用JAVA语言实现,设置JVM(JAVA虚拟机)最大堆内存参数“-Xmx”为4 GB。每个单独实验均做10次,每次实验完成后,重启主机以保证每次实验环境一致,并且互不影响。运行时间取10次平均值。
4.1 α的取值
α是MPCF算法的关键参数,决定了进入并行环节的顶点数量,因此首先需要根据图的规模来选取α值。此处分别对α取0.1、0.2和0.3进行实验,结果如表2所示,表中tpara和tseq分别表示算法1中第8~11步并行求解的时间、第14~16步串行求解的时间,ttotal=tpara+tseq。“—”表示串行部分内存溢出,无法求出所有的回路。

表2 不同α值实验结果
根据实验结果,可以得出:
1) 当顶点数在10万以下时,α=0.1所需计算时间最少。
2) 当顶点数在10万到100万之间时,α=0.1已无法串行求解G′的回路。α=0.2时所需时间最少。
3) 当顶点数超过100万时,只有α=0.3方可求解回路。
4.2 MPCF算法性能分析
由于文献[5]的算法是基于矩阵乘法运算的,对于表1中的大规模图,仅图的邻接矩阵便需要占用大量的内存空间。如对于10万个顶点的图,即使每个矩阵元素仅需1 B内存,整个邻接矩阵就需要占用超过9 GB内存,在计算过程中,则至少需要20 GB内存。因此该算法无法在普通PC上实现。
本文将MPCF算法与基于DFS的串行回路求解算法进行对比分析,执行时间如表3所示,占用内存情况如图1所示。表3中tdfs为串行求解算法所需的时间。tpara和tseq是在4.1节中确定的α值基础上求解算法的时间。
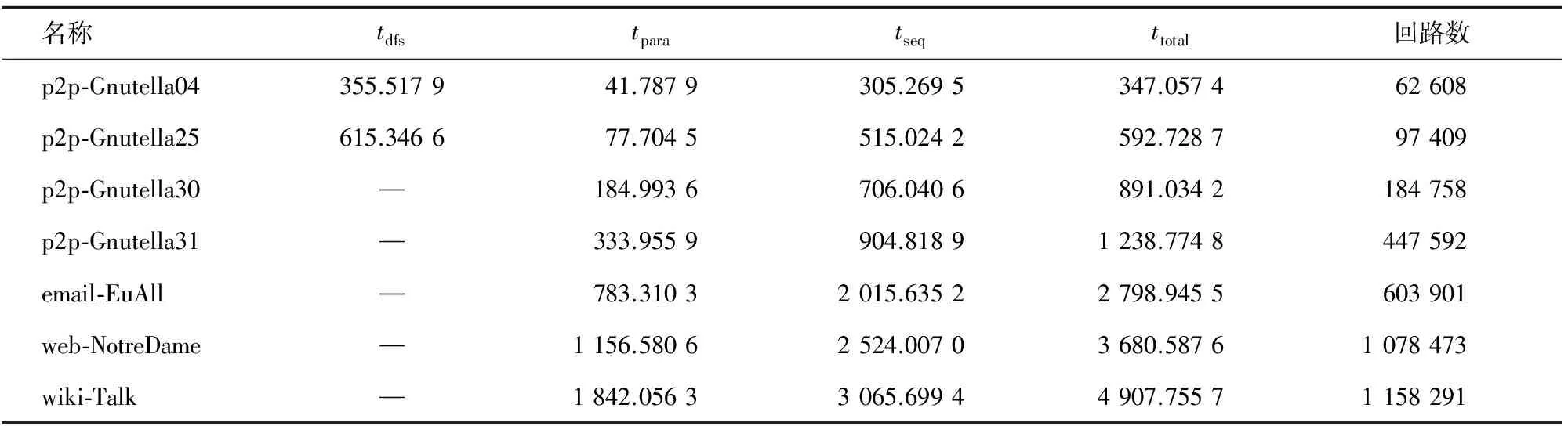
表3 算法性能分析
可以看出,p2p-Gnutella04和p2p-Gnutella25两个图的数据规模较小,串行算法占用内存在4 GB以下,且能在数百毫秒内求出所有的有向回路(少于10万个)。MPCF算法的执行时间仅略少于串行算法,约为串行算法时间的96%~97%,tpara占全部执行时间的12%~13%。从内存情况看,这两个图的串行求解算法没有因为递归而导致内存溢出,MPCF算法的并行部分和串行部分占用内存为串行算法的30%~65%。
对于其余的4个图,它们包含的有向回路数在18万条以上,此时串行求解算法的递归部分占用内存急剧增加,超过了3.9 GB,Java程序出现内存溢出(Out of Memory)异常,从而无法求出所有的有向回路。MPCF算法的并行阶段仅求解极少量顶点的回路,串行阶段因处理的图G′已非常稀疏而递归层次浅,所以MPCF算法的内存开销未溢出。但随着图中所包含回路数量的增加,MPCF算法所需的时间和内存也在增长。从时间上来看,MPCF算法的并行部分约为串行部分时间的20%~37%;从内存上来看,MPCF算法的并行部分约为串行部分时间的78%~94%。
因此,MPCF算法在内存方面能够保证大规模图有向回路的正常求解。

图1 算法内存分析
5 总结
针对传统基于DFS思想的算法无法在普通PC上求解大规模稀疏图所有有向回路的问题,通过对图数据集的分析,提出了一种基于多线程的并行求解算法。同时,为了测试此种求解方式的可行性,本文使用真实社交网络数据进行实验,结果表明此算法可在普通PC上求得大规模有向稀疏图的所有回路。本文所提出的算法同样适用于无向图。下一步,我们将进一步研究在多核、众核处理器上处理更大规模图的算法。
[1]SILVA J L C,ROCHA L,SILVA B C H.A new algorithm for finding all tours and Hamiltonian circuits in graphs[J].IEEE Latin America Transactions,2016,14(2):831-836.
[2]LI B,XIONG L,YIN J.Large degree vertices in longest cycles of graphs,I[J].Discussiones Mathematicae Graph Theory,2016,36(2):363-382.
[3]YUSTER R.A shortest cycle for each vertex of a graph[J].Information Processing Letters,2011,111(21-22):1057-1061.
[4]PAULUSMA D,YOSHIMOTO K.Cycles through specified vertices in triangle-free graphs[J].Discussiones Mathematicae Graph Theory,2007,27(1):179-191.
[5]王玉英,陈平,苏旸.生成有向图中全部简单回路的一种新算法[J].山西师范大学学报(自然科学版),2008,36(4):12-15.
WANG Yuying,CHEN Ping,SU Yang.A new algorithm to find all elementary circuits of a directed graph[J].Journal of Shaanxi Normal University(Natural Science),2008,36(4):12-15.
[6]REIF J H.Depth-first search is inherently sequential[J].Information Processing Letters,1985,20(5):229-234.
[7]MALEWICZ G,AUSTERN M H,BIK A J C,et al.Pregel:A system for large-scale graph processing[C]//ACM SIGMOD International Conference on Management of Data,2010:135-146.
[8]GONZALEZ J E,XIN R S,DAVE A,et al.GraphX:Graph processing in a distributed dataflow framework[C]//Proceedings of 11th USENIX Symposium on Operating Systems Design and Implementation (OSDI 14),2014:599-613.
[9]SALIHOGLU S,WIDOM J.GPS:A graph processing system[C]//Proceedings of 25th International Conference on Scientific and Statistical Database Management.Baltimore,Maryland,USA,July 2013:Article No.22.
[10]赵翔,李博,商海川,等.一种改进的基于BSP的大图计算模型[J].计算机学报,2017,40(1):223-235.
ZHAO Xiang,LI Bo,SHANG Haichuan,et al.A revised BSP-based massive graph computation model[J].Chinese Journal of Computers,2017,40(1):223-235.
[11]罗由平,周召敏,李丽娟,等.基于幂率分布的社交网络规律分析[J].计算机工程,2015,41(7):299-304.
LUO Youping,ZHOU Zhaomin,LI Lijuan,et al.Social network discipline analysis based on power-law distribution[J].Computer Engineering,2015,41(7):299-304.
[12]LESKOVEC J,KREVL A.SNAP datasets:Stanford large network dataset collection[DB/OL].(2017-07-24)http://snap.stanford.edu/data,2014.

