基于毫小薄片漏斗试样的材料弹塑性循环应力应变关系测试方法研究

尹 涛，蔡力勋，陈 辉，姚 迪

（西南交通大学力学与工程学院 应用力学与结构安全四川省重点实验室，四川 成都 610031）

0 引 言

毫小尺寸试样测试在服役结构和小尺寸构件的材料性能备受关注。发展以微损取样代替常规的破坏性取样来测试材料力学性能的毫小尺寸试样试验方法，对评价服役设备的性能、结构安全性和剩余寿命有重要意义。毫小尺寸试样的疲劳测试性能可以广泛应用于航空航天、轮船、汽车、微机械、微电子和生物修复等领域的关键构件安全评价，可以克服材料尺寸与试样数量的传统限制，具有重要的学术价值和工程应用前景。在宏观尺度下，相较于大尺寸试样，国内外较少开展小尺寸薄片试样的低周疲劳性能研究。

材料的低循环应力-应变关系和低周疲劳Manson-Coffin律用于广大弹性区约束下结构局部塑性区的疲劳寿命分析。材料的轴向等幅低循环应力-应变关系通常采用等直圆棒试样按GB/T 15248——2008《金属材料轴向等幅低循环疲劳试验方法》[1]和ISO 12106——2003Metallic materials-fatigue testing-axial strain-controlled method[2]推荐的多试样法或单试样法进行试验获得。针对厚度大于2.5mm的薄板材料，现行试验标准给出了等直片状试样和不产生应力集中的大曲率半径漏斗试样来获取等幅低循环应力-应变关系，而厚度小于2.5 mm（如1 mm左右）的薄片材料难以采用现行标准推荐的疲劳试样进行测试。针对厚度小于2.5 mm的薄板材料，He等[3]采用2mm的等直段片状试样完成拉-拉非等幅疲劳试验从而进行疲劳性能分析，故无法借鉴其用以等幅低循环应力-应变关系的获取。

毫小薄片疲劳试样可定义为平面构形尺寸和塑性区尺寸在毫米级范围且厚度小于2.5mm的试样。为了避免薄片试样在等幅低周疲劳试验中发生失稳，薄片试样可设计为漏斗型。近20年来，国内外学者利用薄片漏斗试样进行了材料疲劳性能测试方法的探索，如Ye等[4]采用薄片漏斗试样研究了钛合金TC4局部塑性应变和多尺度的疲劳裂纹扩展行为之间的相互作用。但是针对厚度小于2.5mm的金属板材低循环应力-应变关系研究仍罕见报道。Wisner等[5]采用小漏斗半径的薄片漏斗缺口试样实现了锆合金板材的常温低循环试验，试验采用径向应变控制，并以漏斗根部的等效塑性应变幅与平均弹性应变幅之和作为轴向应变幅，以及以漏斗根部横截面的平均应力作为轴向应力幅，进而完成对锆合金板材的疲劳寿命预估。早期的这项研究因存在应力与应变集中问题，其结果与漏斗根部材料单元的真实情况存在较大偏差。为了实现1mm和2mm厚的板材或焊缝的疲劳特性研究，蔡力勋等[6-10]也采用类似的薄片漏斗试样开展研究，利用径向引伸计实现低循环试验应变控制，然后通过等效方法将径向应变换算为轴向应变，进而获取材料低循环性能，所采用的等效方法仍具有较大近似性。黄学伟等[11-13]提出了改进的薄片漏斗试样，并根据有限元分析建立轴向控制应变同漏斗根部轴向应变的转换关系，由于薄片难以获得真实的循环应力-应变关系，在有限元分析只好采用单调拉伸的应力-应变关系作为输入材料属性，未考虑材料循环强化。贾琦等[14-15]同样采用薄片漏斗试样进行了多种材料的低循环试验，并提出针对具有循环Masing效应材料的等直圆棒试样的低循环试验结果，取平移后最大应变幅稳定阶段应力-应变滞回环上升段作为材料的循环应力-应变关系，文章未提出如何通过薄片漏斗试样来获取材料的循环应力-应变关系。薄片试样的低周疲劳因材料循环应力-应变关系难以获取而在材料测试领域一直是亟待解决的困难问题。

Chen等[16]发展了一套基于测试载荷-位移曲线预测材料单轴应力-应变关系的压痕理论模型（equivalent-energy indentation model，EIM），该模型采用能量分离方法有效建立了Hollomon应力-应变关系参量（E、σy和n）与P和h的半解析方程，为材料的应力-应变关系理论求解提供了可能。本文将借鉴EIM模型的能量理论提出采用毫小薄片漏斗试样获取材料循环应力-应变关系的新测试方法。通过合理设计试样、二次夹具和试验方案，开展了毫小尺寸薄片漏斗试样、小尺寸薄片漏斗试样和等直圆棒试样的变幅对称应变控制低循环试验；采用能量分离函数，结合毫小薄片漏斗试样的循环稳定载荷幅-位移幅关系提出了具有尺寸与材料普适的薄片漏斗试样的循环应力-应变关系模型。

1 研究条件

1.1 材料、试样及加载装置设计

考虑到薄片试样的小尺寸化和对称应变疲劳试样的拉压受力特点，设计了图1所示的毫小尺寸薄片漏斗试样（MSN型试样）、小尺寸薄片漏斗试样（SSN型试样）和等直圆棒试样（SRB型试样），分别用于间接和直接获取材料的循环应力-应变关系，其中，SSN型试样扣除夹持段部分仍可理解为毫小尺寸试样。对薄板材料，等宽度试样在弹塑性应变幅情况下容易失稳，而采用圆弧漏斗试样，由于其圆弧根部材料单元具有单轴变形特性且能产生较大应力集中，可避免试样循环失稳。

由于MSN型试样尺寸限制，需充分考虑试样安装的稳固性和对中性，以保证试样拉压疲劳过程中不会出现松动和翘曲。MSN型试样可通过数控电火花精密加工，图2（a）中的限位槽使得试样与夹具之间在循环载荷下不会出现相对位移。图2中夹持板与试验机夹头连接，对中平台用于该型夹具与试验机夹头的限位安装从而避免试样轴向偏心，盖板与夹具由螺纹杆连接，用于纵向固定试样，防止试样被挤出限位槽，同时增加夹具对试样表面的夹持力。

表1 试样几何尺寸

图1 试样尺寸构形

图2 夹具示意

表2 316L不锈钢主要化学成分的质量百分数 %

图3 316L不锈钢试样照片

表3 316L不锈钢的拉伸力学性能

表1给出了MSN型和SSN型试样的尺寸。图1所示MSN型试样与SSN型试样区别为夹持方式不同，它们在跨漏斗两侧引伸计标距内的工作段是自相似的，因此SSN型试样虽然尺寸大于MSN型试样，但其工作段仍可代表毫小级别试样的受力和变形特征。图2所示夹具采用文献[6，15]推荐的方法来实现SSN型试样的稳固对中夹持。

试样材料采用316 L不锈钢，其化学成分和机械性能分别如表 2、表 3 所示。采用图 3（a）、图 3（b）所示的尺寸薄片漏斗试样完成应变对称的变幅低循环试验。图4给出了SRB型试样、MSN型试样、SSN型试样的试验情况。

1.2 试验设备和加载方法

MSN型试样的试验设备为Care IBTC-300原位双向拉压疲劳试验机 （载荷量程1 kN），控制器为Multi-Channel Test Controller，驱动器为Multi-Channel Test Driver，控制软件为Care-Test-Fatigue。SSN型试样和SRB型试样的试验设备为美国MTS 809（25kN）电液伺服材料试验机，控制系统为TestStar II，应用软件为MTS790.10/SX。两台试验机载荷传感器准确度均为0.5级，均通过计算机对试验过程进行闭环控制和实时数据采集。

图4 316L不锈钢3类试样的疲劳试验照片

为实现低循环试验的轴向应变控制，MSN型试样和SRB型试样采用MTS 632.29F-30引伸计（标距为5mm，测量范围-10%～30%），SSN型试样采用MTS 632.54F-14引伸计（标距为12 mm，测量范围-10%～20%）。两种引伸计准确度均为0.5级。

本文所有试验均采用应变对称的变幅循环试验方法，每种构形试样各取两个试样进行试验，控制应变幅自低到高，每级应变幅下分别循环200周，三角波加载，MSN 型试样的加载速率为 0.002mm/（mm·s），SSN和SRB型试样的加载速率为0.008mm/（mm·s）。

1.3 有限元分析

根据MSN型和SSN型试样的载荷-跨漏斗两侧位移试验曲线（P-h曲线），为获取薄片漏斗试样的循环应力-应变关系，可采用有限元方法模拟试样跨漏斗两侧引伸计标距内工作段的受力与变形。针对两类薄片漏斗试样，均可建立如图5所示的薄片漏斗试样三维和平面模型进行分析，三维模型采用Solid186六面体单元进行网格划分，考虑结果精度，对漏斗根部进行网格加密，平面模型采用Plane183带厚度的平面应力单元进行网格划分。

有限元计算采用位移加载控制，边界条件如图5所示，提取试样跨漏斗根部两侧各h/2处两节点的相对位移与下端所有节点的总载荷作为计算结果输出，从而实现毫小薄片漏斗试样试验的数值模拟。为了确保有限元计算提取的载荷结果能正确反映真实试验结果，建议有限元模型高度H等于毫小薄片漏斗试样的总高度。

图5 毫小薄片漏斗试样有限元网格模型

图6 三维模型和平面应力模型有限元计算结果比较

考虑到MSN型试样漏斗根部厚度不同，或许会产生非平面应力状态，因此针对R=2 mm、W=6 mm、H=24 mm，厚度t为 0.5，0.8，1 mm的毫小薄片漏斗试样模型，分别进行平面应力和三维条件下不同厚度的弹塑性模拟计算，计算的P-h曲线结果如图6所示。可见，平面应力模型和不同厚度（分别为0.5，0.8，1mm）的三维模型计算得到的线载荷-位移（PL-h）曲线基本重合，其中PL=P·t-1，位移h等于轴向控制应变与引伸计标距段的乘积。说明针对厚度小于1mm的MSN型试样可采用平面应力2D模型代替3D模型进行P-h曲线的准确获取。由于自相似性，几何比λ=3的SSN形试样在厚度小于2.4 mm时也可采用平面应力2D模型代替3D模型准确获取P-h曲线。给出3D模型（t=1 mm）漏斗根部沿厚度方向节点的εeq和σeq分布，如图7和图8所示。沿厚度方向节点的εeq和σeq较平均值相差不超过1%。

图7 3D模型漏斗根部沿厚度方向节点等效应变分布

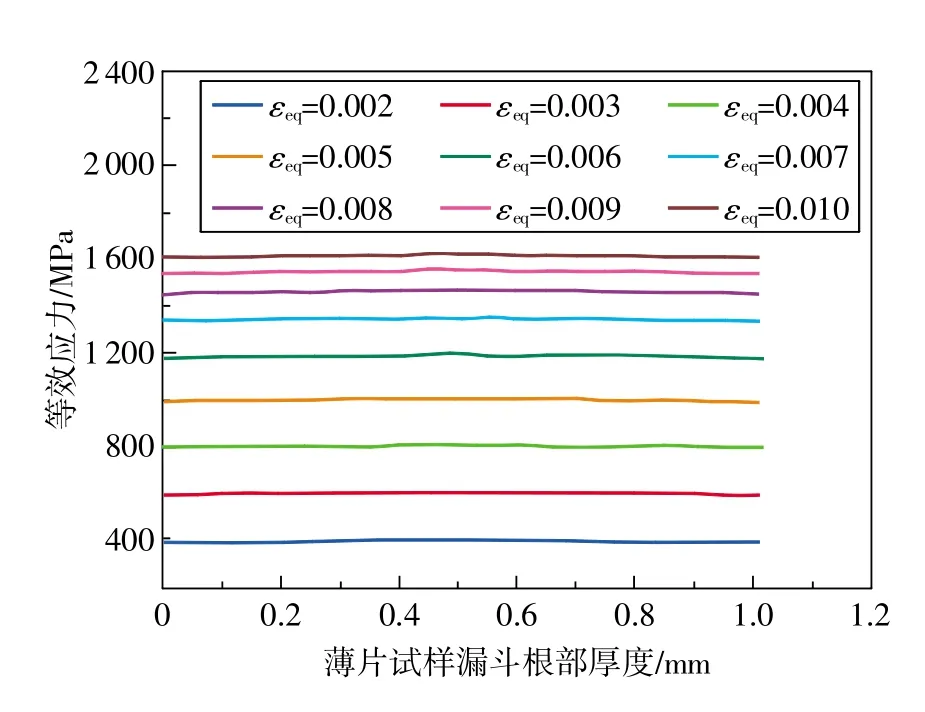
图8 3D模型漏斗根部沿厚度方向节点等效应力分布

同一加载位移下，漏斗根部节点εeq相同时，将平面应力2D模型漏斗根部节点的等效应力（σeq）与3D模型漏斗根部沿厚度方向等效应力的平均值进行比较如图9所示，可见两者相差不超过1.2%。

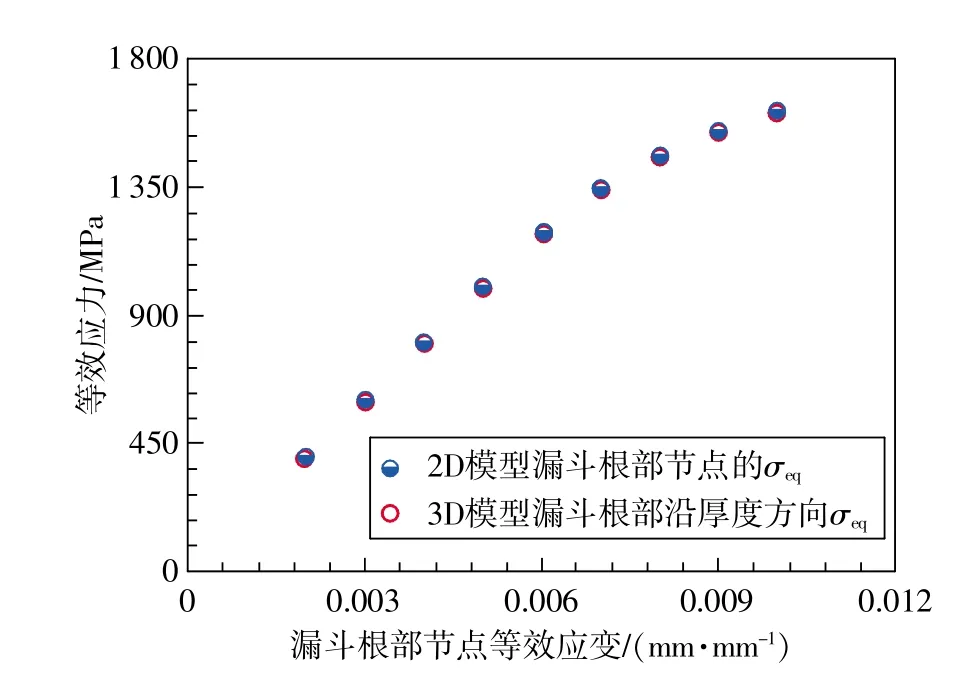
图9 漏斗根部节点等效应变相同时平面应力2D模型和3D模型σeq计算结果

因此，可采用平面应力2D模型实现薄板试样漏斗根部等效应力和等效应变的精确计算。

图10给出了毫小薄片漏斗试样有限元模型漏斗根部节点在加载过程中3向主应力的变化规律。可见，第2主应力和第3主应力等于零（σ2=σ3=0），第1主应力（σ1）随载荷的增加而增加，可知在应变范围[0，0.7]内，漏斗根部处于单轴应力状态。由式（1）可知，该点的Mises等效应力σeq等于第1主应力σ1（σeq=σ1）。

图10 漏斗根部三向应力状态

2 循环应力-应变关系模型

2.1 基于能量法建立循环应力-应变关系模型

毫小薄片漏斗低循环试验中，材料局部塑性与含裂纹构件的小范围屈服大致相当，故选用对屈服区描述较好的Ramberg-Osgood（R-O）应力-应变关系模型[17]：

式中：ε、εe、εp——总应变、弹性应变、塑性应变；

σ——总应力；

E——弹性模量；

K——应力强化系数；

n——应力硬化指数。

对于符合Ramberg-Osgood模型的材料，其变形可参考应变的方式分解为弹性变形和塑性变形两个部分的叠加：

式中：he——弹性位移；

hp——塑性位移。

假设材料发生弹性变形所产生的弹性应变能Ue满足如下能量分离函数：

式中：f1（E）——材料函数；

f2（ξ）——几何变形域函数；

f3（he）——变形函数；

α0——弹性等效变形体积系数；

ξ——变形域的特征体积；

h′——等效位移。

考虑到ξ=A′h′，A′为有效特征面积。 由功能原理和卡氏定理，可得：

若材料发生塑性变形所耗散的塑性应变能Up也满足能量分离，则也可假定能量分离函数如下：

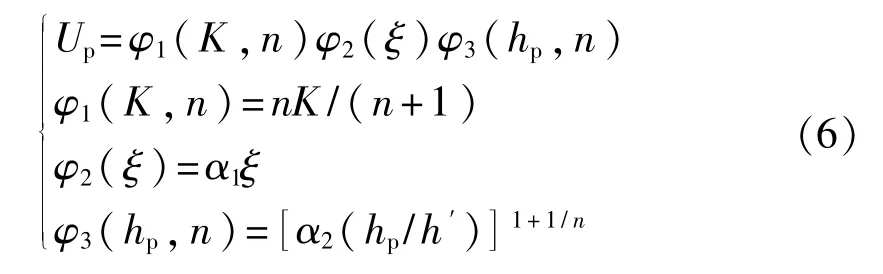
式中：φ1（K，n）——材料函数；

φ2（ξ）——几何变形域函数；

φ3（hp，n）——变形函数；

α1——塑性等效变形体积系数；

α2——等效应变系数。

由功能原理和卡氏定理得：

为便于归一化表达，令尺寸比λ=W/R。假设毫小薄片漏斗试样的变形域Ω高度为L，如图11所示，高度为L的模型体积完全包含整个变形域Ω范围。假定变形域的特征体积ξ与图11所示的模型体积ξ模型之比为ρ，即：

图11 薄片漏斗试样低周疲劳试验的变形域Ω

ξ经过有限元标定得出，当L=5W/6，ρ=R/（L-2R）时，能使得不同尺寸的几何构形试样的P*-h*曲线均重合良好。图12给出了同一弹塑性应力-应变关系、不同λ的几何构形P*-h*曲线有限元结果。此时：

图12 不同几何构形的P*-h*曲线

结合式（3）、式（5）、式（7）和式（9）可以得到：

通过给定弹性模量E=195GPa，泊松比ν=0.3，针对λ分别为 3.0，3.5，4.0，4.5，5.0 的 5 种 MSN 型试样各进行一次纯弹性计算标定出弹性等效变形体积系数α0，如表4所示。

通常符合Ramberg-Osgood应力-应变关系模型的金属，其应变强化系数K取为100～3000MPa，应变硬化指数的倒数1/n取为0.1～0.5。因此针对λ分别为 3.0，3.5，4.0，4.5，5.0 的 5 种毫小薄片漏斗试样几何构形、18 种不同材料 （K=100，1000，3000MPa，1/n=0.1，0.125，0.2，0.3，0.4，0.5）进行弹塑性有限元计算标定出塑性等效变形体积系数α1、等效应变系数α2，如表 4 所示。

表4 循环应力-应变关系模型参量

如图13所示，循环应力-应变关系模型参量随λ的变化规律满足：

其中，a0～a4、b0～b4、c0～c4为常数系数，如表 5 所示。 当毫小薄片漏斗试样的λ位于 3～5 时，α0、α1、α2可通过插值得到。

2.2 循环应力-应变关系模型的有限元验证

2.2.1 正向预测

图13 循环应力-应变关系模型参量随λ的变化规律

表5 式（10）中参数

图14 P-h曲线的有限元计算和模型预测结果

基于已经建立的循环应力-应变关系预测方程，根据式（5）、式（7）、式（9）对不同已知幂律硬化材料的载荷-位移曲线进行预测。针对λ=3～5的薄片漏斗试样进行了大量有限元计算验证，验证材料的应变强化系数K=100～3000MPa，应变强化系数的倒数1/n=0.1～0.5，模型材料的范围基本涵盖大部分金属材料。图14给出了5种情况下有限元计算的P-h曲线（FEA）和模型方程预测的结果，可见，P-h曲线的公式预测结果与有限元计算结果吻合良好。事实上，共15种不同λ和K组合下，6种应变硬化指数材料（共80种材料）的有限元计算和公式预测结果均吻合。

图15 循环应力应变曲线的模型预测和有限元输入曲线对比

2.2.2 反向预测

取对弹塑性幂律材料，通过线性P=ηhe拟合λ=3～5的毫小薄片漏斗试样循环稳定阶段的P-he曲线，就可以由式（12）得到该材料的弹性模量E，由hp=h-he得到P-hp曲线，对P-hp曲线进行幂率P=βhpγ拟合。由于γ与n呈线性关系，β与K呈线性关系，可由式（12）得到该材料的塑性参量K、n。

其中η、β、γ为拟合系数。

针对λ=3～5的薄片漏斗试样进行了大量有限元计算验证，验证材料的应变强化系数K=100～3000MPa，应变强化系数的倒数1/n=0.1～0.5，有限元计算得到的P-hp曲线，由式（12）预测循环应力-应变关系如图15所示。

由图15可知，通过循环应力-应变关系模型反向预测的循环应力-应变关系和输入有限元的初始应力-应变关系吻合良好。

3 316L不锈钢低循环试验及结果比较

完成SRB型试样的应变对称变幅低循环试验，得到循环稳定轴向应力-轴向应变滞回曲线。经对称化处理后如图16所示。根据GB/T 15248——2008获得316 L不锈钢的循环应力-应变关系（εc-σc）如图17所示。

针对MSN型和SSN型两类共6种尺寸的薄片漏斗试样完成应变对称变幅低循环试验，其中MSN型试样的控制位移幅为0.003～0.025 mm；5种尺寸SSN型试样的控制应变幅为0.0005～0.005mm·mm-1。得到循环稳定的线载荷-位移（PL-h）滞回曲线，经过对称化（使PL和h沿坐标轴对称)处理后如图18所示。图中仅示出了MSN型和λ=3的SSN型薄片漏斗试样的PL-h曲线。连接各级滞回曲线的顶点获得316L不锈钢低循环稳定的线载荷-位移（PLc-hc）曲线作为循环应力-应变关系在不同几何构形下的表征，如图19所示。

图16 循环稳定轴向σ-ε滞回曲线

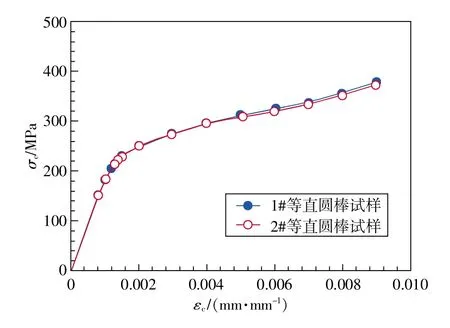
图17 316L不锈钢的循环应力-应变关系

图18 循环稳定阶段MSN型试样和SSN型试样实验的PL-h曲线

图19 6种构形薄片漏斗试样PLc-hc曲线

将6种构形薄片漏斗试样循环稳定阶段的线载荷-位移（PLc-hc）曲线用式（12）可以得到 316 L 不锈钢的循环应力-应变关系。与SRB型试样得到的循环应力-应变关系比较，如图20所示，可以看出预测曲线与试验曲线在较小分散带内。

图21给出了采用循环应力-应变关系模型方程基于MSN试样和不同λ值SSN试样（各两个）预测316L不锈钢循环应力-应变关系的相对误差图。同一循环应变幅下，循环应力的相对误差δ表明循环应力-应变关系模型方程预测的精度，δ越小表示预测越精准。δ的计算公式为

图20 6种构形薄片漏斗试样循环应力-应变关系预测结果及对比

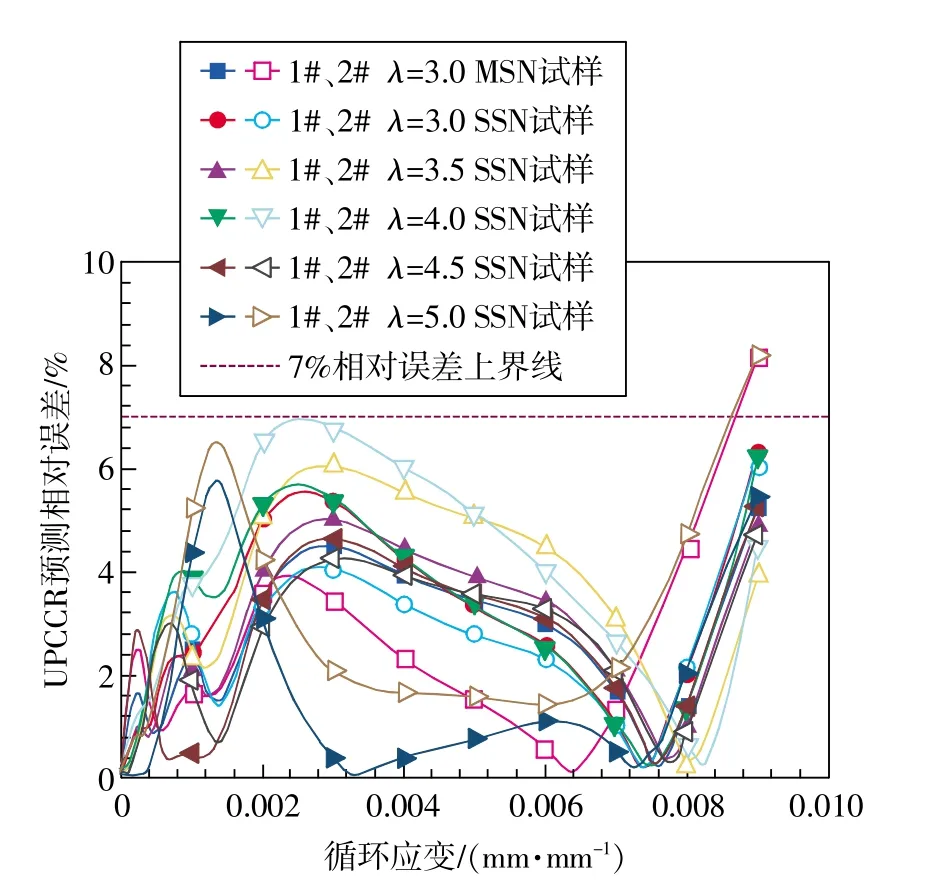
图21 316L不锈钢循环应力-应变关系预测误差

式中i=1～6，1 表示 MSN 试样、2～6 表示λ=3.0，3.5，4.0，4.5，5.0的 SSN 试样。

可以看出，相对误差δ基本在7%以内，说明基于MSN试样和不同λ值SSN试样采用循环应力-应变关系模型针对SS 316L循环应力-应变关系的预测精度93%以上。那么，可采用新模型用于毫小薄片材料循环应力-应变关系的准确获取。

4 结束语

1）创新设计了用于毫小薄板材料的低循环试验的MSN型试样和加载工装。

2）提出了一种基于毫小薄片漏斗试样循环稳定阶段的载荷-位移曲线预测材料循环应力-应变关系的原创性分析模型，在给定尺寸范围内，模型预测结果与有限元分析结果符合良好。

3）完成了316L不锈钢SRB型试样、MSN型试样和5种尺寸下SSN型试样应变对称的变幅低循环试验，获得了316 L不锈钢的循环应力-应变关系、MSN型试样和SSN型试样循环稳定阶段PLc-hc曲线。

4）应用新模型预测的6种几何尺寸下316L不锈钢薄片漏斗试样的循环应力-应变关系和SRB型试样试验结果在较小分散带内。误差分析表明，新模型预测精度在93%以上，从而试验验证了新方法的有效性。

[1]金属材料轴向等幅低循环疲劳试验方法：GB/T 15248-2008[S].北京：中国标准出版社，2008.

[2]Metallic materials-fatigue testing-axial strain-controlled method：ISO12106-2003[S].International Organization for standardization，2003.

[3]HE C，HUANG C，LIU Y，et al.Effects of mechanical heterogeneity on the tensile and fatigue behaviours in a laser-arc hybrid welded aluminium alloy joint[J].Materials&Design，2015（65）：289-296.

[4]YE S，ZHANG X C，TU S T.Interaction between local plastic strain and multi-scale fatigue crack propagation behavior in titanium alloy TC4[J].Applied Mechanics and Materials，2017（853）：51-56.

[5]WISNER S B，REYNOLDS M B，ADAMSON R B.Fatigue behavior of irradiated and unirradiated zircaloy and zirconium[C]∥Zirconium in the Nuclear Industry：Tenth International Symposium.ASTM，1994.

[6]李丹柯，蔡力勋.锆合金薄片材料高温低周疲劳试验技术[J].试验技术与试验机，2007（4）：16-20.

[7]蔡力勋，叶裕明，高庆，等.Zr-4合金薄片材料的应变疲劳与寿命估算[J].西安交通大学学报，2004，38（1）：97-104.

[8]叶裕明，蔡力勋，李聪.Zr-4合金小试样高温疲劳行为研究[J].核动力工程，2006，27（3）：37-42.

[9]蔡力勋，范宣华，李聪.高温对Zr-4合金低循环行为的影响[J].航空材料学报，2004，24（5）：1-6.

[10]CAI L X，YE Y M，LI C.Low-cycle fatigue behavior of small slice specimens of Zr-4 alloy at elevated temperature[J].Key Engineering Materials，2006（324/325）：1241-1244.

[11]黄学伟.新结构材料力学行为的获取方法[D].成都：西南交通大学，2010.

[12]黄学伟，蔡力勋，包陈，等.Zr-Sn-Nb薄片合金高温低周疲劳行为[J].原子能科学技术，2010，44（1）：60-64.

[13]黄学伟，蔡力勋，梁波.基于单轴缺口试样的一种低周疲劳测试方法与应用[J].中国测试，2009，35（5）：7-10.

[14]贾琦.异型试样疲劳与断裂性能测试方法研究与应用[D].成都：西南交通大学，2011.

[15]贾琦，蔡力勋，包陈.考虑循环塑性修正的薄片材料低周疲劳试验方法[J].工程力学，2014，31（1）：218-223.

[16]CHEN H，CAI L X.Theoretical model for predicting uniaxial stress-strain relation by dual conical indentation based on equivalent energy principle[J].Acta Materialia，2016（121）：181-189.

[17]HUTCHINSON J W.Singular behaviour at the end of a tensile crack in a hardening material[J].Journal of the Mechanics and Physics of Solids，1968，16（1）：13-31.