避开无穷 返璞归真（下）

张景中 彭翕成

5.不用极限定义导数

无穷在数学中的应用，在微积分学中达到了极致。

微积分中用到了无穷分割、无穷接近、无穷大和无穷小、无穷数列和无穷级数。无穷过程成了家常便饭。

拉格朗日的《解析函数论》一书的副标题是：“不用无穷小，或正在消失的量，或极限与流数等概念，而归结为有限的代数分析的艺术。”他用泰勒展开式克服极限理论的困难，这当然无法避开无穷。

拉格朗日时代至今已有200多年，避开无穷来建立微积分的想法依然徘徊在人们心头，挥之不去。网上有一本热销书叫做《Calculus Without Limits-Almost》。美国麻省理工学院的M. Livshits教授提出了不用极限定义导数的方法，还在自己的网站上销售带有Calculus Without Limits字样的T恤衫。

在中国，林群院士是改革微积分基本理论的倡导者。他提出用“一致性不等式”直接定义导数（参看林群著《微积分快餐》），从而在微积分的最基本的概念层次上避开了无穷。

林群的导数定义，可以形式化地表述如下：

用一致性不等式定义导数设函数F在[a，b]上有定义，如果有一个在[a，b]上有定义的函数f，和一个在（0，b-a]上正值递增而无正的下界的函数a（x），使得对[a，b]上任意的x和x+h，有下列不等式：|（F（x+h）-F（x）-f（x）h）|≤|h|a（h），则称F在[a，b]上一致可导，且称f是F的导数。

本文作者之一在《直来直去的微积分》一书中提出了另一个思路：用不同于牛顿的观点分析瞬时速度问题。

如何求任一时刻的速度，即所谓的瞬时速度呢？

牛顿让时间区间趋于0，启用了一个无穷过程。

能不能避开无穷来思考瞬时速度的概念呢？平均速度与瞬时速度有何关系？有没有简单明白的说法？

眼前就有一个明摆着的道理：在匀速运动时，瞬时速度就是平均速度；若不是匀速运动，瞬时速度有时比平均速度大，有时比平均速度小。

这里并没有回答什么是瞬时速度。这里只说，如果有所谓的瞬时速度，它应当有这样的性质，它和平均速度应当有这样的关系。

这样的说法平凡清楚。奇怪的是，数学家长期以来都忽略了这个平凡的关系。沿着这个平凡的思路，就能够避开无穷而走进微积分的大门。

如果用牛顿的思路，让两点无穷接近取极限，不少有用的信息就会被湮没。为了复原被湮没的信息，必须进一步研究无穷过程所产生的结果的性质，即极限的性质。而若从“瞬时速度有时比平均速度大，有时比平均速度小”这一点出发，则避开了求极限的无穷过程，保留了g（x）=2x与S（x）= x2的原汁原味的关系。与极限方法相比，可说是返璞归真。

6.避开无穷定义瞬时速度

“瞬时速度有时比平均速度大，有时比平均速度小”的道理，仅仅给出了瞬时速度应当满足的必要条件，并不是瞬时速度的定义。

能不能避开无穷过程，给瞬时速度一个看起来更有道理的定义？

先问一下，要瞬时速度有什么用？

速度是位移和时间的比。速度定了，可以根据时间求位移，就可以了解物体的运动状态。如果瞬时速度仅仅适用于瞬時，仅仅适用于长度为0的时间区间，就不能用它求出非0的位移，不能用它了解物体的运动状态，就没有用。如果想用瞬时速度，就要在一个长度非0的区间上用它。也就是说，在某个时刻T附近的小小的时间区间上，把运动的物体近似地看成以T处瞬时速度为速度的匀速运动。

当然，我们希望这样的匀速运动在小小的时间区间上是最接近真实运动的匀速运动。

瞬时速度的物理定义设S=F（t）是质点A的运动方程，若作匀速运动L（t）=F（u）+v（t-u）的质点B比任意一个匀速运动K（t）=F（u）+k（t-u）的质点C在时刻t=u附近更接近A，则称v为A在t=u处的瞬时速度。

其准确含义是指有一个包含u的时间区间I=（u-c，u+c），使得对一切t沂（u-c，u+c）但t屹u（t=u时，L（u）=F（u）=K（u）），总有|L（t）-F（t）|<|K（t）-F（t）|。

应用极限理论和导数的性质，可以证明瞬时速度的物理定义和依赖极限的数学定义是等价的。

仅仅应用瞬时速度的物理定义容易推导出，若运动方程为S（x）=x2，则时刻x的瞬时速度为g（x）=2x。这时|L（t）-F（t）|<|K（t）-F（t）|中的L（t）=u2+2u（t-u），K（t）=u2+k（t-u）。而F（t）=S（t）=t2。要证明的是有一个包含u的时间区间I=（u-c，u+c），使得对一切t沂（u-c，u+c）但t屹u（t=u时，L（u）=F（u）=K（u）），总有|u2+2u（t-u）-t2|<|u2+k（t-u）-t2|。

设t屹u，约去|t-u|后成为|u-t|约|k-t-u|。注意条件k屹2u（否则两端恒等），可以记k=2u+d，要证的不等式化简为|u-t|约|u-t+d|，当|u-t|足够小时此式当然成立。

7.避开无穷定义切线

数学家经过一千多年的思考才认识到，切线是割线的极限。沿着这个线索发现了导数，启动了创建微积分的“大业”。

但是，极限是分析的概念，涉及一个无穷过程。能不能避开无穷，不依赖分析中的极限概念，建立切线的几何定义呢？

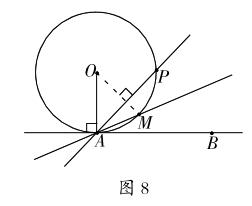
最早研究的切线是圆的切线，看看圆的切线有何特点。

如图8，过圆O上一点A作切线AB，再作圆O的任意一条割线AP。设直线AM是蚁PAB的角平分线。显然，在切点A附近，切线比任意一条割线更接近圆弧。

可以说，在过切点的所有直线中，在切点附近最接近圆弧的是切线。这启发我们给出不依赖于极限的切线的定义。

曲线切线的几何定义过曲线上一点A的所有直线中，如果有一条在点A附近最接近该曲线，就把这条直线叫做该曲线在点A的切线。

应用极限理论和导数的性质可以证明，切线的几何定义和微积分中用极限建立的定义是一致的。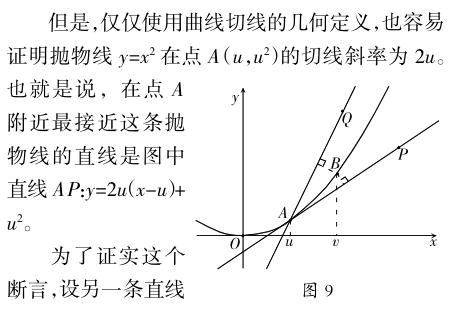

因为当k≠2u时，d≠0，容易看出当|h|足够小且非0时，有d（B，AP）

这里按照切线的几何定义来确定某条直线是不是切线，比起硬性规定切线就是割线的极限，则显得更为简单和顺理成章，也使我们获得了更多信息和更深刻的认识。这又是避开无穷带来的意料之外的收获。

8.避开无穷求导数

上面几节以函数y=x2为例，探讨了在微积分中避开无穷的可能。

新思路来自一个常识性的断言：瞬时速度有时大于或等于平均速度，有时小于或等于平均速度。

为了方便更一般的讨论，下面把这个思路提升为数学概念。

确实可以。容易证明：若g（x）是f（x）在区间I上的乙函数，又是f（x）在区间J上的乙函数，且区间I和区间J有公共点，则g（x）是f（x）在区间K= I胰J上的乙函数。

用了估值不等式，从乙函数的性质马上可以推导出甲函数的性质：

（i）若乙函数恒为0，则甲函数为常数；

（ii）若乙函数为非0常数，则甲函数为一次函数；

（iii）若乙函数在某区间上恒正，则甲函数在此区间上递增；

（iv）若乙函数在某区间上恒负，则甲函数在此区间上递减。

从这些性质看，乙函数很像导数。但从导数的定义推导出这些性质是一个很痛苦的过程：先要走进无穷世界，再从无穷世界解脱出来回归现实，好像经历了一次脱胎换骨的轮回。而避开无穷使用估值不等式，简单明白地就得到了这些性质。甲、乙函数概念的建立，可以看成是微积分基本思想的返璞归真。

容易提出问题，满足不等式的甲、乙函数相对来说是唯一的吗？

从定义确实不能保证乙函数的唯一性。对所讨论的函数类加一些限制条件是必然选择，如差商有界；甚至可以加一个更弱的条件：一致連续。限于篇幅，在此就不展开论述了。其实还可以避开无穷求面积，导出微积分基本定理，建立一元微积分的基本理论，有兴趣的读者可参看《不用极限的微积分》和《直来直去的微积分》两本书。

无穷大和无穷小都是人们想象力的创造物。有了无穷的概念，数学家有时能够更方便地发现、解决或描述只涉及有穷的问题。数学能够思考无穷，而且能够得出一系列令人信服的有关结论，是理性思维与感性直观相互融合渗透的典型范例。

微积分是人类精神的胜利之果，是两千年来人类智慧的结晶。它既包含了基于潜无穷的极限方法，也包含了基于实在无穷小的非标准分析方法。如今我们可以看到，它还有避开无穷的朴素的方法。这显示出微积分学的丰富多彩，让我们又一次感受到数学文化的博大精深。

（作者单位：中国科学院华中师范大学）