运用函数图像法 巧解导数压轴题

郑政波

（古田县第一中学，福建 古田 352200）

导数综合题其所含知识往往涉及函数、导数、方程、不等式等众多高中数学主干知识，解题方法往往要综合和灵活运用函数与方程、化归与转化、数形结合、分类与整合、构造法、分离参数法等数学思想方法，加上函数在中学数学中的特殊地位，因此这类题成了全国高考数学各省市试题的“常客”。这类题用常规思路和方法求解，要么过程繁杂，要么运算复杂。学生只好望题兴叹。

在多年的高三数学专题复习教学中，笔者在让学生熟悉解决这类问题的常规思路和方法的基础上，引导学生总结出了一套应对［1］零点、恒成立求参数、证明一些不等式问题难通甚至不通时的求解策略：分类构造函数图像法。

例 1（2013年新课标 2理 21）已知函数 f（x）=ex-ln（x+m）

（1）设 x=0 是函数 f（x）的极值点，求 m，并讨论f（x）的单调性；

（2）当 m≤2 时，证明 f（x）＞0。

解析：（1）略；（2）因为 m≤2，所以 x+m≤x+2，ln（x+m）≤ln（x+2）而函数 y=ln（x+2）的图像上凸，在点（-1，0）处的切线方程为 y=x+1，所以 ln（x+2）≤x+1（当且仅当x=1时取等号），又因为函数的图像下凸，在点（0，1）处的切线方程为 y=x+1，所以 ex≥x+1（当且仅当 x=0 时取等号），所以 ex≥x+1≥ln（x+2），因为等号不能同时取到，所以ex＞ln（x+2），于是得 ex＞ln（x+m），所以 f（x）=ex-ln（x+m）不等式得证。［2］

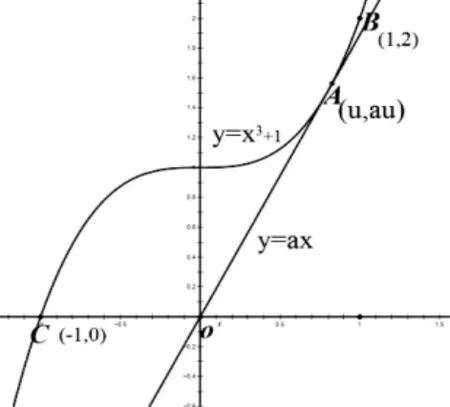
图1

点评：本例第（2）问，函数 f（x）由函数 y=ex与 y=ln（x+m）两部分构成，函数图像比较熟悉，借助函数y=ex在（0，1）点切线与函数y=ln（x+2）在点（-1，0）处的切线方程都是 y=x+1 的特殊性，从而完美地利用数形结合解决问题。这种切线法解题高效、简洁其本质实际上就是：半分离参数的函数图像法。通过移项、适当变形构造两侧较为特殊函数图像。请看下例：

例 2 当 x∈［-1，1］时，不等式 x3-ax+1≥0 恒成立，则a的取值范围是______

试题分析：对 x3-ax+1≥0学生基本上先通过分类讨论，再用分离参数法解决。

解析：当x=0时，不等式化为1≥0，恒成立，所以a∈R。

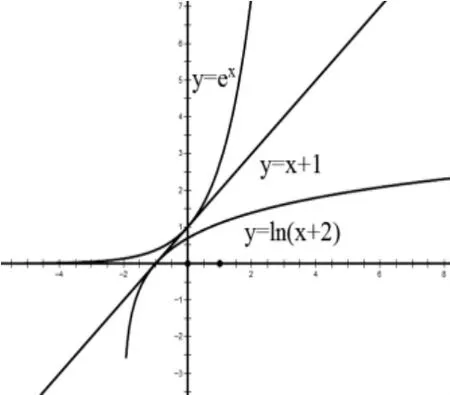
图2

点评：分离参数法是常用的解题方法，主要是为了避免对字母的讨论。该例还可以通过对不等式移项得：x3+1≥ax，看到了例 1 的影子。 作出函数 f（x）=x3+1图像，而函数是 g（x）=ax过原点的一条直线，当 g（x）与 f（x）相切于 A 点时 a值最大，设切点坐标 A（u，au）（如图2），利用解得a=随着 a值的改变，直线 g（x）=ax 绕着原点转动，又因为 x∈［-1，1］，数形结合可知斜率（详解过程略）

点评：不一样的角度解题，切线法与分离参数法相比，有它独特的几何美感，这种美的享受自然是建立在对基本函数图像熟悉的基础上，但有时方程组的解法会随着曲线 f（x）的复杂（如 f（x）含有ex，lnx等）而变得更加灵活。

例3（2010年全国卷第21题）设函数f（x）=ex-1-x-ax2.

（1）若a=0，求 f（x）的单调区间；（2）若当 a≥0 时f（x）≥0，求 a 的取值范围.

图3

试题分析：（1）略；

（2）观察到函数 f（x）=ex-1-x-ax2由几个初等函数构成，因为 f（x）≥0，适当移项把含参数项归到一侧，左右两边即可构造两个函数。移项原则上对含参数项构成的函数易由参数控制，不会造成函数图像繁杂的讨论。

解析:∵x≥0 时 f（x）≥0

∴ex-1-x≥ax2令 h（x）=ex-1-x，g（x）=ax2则 h＇（x）=ex-1，因为 x≥0，所以 h＇（x）≥0，又因为 h＇＇（x）=x2＞0，所以函数 图像下凸，利用导数作出函数h（x）图像（如图 3）。

当 a≤0 时，g（x）=ax2图像都在函数 h（x）图像下方，所以a≤0符合；

当 a＞0 时，抛物线 g（x）下凸且 h（0）=g（0）=0，即函数 h（x）与 g（x）图像是共起点的两条下凸曲线，所以 h＇（x）≥g＇（x），即当 a≥0 时 ex-1≥2ax 恒成立，令 φ（x）=ex-1，m（x）=2ax（a＞0，x≥0）作出图 4，因为 φ（x）=m（x）=0，所以当 x≥0 时，φ＇（x）=m＇（x）恒成立，所以，当 x≥0 时，ex≥2a 恒成立，所以 1≥2a，即 a≤综上a≤.

点评：本题图像由同起点两条下凸曲线构成，通过同时对两边函数一阶导等价转化解题。由f（x）≥0移项转化为：ex-1-x≥ax2还是 ex+1≥ax2+x，哪种构造更好，需要对基本函数图像有较为深刻的理解，除了几个初等函数外，依笔者经验还需要对xex，xlnx，，等函数图像有一定的掌握。如下例：

例4（2017高考全国卷1理21题）已知函数f（x）=ae2x+（a-2）ex-x.

（1）讨论 f（x）的单调性；（略）

（2）若 f（x）有两个零点，求a的取值范围.

图4

试题分析：（2）问中f（x）有两个零点，转化为方程 f（x）=0 有两解，移项得 aex+（a-2）=。得到两个较为特殊函数 h（x）=aex+（a-2）与 g（x）=，因为 g＇（x）=，所以 x＜1 时，g（x）单调递增，x≥1 时，g（x）单调递减，又因为 x→+∞，g（x）→0+，x→-∞，g（x）→-∞，且g（0）=0，g（x）max=g（1）=。 在坐标系中作出函数g（x）图像，当 a=0 时， h（x）=-2 与函数 g（x）图像有且只有一个交点，不符题意。

图5

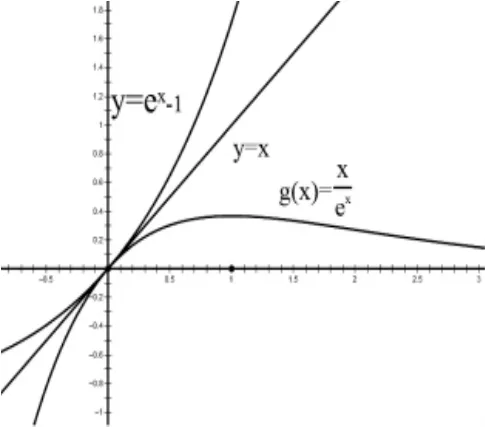
图6

点评：移项变形后出现了 h（x）=aex+（a-2），g（x）=较为特殊的函数，从而能顺畅地利用两个函数图像直观解题，借助图形轻松抓住a=1后，利用两函数图像的公切线为y=x这个关键点，从而达到解决问题目的。这是需要平时对特殊函数图像深入了解的积累，也要求一线教师重视对初等函数的教学，尤其高考压轴题常常涉及ex，lnx与一次函数的乘除组合函数，它们的图像利用导数知识易画出。当然分离两函数方法优劣，决定着解题的成败。下面笔者给出分离构造成两个函数的三个原则：参数同侧原则；分离出的两函数图像能借助导数容易作出原则；含有ex，lnx项最多与一次函数积或商的结构原则。其中原则一是基础，原则二是关键，原则三是难点。

下面再以几例高考题说明这个问题。

例 5 （2016 全国卷 1）（21）已知函数 f（x）=（x-2）ex+a（x-1）2有两个零点。

（1）求a的取值范围；

（2）设 x1，x2是 f（x）的两个零点，证明：x1+x2＜2（略）

（1）试题分析：函数 f（x）=（x-2）ex+a（x-1）2有两个零点。所以方程 f（x）=0 有两解。移项得 a（x-1）2=（x-2）ex，左右两边就是两个函数的较好模型，不需再考虑两边是否同除以2-x进一步分离出ex。利用导数作出函数 y=（2-x）ex图像。易知 x=1 是函数 y=（2-x）ex极大值点，抛物线对称轴是直线x=1（如图7）。通过讨论a＜0，a=0，a＞0，观察图像极易得到本题答案 a＞0。

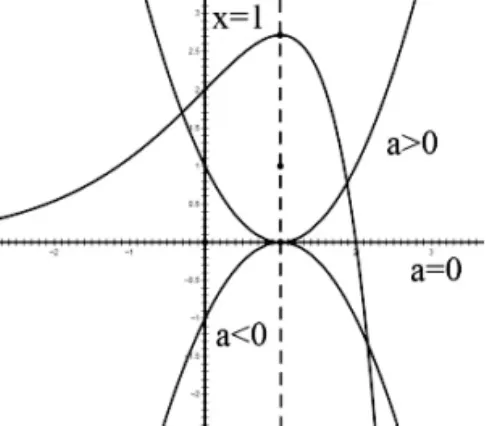
图7

图8

例 6 （2014 全国卷 1）（21）设函数 f（x）=aexlnx，曲线 y=f（x）在点（1，f（1））处的切线为 y=e（x-1）+2。

（Ⅰ）求 a，b；（Ⅱ）证明：f（x）＞0。

试题分析：（Ⅰ）略

（Ⅱ）由（Ⅰ）知a=1，b=2，证明 f（x）＞1，aexlnx+

点评：本例对函数模型exlnx分离，深度考查考生的函数图像知识，完成难度大，因为不借助几何画板不易作出函数y=exlnx的图像，所以必须分离。这就要求教师平日教学应注重渗透：几何直观理念，重视函数教学，充分挖掘简单组合函数图像，以形助数。该题导数压轴题考生得分率极低，因此适当的模型教学有助于克服考生对导数压轴题的恐惧心理。

综上可以看出，导数压轴题的命题注重以函数图像为载体，导数为工具来考查的方式。通过这些导数压轴题，反过来指导教师的导数教学。数学教育大家罗增儒先生说过“数学学习中真正发生数学的 地方都无一例外地充满着数学解题活动”，在这个解题思维的逻辑推理活动过程中，需要善于代数变形，诸如：移项、分解因式、配方、构造函数；需要几何直观，不妨画画函数的草图，或方程对应的曲线，通过可视化思维，实现有序的、合乎情理的、简洁数学逻辑推理。［3］

［1］黄学波.解函数与导数综合题时通法难通怎么办［J］.数学教学研究，2015（6）.

［2］张显文.例谈切线法解导数压轴题［J］.中学数学研究，2016（2）.

［3］安振平,袁义东．高考函数压卷题的解题与命题剖析［J］．中学生理科应试，2016（11）.