高中数学解析几何中数形结合思想生成过程探析——由一道竞赛试题引发的思考

周明亮

（宁化县第六中学，福建 宁化 364200）

解析几何是高中数学中不可或缺的重要知识点，在培养学生缜密思维、整体把握题意方面具有不可替代的作用。它一般要借助直角坐标系，通过代数运算的手段，研究包括椭圆、双曲线、抛物线等在内的圆锥曲线的概念、性质以及直线与圆锥曲线在平面内的位置关系等。解析几何的问题，一般来说，解题思路都比较清晰，解题方法和规律性也比较强；但对学生的计算能力、恒等变形能力、数形结合能力、化归与转化能力要求很高。因此，很多学生碰到解析几何题就倍感烦恼，繁杂的运算在很大程度上成为许多学生难以逾越的障碍。

一、从一次说题大赛说起

在一次教学基本功大赛的《说题》环节中，主办方提供这样一道解析几何的竞赛试题。

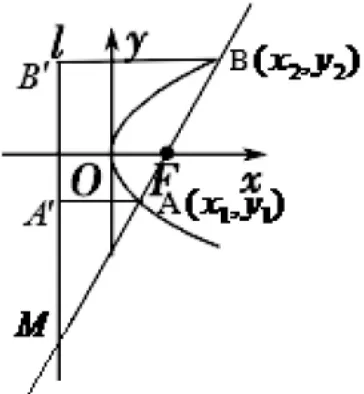
例1.抛物线y=4x，过焦点F的直线l交准线于M，交抛物线于 A、B 两点，且M→A=λ1A→F 、M→B=λ2B→F 试探究λ1+λ2是否为定值。

看到这题，笔者头脑中就已经形成了解题的基本思路：设直线方程→联立方程消元→由条件建立关系式求解。

具体解法如下：

解：∵y2=4x的焦点坐标 F（1、0），由题意 l的斜率一定存在，设l方程为y=k（x-1）代入抛物线方程得：

虽然，当时是很顺利地完成了解题过程，但是面对较复杂的圆锥曲线计算时，还是有点过于小心翼翼。因此，题目解完了，时间却也在不知不觉中过了不少。导致后续的其他《说题》环节就显得有些匆忙。这部分得分不是很理想，有些遗憾。

赛后反思这次比赛的得失，不禁让笔者思考起一个问题：一个教师，在解题思路清晰，解题过程也很顺畅的情况下，都用时不少。那么学生在高考那种紧张环境下，怎么做到快速、有效地完成解析几何的作答过程呢？

二、回归定义，数形结合，优化思维

赛后重新审视这一道题，笔者发现忽视了另一视角，即λ1，λ2的几何意义。结合抛物线的定义，另一种解法就形成了。如上图：

这一解法，将问题回归抛物线，“到定点距离等于到定直线的距离”这一定义，将转化为的长；再通过直角三角形中正弦定义，将 λ1，λ2用∠AMA＇，∠BMB＇的正弦表示。整个解题过程，几乎就没什么计算，步骤也少，效率自然也高了。因此，在今后的解析几何教学中，要让学生充分理解定义，并引导学生学会用定义解决有关问题。

同样，这道竞赛题也提示教师，教学中要重视培养学生观察图形、分析图形、运用图形的能力。特别是要重视圆锥曲线有关概念的几何性质。解决解析几何的问题这一基本思想方法，就是数形结合的方法，而圆锥曲线的定义往往又是数形结合思想的典范。因此，通过回归定义，数形结合，可以达到优化思维的目的。数形结合的重点在“形”，后一种方法就是在“形”的基础上得到的。数形结合的实质是数与形的一个映射。这里将抽象的数学语言如与直观的几何图形线段结合，再通过∠AMA＇的正弦这一个“数”建立联系。

因此，教师在教学中引导学生，充分认识到“数形结合”这一思想方法在解题中的应用。而笔者当时正是在解题中忽略了这点，只从代数角度去处理，使问题计算量大大增加。因此，平时的教学过程中，要让学生充分理解并灵活应用相关概念的几何意义，就显得尤为重要。因此，要在教学中积极地探索和渗透这一方法，并应用它来解决问题，使其能融入整个教学过程中，让学生能够具备多次理解、应用的机会。

三、通过对比，有意识地培养数学结合思想

数形结合思想的形成，进而有意识地运用，并不是教学中灌输的结果，而是学生在解题过程中通过对比、感受与体验后的选择。为此，教师在解题教学中，必须学会等待，学会让学生自然地认可“数形结合”。教师千万不要急于求成，把简洁的解法和盘托出，那样学生是体会不到“拍案叫绝”的解题效果的。

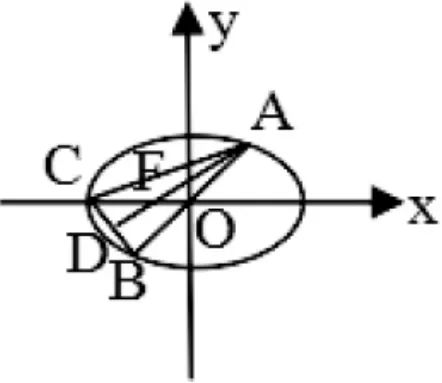
笔者让学生自己先动手、动脑解决问题。然后，从学生的解法中分析并列举两种学生的主要解法。

1.从直线方程入手：设直线AF的方程为y=k（x-1），联立椭圆，得A点坐标和B点坐标；得BC的中点D的坐标，代入直线AF的方程求解。

2.从点的坐标入手：设点 A（x0，y0），由中心对称得B点坐标，再由B、C点坐标，得D点坐标。利用A、F、D三点共线求解。

这两种方法都是从代数的方法求解问题，思路也是清晰可行的。笔者首先肯定了他们的做法。但是整个解题过程繁杂，计算量大，计算出错的较多，解题效果并不理想。如何优化解法呢？学生一时陷入了沉思中。

这时，教师再引导学生从数形结合的角度去思考并解决问题，学生才能感受到数形结合思想的重要性。这时，顺水推舟给出第三种解法：

连接OD、AC，如图则OD为△ABC的中位线，OD//AC且，△ODF∽△CAF，得

由于该解法是如此的简洁，过程是这样的漂亮，给学生留下了深刻的印象，在今后的解题思路中就会对“数形结合”思想特别重视。

所以，数学教师在教学中，要尽力引导学生挖掘图形的几何特征，对“数”与“形”进行统一分析、思考，简化计算，提高解题效率和准确率。

四、通过数形结合下的变式拓展，挖掘母题的思维价值

课本中的例题、习题是编者反复斟酌、试验、比较、精挑细选的。作为“母题”，它适合于所教的知识和大部分的学生，具有较强的典型性和代表性，是培养学生学习能力主要素材，充分挖掘它的价值，可以让学习起到事半功倍的效果［1］。它对于促进学生巩固知识、形成技能、发散思维方面有不可替代的作用。所以，挖掘例题、习题的母题价值，能最大限度地提高学生学习的有效性。

例4：斜率为1的直线l经过抛物线y2=4x的焦点F，且与抛物线相交于A、B两点，求AB的长。

通常教师会给出两种思路：

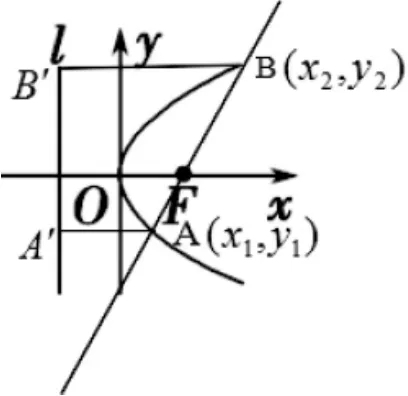
然后对两种方法进行比较。方法一：常见的通性通法，思路常规，但涉及较多的代数计算；方法二：回归定义，数形结合得出结果，计算较简单。解题方法看似很完美，有回归定义、数形结合；也有通性通法。但经过这次竞赛，笔者在这学期再备课时，总觉得意犹未尽。因为还没有结合数形结合思想很好地挖掘其母题的思维价值。因此结合练习、作业，在讲解完例4后，预设了让学生思考以下几个命题：

1.以AB为直径的圆与准线的位置关系是什么？怎样证明？

2.过弦AB中点作准线垂线，垂足为C，求证：∠ACB=90°。

3.直线l过y2=4x的焦点F，与抛物线交于A、B两点。求线段AB长的最小值。

4.（注意到方法1中x1x2=1）探究直线l过抛物线y2=2px 的焦点且与抛物线交于 A（x1，y1），A（x2，y2），那么x1x2和y1y2是定值吗？

通过这些变式训练让学生思考、讨论，收集解法和结论，并鼓励学生提出新的命题。结果发现，学生的兴趣更高了，数形结合的效果也得到充分的体现，更好完成了教学任务。

当然，培养学生掌握解析几何的各种题型解题的通性通法，始终是教师教学的主要任务。学生通过设点、联立、判别式、韦达定理等一系列计算过程训练，有利于养成固定的解题模式，有利于计算能力和整体思维能力的发展，也有利于解题速度的提升。因此，教学中要引导学生理解圆锥曲线相关的定义，理解相关知识的形成过程，特别是要培养学生有意识地利用“数形结合思想”简化计算，提高解题效率和准确率。在“数形结合思想”指导下，通过挖掘例、习题的潜能，变式拓展，使学生做到“做一题、通一类”，这样才能更有效提高学生解决解析几何的能力。

［1］卢春林．析初中数学教材中的例题与习题的重要性［J］．数理化解题研究（初中版），2014（10）.

［2］张艳.数形结合思想在高中数学教学中的应用研究［J］.中国校外教育，2016（11）.