集约简算法和改进遗传算法混合求解集合覆盖问题
陈向阳,李汪根,胡东辉
(1.安庆医药高等专科学校公共基础部,安徽安庆246052;2.安徽师范大学数学计算机科学学院,安徽芜湖241000;3.合肥工业大学计算机与信息学院,安徽合肥230002)
1 引言
集合覆盖问题是优化组合上的一个经典的NP-问题[1]。它已被广泛应用于电路优化设计、测试优化、车辆路径优化、网络节点选择、模式识别、人工智能、生物信息学等诸多领域。
国内外许多学者提出了大量的近似算法。如吴信东提出HVC算法[2-3],陈亮提出启发式遗传算法[4],连光耀提出基于粒子群优化算法的测试选择优化方法[5],葛洪伟提出基于SCHF的蚁群算法[6],崔鹏深入研究了关于集合覆盖贪心算法的最小测试集[7]。J.E.Beasley提出拉格朗日函数启发算法和遗传算法[8-9]。Alberto Caprara改进了拉格朗日函数启发算法[10]。Fisher和Kedia提出采用对偶启发式的最优解[11]。
任何集覆盖的近似解与精确解之间都存在一定的距离。1997年,Petr Slavik证明了逼近度ln(|S|)-lnln(|S|)+O(1)的贪心算法[12]。1998 年,Uriel Feige证明了不存在一个集合覆盖问题的多项式时间近似算法低于阈值(1-O(1))ln(|S|)[13]。
本文提出了一种集约简算法和改进遗传算法的混合方法,用于解决集合覆盖问题。模拟实验表明,当测试集的规模比原来的问题小十倍以内时集约简算法(SRA)效果明显。在全局搜索最小和收敛速度上改进遗传算法(MGA)具有明显的效果。
2 集约简算法(SRA)
2.1 基本概念
定义1覆盖网M{Φ,Ω;Γ},其中 Φ={Ei︱0≦i<n};Ω={Sj︱0≦j<m,Sj是集合Φ的子集,并且对于任意E属于Φ,其一定也属于Sj,即满足E∈Sj};Γ满足:如果Ei∈ Sj,(Ei,Sj)∈Γ。这样的三元组称为覆盖网。Φ叫做元素集,Ω是集合;Γ为接触组,n是计量,记为|M|;m是规模,记为||m||。(Ei,Sj)被称为接触。Γ中接触的数量被称为覆盖网M的复杂度,记为|||M|||。
集合[E]={S|(E,S)∈Γ}被称为元素E的属于集合,S的数量被命名为元素E的出度,记为|E|。当|E|=1时,[E]表示唯一一个元素S。
集合[S]={E|(E,S)∈Γ}被称为集合S的属于集合,E的数量被命名为集合S的入度,记为|S|。
集合<E>={E*|E*∈[S],S∈[E]} 被称为元素E的相邻集合。
W(S)= ∏ (1-1/|E|),当 E∈[S]时,W(S)被称为集合S的选定索引。
如果两个覆盖网M1和M2,其计量,规模和复杂度都是相等的,两个覆盖网中所有的元素和集合都一一对应,且两覆盖网中所有接触完全对应,则称M1和M2是同构的。相应的元素(或集合)被称为元素(或集合)的对应点。
定义2简化的覆盖网:覆盖网M{Φ,Ω;Γ},在Ω中两个不同的集合S1、S2,[S1]是[S2]的子集,集合S1可以收缩成集合S2,则S2称为集合S1的收缩点,表示为S1→S2,覆盖网M称为集合收缩网(SCN)。如果在Ω中有两个不同的元素E1、E2,[E1]是[E2]的子集,表示为E2→E1,元素E2可收缩成元素E1,则E1称为元素E2的收缩点,覆盖网称为元素收缩网M(ECN)。如果覆盖网M既不是SCN也不是ECN,M则是一个简化的覆盖网,表示为S1∽S2。如果E1→E2并且 E2→E1,则元素E1和E2相似,表示为S1∽S2。
定义3覆盖和最小覆盖:对于覆盖网M{Φ,Ω;Γ},集合C={Si|Si∈ Ω 和 ∪Si= Φ,i<||M||}称为覆盖网M的覆盖。集合C中S的数量称为覆盖的度,表示为|C|。如果|Least C|≤|任意覆盖|,LeastC就称为覆盖网M的最小覆盖。
2.2 集约简算法
Data←采用双十字链表存储的覆盖矩阵;ElementNumber←覆盖矩阵元素的数目;workele←所有元素;WorkSet←所有集合(因为在电路优化设计中所有的集合都有联系,所以一开始WorkSet是空);


3 改进的遗传算法(MGA)
标准遗传算法(SGA)的灵感来自于生物进化的机制,是一种高度并行的启发式搜索算法。它源于一个代表可行的解决方案的随机的人口的染色体,然后基于定义的适应度函数的每个个体都在人群中进行评估。更重要的是,通过使用一系列的遗传算子,如选择,交叉或突变产生新的一代。这个过程不断重复,直到满足停止准则。最后,最好的染色体被认为是最佳的解决方案。
由于SGA容易过早收敛,需要提高SGA以保证全局最优收敛。本文介绍了一种改进的遗传算法,特别地,操作参数进行了优化,并采用新的遗传算子,以提高其性能。MGA实现细节如下:
3.1 编码
编码是使用遗传算法需要解决的首要问题。采用二进制编码方案,选择的位置用1表示,不选的用0表示。
3.2 适应
适应的选择是MGA性能的关键。这里的性能是指对应于一个基因的列中包含1的个数。如果是一个大的数字则包含更多的行。它说明了该基因有相对高的性能。使用同样的方法,我们可以找到其他基因的覆盖集。为了找出最佳的染色体,需要考虑每个基因的成本。
适应度函数的描述如下:

其中r表示矩阵A的行;CJ表示第j列的成本。
3.3 遗传算子
三大遗传算子,包括选择、交叉和变异,其对遗传算法搜索效率有直接影响。在一些具体的问题中,选择适当的遗传操作参数是一个重要的问题。
(1)选择:这里采用的适应度比例法是轮盘赌选择法,这意味着染色体获得的适应度值越高,其被选择的概率就越大。本文中概率PSI有如下的表达式:
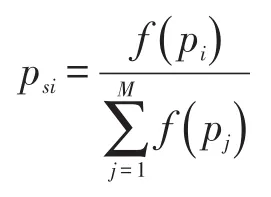
(2)交叉:交叉操作不仅可以从父母双方交流信息,而且可以产生与父母不同结构的更好的后代。应该注意的是,在这种情况下,在较少的迭代搜索中可以得到一个更高的适应值。使用一个改进的交叉算子。定义X1和x2为父母的字符串。因此,字符串x1和x2的后代被定义如下:
γ是区间[0,1]中的一个随机数。
(3)突变:突变的另一个关键因素是关于遗传算法的优化性能,可以保持种群的多样性,也有助于从父辈那里继承的特征。最重要的是,它使遗传算法能够用更好的适应度值来探索染色体。传统的遗传算法通常采用简单的变异和均匀的突变,因此,它导致局部搜索能力较弱。本文采用了一种特殊的技术组合变异算子和进化的一代,这起着进化精细调整的作用。用Xk表示一个父母,其在范围内,并假设后代的产生根据:
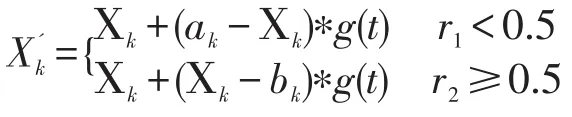
注意r1、r2是两个独立分布的随机变量,其范围是[0,1],t是当前迭代次数,T为最大的迭代次数。
为了防止种群的优良基因被破坏,采用动态突变概率确定的方法。当个体的适应度值大于平均值时,我们选择一个较小的变异概率,否则,选择较大的概率。
3.4 终止准则
确定MGA是否该继续运行:如果它达到停止条件的最大数量的迭代T,结束算法并输出最佳的权重和阈值。
4 案例研究
4.1 数据与变量
为了测试本文提出的混合SRA-MGA的影响,采用三组不同的数据集合,所有元素都是随机生成的。在第一个实验中的元素是8位的二进制数,研究在相同的比特位,但有不同的数据密度,所产生的效果。在这里,数据密度是指在同一位的元素的数量和样本空间的数量,如:在8位的样本空间的数目是256(2^8),如果选择其中的100个,密度就是100/256。第二个和第三个是不同的位,但都有相同的密度,数据密度分别为5/8和25/32。
这些测试集的详细信息如表1所示。
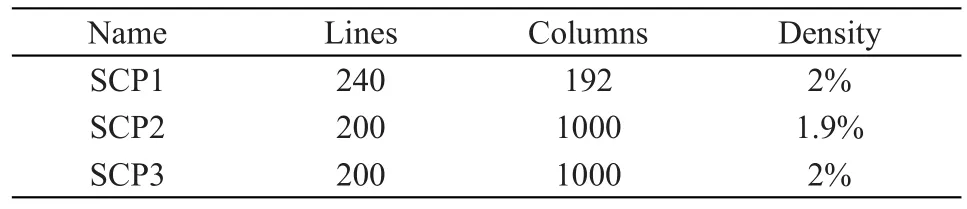
表1 测试集
4.2 实验结果和性能分析
不同的实验结果表明,在绝大多数情况下,SRA-MGA最小覆盖的算法比QM算法的小得多,并且SRA-MGA算法的选择集合更稳定。
对在QM和SRA之间SRA减少的集合数量的比较见表2。从表中可以清楚地看到,SRA引起的集数减少是QM的几倍或甚至几十倍。

表2 SRA-MGA和QM的性能比较
SRA-MGA和GA之间的最小成本比较如表3所示。从表中可以清楚地看到,SRA-MGA的表现比GA更好。

表3 SRA-MGA和GA之间的性能比较
5 结论
提出的结合SRA和MGA的混合模型继承了遗传算法的优势,克服其弱点。
从定理1和定理2得出,第一次的简化是先决条件,它的效果可以从实验结果得到。从遗传算法和SRA-MGA算法的比较中,选择最有可能的集合比选择最大出度的集合更有效。
本文的实验数据是随机的,但在实际应用中,验证效果还有待进一步研究。当元素与集合的数量很小时,SRA-MGA算法的解决方案是最小覆盖,但这一结论还没有被证实。如何更好地将SRA-MGA算法被应用在其他方面,以及如何改进,这些都是有待进一步研究的新问题。
[1]Michael R Garey.Computers and Intractability-A Guide to the Theory of NP-Completeness[M].Calif:W.H.Freeman&Co.,San Francisco,1979:71.
[2]吴信东.Optimiaztion problems in extension matrixes[J].Science in China Ser.A1992,35(3):363-373.
[3]吴信东.Inductive learning algorithms and frontiers[J].Artificial Intelligence,1993(7):93-108.
[4]陈亮,任世军.一种遗传算法在集合覆盖问题中的应用研究[J].哈尔滨商业大学学报(自然科学版),2006,22(2):67-70,114.
[5]连光耀,王卫国,黄考利等.基于粒子群优化算法的测试选择优化方法研究[J].计算机测量与控制,2008,16(10):1387-1389.
[6]葛洪伟,高阳.基于蚁群算法的集合覆盖问题[J].计算机工程与应用,2007,43(4):49-50.
[7]崔鹏,刘红静.测试集问题的集合覆盖贪心算法的深入近似[J].软件学报,2006,17(7):1494-1500.
[8]J.E.Beasley.A lagrangian heuristic for set-covering problems[J].Naval Research Logistics,1990,37(1):151-164.
[9]J.E.Beasley,P.C.Chu.A genetic algorithm for the set covering problem[J].European Journal of Operational Research,1996,94:392-404.
[10]Alberto Caprara,Matteo Fischetti,Paolo Toth.A heuristic method for the set covering problem[J].Operations Research,1999,47(5):730-743.
[11]M.L.Fisher,P.Kedia.Optimal solution of set covering/partitioning problems using dual heuristics[J].Management Science,1990,36:674-688.
[12]Petr Slavik.A Tight Analysis of the Greedy Algorithm for Set Cover[J].Journal ofAlgorithms,1997,25(2):237-254.
[13]Uriel Feige.A Threshold of ln n for Approximating Set Cover[J].Journal of theACM,1998,45(4):634-652.
[14]高阳.基于蚁群算法的集合覆盖问题求解及其应用研究[D].无锡:江南大学,2007:41-43.
[15]冯富宝.集合覆盖问题研究[D].济南:山东大学,2006:21-30.
[16]叶静.大规模数据集逻辑逆向综合关键算法的研究[D].郑州:解放军信息工程大学,2009:55-65.
[17]赵大胜.无线传感网络广播与节点休眠算法中的节能覆盖问题研究[D].武汉:华中科技大学,2005:81-86.

