二次侧非能动余热排出冷凝器传热计算研究①

刘翠波 杨锦春 刘敏华

(深圳中广核工程设计有限公司)

非能动系统是三代核电技术的主要特点之一，该特点能保证当核电厂丧失正常和备用电源时，会以非能动的方式将反应堆的余热导出，保证反应堆的安全性。二次侧非能动余热排出冷凝器(Secondary Passive Residual Heat Removal Condenser，简称SPRHR冷凝器)浸没于高于蒸汽发生器的高位水箱内，用于在严重事故下冷凝蒸汽发生器二次侧的蒸汽，冷凝器管侧产生的冷凝液依靠自身重力回流至蒸汽发生器二次侧，同时将热量传递至管外水箱中的水中，与蒸汽发生器相连的冷凝器管侧形成非能动循环，以此连续不断地排出反应堆产生的热量。

SPRHR冷凝器管内为冷凝换热，管外为池式沸腾传热，管内外均为相变换热，传热机理较为复杂。对于冷凝和沸腾传热，一般是依据基本物理模型，结合试验数据，获得半经验半理论的准则关系式，将该准则关系式用于换热器热工计算[1]。有关二次侧非能动余热排出冷凝换热器倾斜和竖直管内蒸汽凝结传热计算的报道较少，并且大都采用RELAP5或FLUENT等程序进行模拟计算。目前尚未有针对SPRHR冷凝器管内冷凝传热和管外沸腾传热耦合后传热计算方法研究的文献。

笔者通过试验数据，分析筛选出适合SPRHR冷凝器的传热准则关系式，并将根据准则关系式计算得到的传热系数和试验得到的传热系数进行比较。

1 SPRHR冷凝器传热分析

如图1所示，SPRHR冷凝器的换热器呈C型，倾斜段内的两段传热管与水平面呈5°倾角，传热管束整体浸没在水面之下，蒸汽发生器二次侧的蒸汽进入传热管入口管箱，在沿传热管长度方向逐渐被冷凝，冷凝方式为管内的膜状凝结。管内蒸汽的流向可以保证蒸汽和液膜同向流动，蒸汽流动会促使液膜变薄、传热系数增大[1]。传热管外侧为池式沸腾，SPRHR冷凝器需要将管外沸腾传热设计在核态沸腾区。由于核态沸腾的传热机理非常复杂，目前实验室获得的众多准则关系式往往有特定的适用范围[2]，因此在进行SPRHR冷凝器的热工计算时，首先需要选择与该冷凝器传热模式相匹配的传热准则关系式，保证冷凝器热工计算的准确性，其次需要设计合理的热工计算流程，综合考虑传热管内外参数的耦合影响，得到各个热工工况下SPRHR换热器的传热系数，进而确定合理的换热面积。

2 管内和管外传热准则关系式确定

2.1 管内冷凝传热准则关系式

由于SPRHR冷凝器的传热管由两段5°的倾斜段和一段竖直段组成，难以用单一的竖直管内膜状冷凝或水平管内膜状冷凝来表征，笔者选择Shah管内冷凝传热准则关系式来计算SPRHR冷

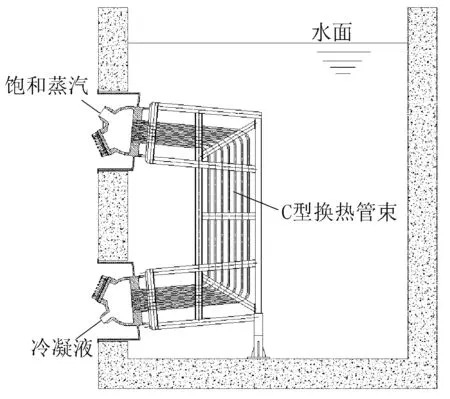
图1 SPRHR冷凝器示意图

凝器的管内冷凝膜传热系数。

Shah准则关系式综合考虑了474个试验点数据，适用于水平、竖直和倾斜管的管内冷凝换热，计算平均偏差为15.4%[1]。该公式已经在工程上得到了广泛应用，被认为是预测管内冷凝膜传热系数最为准确的关系式[3]。Shah准则关系式的物理模型是：管内凝结换热系数应等于管内单相流动时的换热系数乘以两相流动的修正系数，该修正系数取决于蒸汽的干度和对比压力。Shah准则关系式针对全凝结工况(入口处全部是蒸汽，出口全部是凝结液)和部分凝结工况(入口处有部分液体或出口处有部分液体)，具体表达式如下[4]：

(1)

(2)

式中a——管内膜状凝结换热系数，W/(m2·℃)；

al——假定质量流量等于气液两相总质量流量时液体在管内的单相对流换热系数，W/(m2·℃)；

pc——水的临界压力，MPa；

pt——蒸汽表压，MPa；

Shah准则关系式的适用范围如下：

对比压力R0.002～0.440

饱和温度Ts294～583K

蒸汽流速uv3～300m/s

蒸汽干度x0～100%

热流密度q158～1 890 000W/m2

质量流率Gi10.83～210.60kg/(m2·s)

液体普朗特数Prl1～13

SPRHR冷凝器系列工况参数基本在上述适用范围限值内，因此其热工计算可用Shah准则关系式。

2.2 管外池式核态沸腾传热准则关系式

学者Rohsenow认为池式气泡沸腾，主要是由于气泡生长脱落促成的边界层液体的扰动和冷热介质置换所引起的微对流造成的，其机理和单相对流换热机理类似，因此建议用Rohsenow准则关系式描述池式沸腾传热特性[5]：

(3)

式中cpl——传热管外液体定性温度下的定压比热，J/(kg·℃)；

C——系数，无量纲，对于不同介质与加热面金属的配合，C有不同值；

K——指数，介质为水时K=1.0；

Δp——传热管外壁饱和压力与传热管外水的饱和压力的差值，Pa；

Tw——金属壁温，℃；

λl——传热管外液体定性温度下的导热系数，W/(m·℃)；

μl——传热管外液体在定性温度下粘度，Pa·s；

σ——传热管外液体在定性温度下表面张力，N/m。

为了提高Rohsenow准则关系式的精确程度，Foster H K和Zuber N提出用气泡后期生长速度dR/dt与气泡尺寸R作为气泡雷诺数中的定性速度和定性尺寸，并根据试验数据获得相应的常数值，最终推导得到Foster-Zuber准则关系式如下[6]：

(4)

式中abl——管外沸腾换热系数，W/(m2·℃)；

r——传热管外液体在定性温度和压力下的汽化潜热，J/kg；

Δt——传热管外管壁平均壁温与传热管外水的饱和温度差值，℃；

ρl——传热管外液体在定性温度下的密度，kg/m3；

ρv——传热管外蒸汽在定性温度下的密度，kg/m3。

Foster-Zuber准则关系式在计算池式核态沸腾时精度较高，在工程计算中得到广泛应用[5]。SPRHR冷凝器采用Foster-Zuber公式计算传热管外核态沸腾膜传热系数。

3 SPRHR冷凝器热工计算流程

SPRHR冷凝器的热工计算流程图如图2所示。

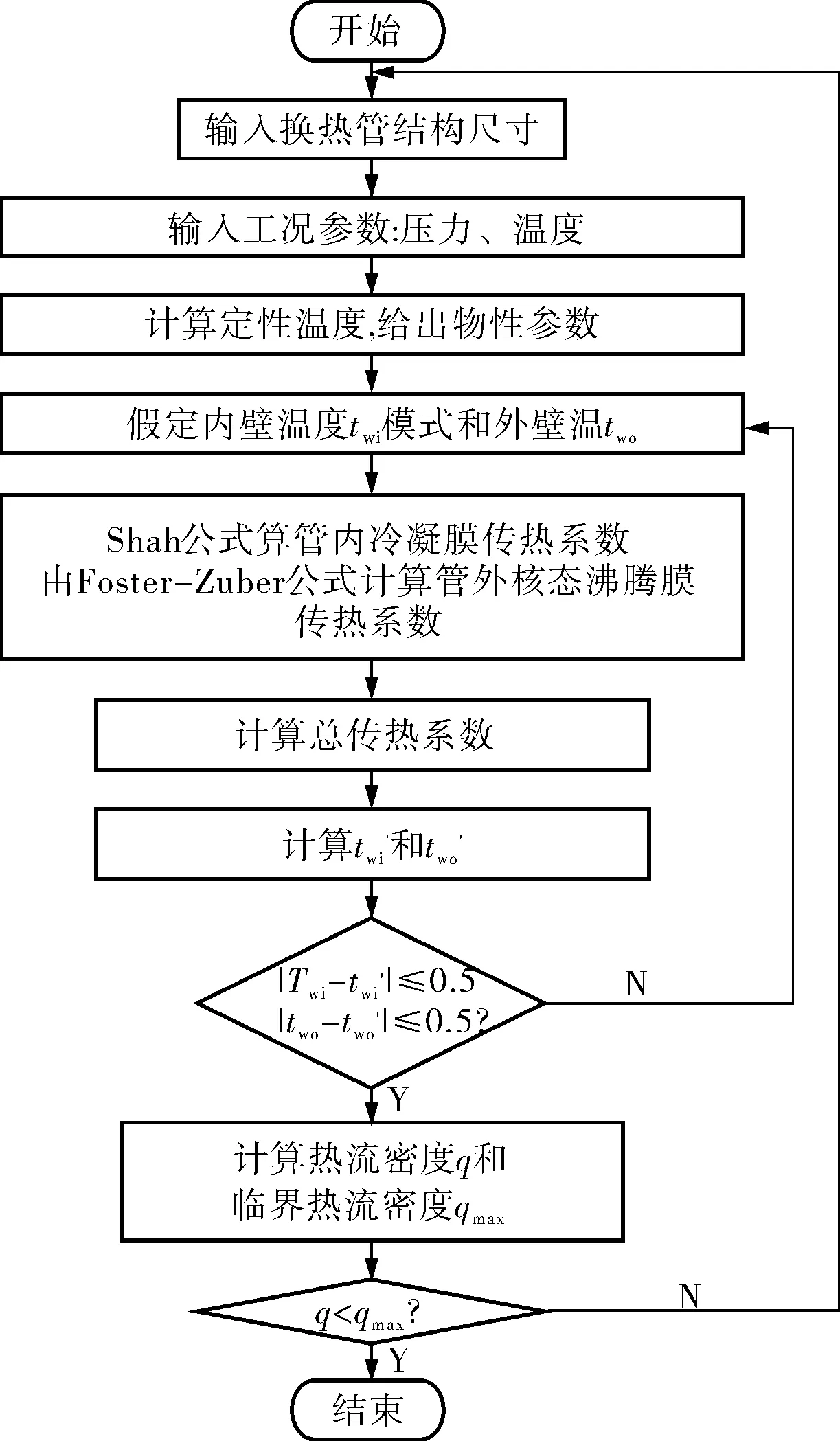
图2 SPRHR冷凝器热工计算流程

其中传热管内流体的定性温度tm为传热管蒸汽进口温度和传热管内管壁温度的加权值：

tm=0.25ti+0.75twi

(5)

式中ti——传热管蒸汽进口温度，℃；

twi——传热管内管壁平均壁温，℃。

传热管外流体进行池式沸腾，为饱和态蒸汽和液体混合物，忽略水位压差，其定性温度ts为标准大气压下水的饱和温度，ts=99.97℃。

传热管内壁平均壁温和传热管外壁平均壁温影响传热管内、外的物性参数，壁面过热度是传热管两侧膜传热系数的影响因素，而两侧膜传热系数又影响传热管由内至外的节点温度，因此需要迭代计算上述参数。SPRHR冷凝器总传热系数K0的计算公式如下：

(6)

式中abl——管外沸腾换热系数，W/(m2·℃)；

do——传热管外径，m；

δt——传热管壁厚，m；

λtm——管壁材料导热系数，W/(m2·℃)。

传热管内壁平均壁温和传热管外壁平均壁温需先进行假定，然后计算得到两侧的膜传热系数，进而计算得到管内壁和管外壁壁温，用计算壁温值代替假定壁温值，进行迭代计算，当壁温输入值和壁温计算值的差值绝对值小于0.5℃时，可认为壁温收敛。迭代计算传热管内壁平均壁温和传热管外壁平均壁温的计算公式如下：

(7)

(8)

式中two′——迭代得到的传热管外壁平均壁温，℃；

twi′——迭代得到的传热管内壁平均壁温，℃；

ΔT——管内、外总温差，℃。

SPRHR冷凝器的管外沸腾换热需要设计在核态沸腾区，因此需要将实际热流密度和核态沸腾临界热流密度进行对比，若实际热流密度大于临界热流密度，则需要对冷凝器的传热面积进行调整。

4 计算结果与试验数据对比

为了验证设备结构尺寸的可行性和理论计算的可靠性，开展了SPRHR冷凝器单根传热管传热试验，获取有关试验传热数据。

试验中采用蒸汽-水试验，将与工程换热管尺寸和结构相同的单根传热管淹没于大空间冷却水池内，开展传热与压降试验。试验中对管内流体的温度、压力、流量、管外冷却水池水体的压力及温度等参数进行测量。试验系统流程图如图3所示。

图3 SPRHR冷凝器传热实验系统

传热试验参数如下：

传热管规格φ48mm×3mm

传热管材料 316L

传热面积 1.1m2

管内蒸汽压力 3.0～8.6MPa

蒸汽入口温度 300℃

管内蒸汽流量 0.07～0.49kg/s

按照前述的计算方法，得到不同压力和管侧流量下SPRHR冷凝器的总传热系数，并与试验得到的传热系数进行了对比(表1)。

表1 传热系数对比

由表1可知，在不同蒸汽进口压力(8.6、6.0、3.0MPa)、不同管内蒸汽流量下，有13个计算点的理论计算传热系数和试验传热系数的相对误差在±10.0%以内。当蒸汽进口压力为3.0MPa、流量为0.070kg/s时，此时理论计算传热系数和试验传热系数的相对误差稍大，为-16.6%。

5 结束语

笔者根据SPRHR冷凝器投运后的换热工况，分析确定了适用于管内冷凝传热和管外池式沸腾传热的准则关系式，设计了SPRHR冷凝器的热工计算流程图，计算了与试验工况对应的总传热系数，并与试验传热系数进行对比，结果显示在14个计算工况下，有13个计算工况下的传热系数相对误差在±10.0%内，因此该计算方法准确度较高。目前该计算方法已经在SPRHR冷凝器实际工程设计中得到应用，满足工程项目设计要求。文中的计算方法和试验主要针对单根换热管，由于多根传热管组成的管束在进行沸腾换热时，管外核态沸腾换热受“管束效应”的影响，膜传热系数会有所增大，后续将针对该效应对传热的影响开展进一步研究和改进，以确定出管束传热的计算公式。

[1] 施明恒，甘永平，马重芳.沸腾和凝结[M].北京：高等教育出版社，1995.

[2] 李美琳，林萌，杨燕华，等.应用于反应堆热工水力程序的核态沸腾传热关系式评价[J].核科学与工程，2015，35(1)：25～31.

[3] 饶彧先，于雷，傅晟威.PRS换热器蒸汽凝结换热模型研究[J].核动力工程，2016，37(1)：34～37.

[4] Shah M M.A General Correlation for Heat Transfer During Film Condensation inside Pipes[J].Science Direct，1979，22(4)：547～556.

[5] 鲁钟琪.两相流与沸腾传热[M].北京：清华大学出版社，2002.

[6] Forster H K，Zuber N.Dynamics of Vapor Bubbles and Boiling Heat Transfer[J].AIChE Journal，1955，1(4)：531～535.