具Holling-type Ⅱ型功能反应的随机时滞捕食系统的研究

王晓燕， 董玲珍， 王素霞

(太原理工大学 数学学院， 山西 太原 030024)

0 引 言

在种群生态系统中, 捕食模型基于重要性及其广泛应用性, 已成为种群动力学模型的研究重点之一. 众所周知, 很多因素能够影响捕食模型中种群的动力学行为. 其中, 一个重要的因素是捕食者捕食食饵的能力, 也就是捕食者对食饵的捕食率, 即捕食者的功能性反应. 具 Holling-type 型捕食者的功能性反应依赖于食饵的密度[1], 若记食饵的密度为x1(t), 则捕食者对食饵的功能性反应可表示为数学上的函数关系Φ(x1(t))， 故具功能性反应且考虑到捕食者和食饵种群密度制约因素的捕食系统可被描述为数学模型(1)

(1)

式中：x1(t),x2(t) 分别表示食饵和捕食者在t时刻的种群密度;bi,aii(i=1, 2),k都是正常数,b1和b2分别表示食饵和捕食者的固有增长率,a11和a22分别表示食饵和捕食者种群内的密度制约作用,k表示捕食者的消化系数,Φ(x1(t))是捕食者对食饵的功能反应.

(2)

关于具Holling-type Ⅱ 型功能反应捕食系统的研究已经积累了丰富的成果, 可参阅文献[2-5].

在确定性种群动力学模型中, 我们常假设系统中的参数是确定的, 与环境的改变无关, 这导致所建立的数学模型有一定的限制, 理论结果很难与实际数据吻合, 故很难准确地预测这个系统未来的变化趋势. 事实上, 在种群生存的生态系统中, 不可避免地存在着环境噪音, 而环境噪音会影响种群的生存. 有很多文献已经引入随机模型来描述种群生态系统的进化过程. 文献[6-11]在确定性种群动力学模型中引入随机扰动, 建立了随机种群动力学模型, 分析了随机扰动对生态系统的影响. 另一方面, 在研究种群动力学行为的过程中, 我们也应考虑到时滞的影响. Kuang[12]提出忽略时滞意味着忽略现实. 文献[13,14]研究了具有时滞的捕食系统的一些性质. 本文将同时考虑时滞和随机扰动对具 Holling-type Ⅱ 型功能反应的捕食系统中种群动力学行为的影响. 为此, 我们建立随机时滞捕食系统

(3)

式中： dB1(t), dB2(t)是标准白噪声;B1(t),B2(t) 是定义在完备概率空间 (Ω,F,P) 上相互独立的Brown运动；ε1,ε2表示白噪声的强度；τ1,τ2表示时滞.

随机时滞系统(3)描述的是种群的动态进化过程, 从生物学的角度来看, 只有非负解才有生态学意义. 在本文中, 我们将通过选择适当的Lyapunov函数, 应用It公式, 首先讨论随机时滞系统(3)的一些基本性质, 即解的存在唯一性, 全局正解的存在性； 然后对解的随机最终有界性以及解的渐近矩估计进行研究.

1 全局正解的存在性

为了使一个随机微分方程对任意给定的初始条件具有整体解, 一般来说, 需要满足线性增长条件和局部Lipschitz条件. 但是, 随机时滞系统(3) 既不满足线性增长条件, 也不满足局部Lipschitz条件. 这里, 通过做变量替换, 应用It公式, 给出局部正解的存在性.

证明考虑系统

(4)

容易验证方程(4)的系数满足局部Lipschitz条件, 故方程(4)带有任意初始条件{(u(t),v(t))∶-τ≤t≤0}∈C([-τ,0];R2)的解在t∈[-τ,τe)上存在且唯一. 进一步, 对x1(t)=eu(t),x2(t)=ev(t)应用It公式, 可知方程(3)带有初始条件的解在t∈[-τ,τe)上存在且唯一.

接下来, 给出全局正解的存在性.

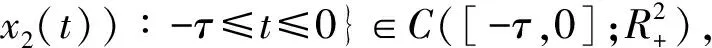
证明由引理1可知, 系统(3)存在唯一的局部解, 下证解的全局性.

下证τ∞=∞ a.s., 采用反证法. 如若不然, 假设τ∞≠∞, 则存在常数T>0和ε∈(0,1), 有

P{τn≤T}>ε.

因此, 存在整数N1≥N0, 使得

P{τn≤T}≥ε,n≥N1.(5)

[|x1(t)|2-|x1(t-τ1)|2+|x2(t)|2-|x2(t-τ2)|2]dt+

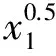
又因为

(7)

将式(7)代入式(6)中, 得

其中

易知,F1,F2都是有界的, 即

F1≤K1,F2≤K2.

所以

式(10)两端从0到τn∧T积分并取均值可得

因此

EV(x1(τn∧T),x2(τn∧T))≤

设1Ωn是Ωn的指标函数, 故

E[1Ωn(ω)V(x1(τn,ω),x2(τn,ω))]≥

令n→∞, 有

V(x1(0),x2(0))+(K1+K2)T≥+∞,

2 随机最终有界性

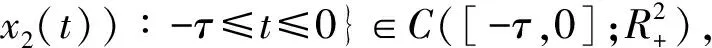
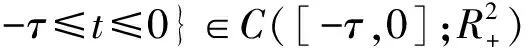
(13)

式中：H(θ)与初值无关.

证明定义

应用It公式, 得

dV(x1(t),x2(t))=LV(x1(t),x2(t))dt+

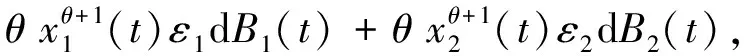
其中

由于0<θ<1, 故θ(1-θ)>0, 故

V(x1(t),x2(t))≤H1-V(x1(t),x2(t)),

其中H1是一个正数, 将其代入式(14)中, 得

dV(x1(t),x2(t))≤[H1-V(x1(t),x2(t))]dt+

再次应用It公式, 得

d[etV(x1(t),x2(t))]=

et[V(x1(t),x2(t))dt+dV(x1(t),x2(t))]≤

将式(16)两边从0到t取积分再求期望, 得

etEV(x1(t),x2(t))≤V(x1(0),x2(0))+

H1(et-1),

即

又因为

所以

故

进一步, 考虑解的随机最终有界性, 有如下性质成立.

定理2 系统(3)的解具有随机最终有界性.

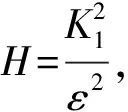
P{|(x1(t),x2(t))|>H}≤

故

3 解的渐近矩估计

定理1和定理2表明, 对任意给定的正初始条件, 系统(3)具有唯一的全局正解, 并且解是随机最终有上界的. 下面对解的渐近矩进行估计.

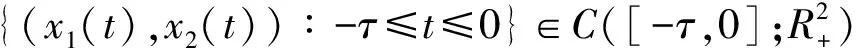
(17)

式中：K(θ)与初值无关.

证明令

则

dV(x1(t),x2(t))≤LV(x1(t),x2(t))dt+

式中：LV(x1(t),x2(t))如式(15)所示. 这样

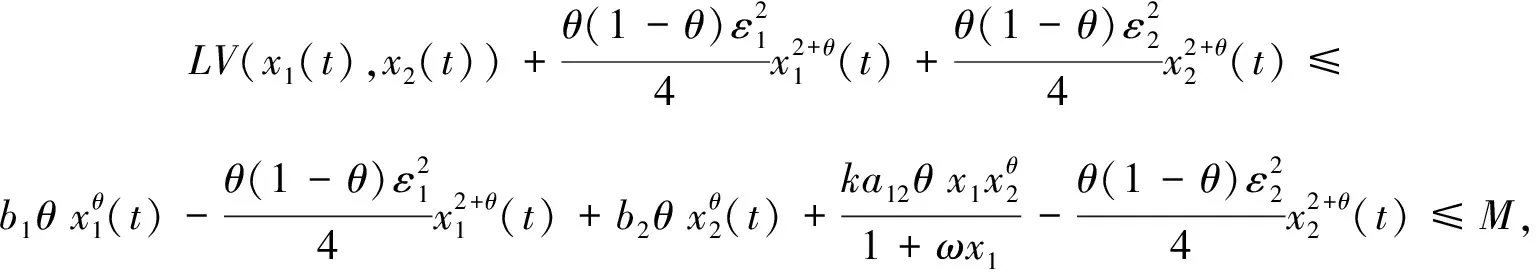
将式(20)代入式(18)中, 有

即

两边从0到τn∧T取积分并求期望, 得

即

两边同除以T, 得

4 结 论

捕食系统的研究具有一定的理论和应用价值. 考虑到环境噪音的普遍存在性, 随机白噪音捕食系统得以建立. 本文对具时滞和 Holling-type Ⅱ 功能反应的捕食随机系统进行研究, 讨论了系统的一些性质, 其中包括全局正解的存在唯一性与解的随机最终有界性, 同时对解的渐近矩进行了估计. 这些性质为种群动力系统的管理提供了理论依据. 基于这些工作基础, 我们还可以研究具有其他类型功能反应的种群动力学系统.

[1] 王克. 随机生物数学模型 [M]. 北京： 科学出版社, 2010.

[2] Zhou J. Positive steady state solutions of a Leslie-Gower predator-prey model with Holling type Ⅱ functional response and density-dependent diffusion[J]. Nonlinear Analysis, 2013, 82(1)： 47-65.

[3] Hong K, Weng P X. Stability and traveling waves of a stage-structured predator-prey model with Holling type-II functional response and harvesting[J]. Nonlinear Analysis： Real World Applications, 2013, 14(1)： 83-103.

[4] Zhu Y L, Wang K. Existence and global attractivity of positive periodic solutions for a predator-prey model with modified Leslie-Gower Holling-type Ⅱ schemes[J]. Journal of Mathematical Analysis and Applications, 2011, 384(2)： 400-408.

[5] Aziz-Alaoui M A, Daher Okiye M. Boundedness and global stability for a predator-prey model with modified Leslie-Gower and Holling-type Ⅱ schemes[J]. Applied Mathematical Letters, 2003, 16(3)： 1069-1075.

[6] Li Y Q, Gao H L. Existence, uniqueness and global asymptotic stability of positive solutions of a predator-prey system with Holling Ⅱ functional response with random perturbation[J]. Nonlinear Analysis, 2008, 68(6)： 1694-1705.

[7] Ji C Y, Jiang D Q, Shi N Z. Analysis of a predator-prey model with modified Leslie-Gower and Holling-type Ⅱ schemes with stochastic perturbation[J]. Journal of Mathematical Analysis and Applications, 2009, 359(2)： 482-498.

[8] Ji C Y, Jiang D Q, Shi N Z. A note on a predator-prey model with modified Leslie-Gower and Holling-type Ⅱ schemes with stochastic perturbation[J]. Journal of Mathematical Analysis and Applications, 2011, 377(1)： 435-440.

[9] Liu Q, Chen Q M. Asymptotic behavior of a stochastic non-autonomous predator-prey system with jumps[J]. Applied mathematics and Computation, 2015, 271(15)： 418-428.

[10] Lü J L, Wang K. Asymptotic properties of a stochastic predator-prey system with Holling Ⅱ functional response[J]. Communications in Nonlinear Science and Numerical Simulation, 2011, 16(10)： 4037-4048.

[11] Jiang D Q, Shi N Z, Li X Y. Global stability and stochastic permanence of a non-autonomous logistic equation with random perturbation[J]. Journal of Mathematical Analysis and Applications, 2008, 340(1)： 588-597.

[12] Kuang Y. Delay differential equations with applications in population dynamics[M]. New York： Academic, 1993.

[13] Fan Y H, Li W T. Permanence for a delayed discrete ratio-dependent predator-prey system with Holiing type functional response[J]. Journal of Mathematical Analysis and Applications, 2004, 299(2)： 357-374.

[14] Liu G R, Yan J R. Positive periodic solutions for a neutral delay ratio-dependent predator-prey model with a Holling-type Ⅱ functonal response[J]. Nonlinear Analysis： Real World Applications, 2011, 12(6)： 3252-3260.

[15] Mao X R. Exponential stability of stochastic differential equations[M]. New York： Dekker, 1994.

[16] Bahar Arifah, Mao X R. Stochastic delay Lotka-Volterra model[J]. Journal of Mathematical Analysis and Applications, 2004, 292(2)： 364-380.