带有自愿接种博弈的SIV性传染病模型的建立与分析

汤瑞瑞， 张菊平

(中北大学 理学院， 山西 太原 030051)

0 引 言

性传染病(Sexually-Transmitted-Disease, STD)是指经性接触传播疾病的统称， 由于传播速度快， 影响范围广， 已成为常见的公共卫生问题之一[1,2]. 目前， STD在普通人群中的患病率为0.067%， 而STD高危人群的患病率为5%～62.8%[2]， 因此， 研究STD高危人群对疾病的传播与控制具有重要意义[2-5].

近年来， 疫苗作为有效控制策略之一， 被广泛用于减少STD的传播[6]. 已有的理论模型常考虑疫苗接种的“成本”， 既考虑疫苗接种成本也考虑副作用[6-10]， 而个体根据疫苗的“成本-效益”来决定否接种[9,10]. 文献[6]中建立了带有自愿接种免疫博弈的STD传播模型；文献[8]中用马尔科夫随机过程和博弈论评估个体利益和群体之间的博弈， 并将其应用到一类简单疫苗接种博弈中；文献[10] 建立了一类非线性传染病模型， 并利用光滑反映函数描述模型中易感人群如何在面临被感染危险、 接种收益和接种风险在内的接种总体成本之间博弈.

本文结合实际情况， 将STD中的易感人群分为高危人群与低危人群， 建立了针对高危人群带有自愿接种博弈的SIV性传染病传播动力学模型， 并给出了基本再生数， 分析了平衡点的存在性与稳定性.

1 带有自愿免疫博弈的SIV模型

1.1 SIV模型的建立

将总人口N(t)分为四类: 高危易感者、 低危易感者、 染病者和免疫者， 分别用Sh(t)，Sl(t)，I(t) 和V(t)表示t时刻这四类人群的人口数， 则N(t)=Sh(t)+Sl(t)+I(t)+V(t). 假设新进入者都是低危易感者， 用Λ表示. 疾病的传播过程如图 1 所示.

图 1 疾病传播流程图Fig.1 Flow chart of disease transmission

图 1 中a表示自然死亡率系数；f表示免疫接种率系数；u表示免疫失效率系数；m1表示高危易感者向低危易感者的转换率系数；m2表示低危易感者向高危易感者的转换率系数；βh表示高危易感者每次接触传染的概率；βl表示低危易感者每次接触传染的概率；b表示因病死亡率系数. 以上参数都是非负的. 根据流程图 1， 可以建立动力学方程

(1)

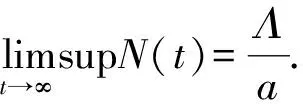
系统的可行域为

1.2 自愿免疫的博弈

个体接种疫苗不仅可产生抗体， 抵抗疾病， 即为接种的效益， 同时需要承担接种疫苗实际支付的货币及疫苗的副作用， 即接种的“成本”， 故个体接种的决策依赖于接种的“成本”与效益. 如果个体能够自己决定是否接种， 则可以用博弈论来描述个体接种决策的理性行为. 当疫苗的“成本”高于其效益时， 个体作出避免接种的理性决策；反之， 个体做出接种的决策. 用Δω表示效益与“成本”的差值， 即总效益.

首先考虑接种的效益， 当疾病传染率较大时， 易感个体接种疫苗会有较大的获利， 即个体接种的效益与被传染的概率βhI成正相关. 同时， 接种的效益也依赖于染病者的痛苦程度及STD因病死亡率. 染病者的痛苦程度越大， 个体接种的效益越大；因病死亡率越大， 疫苗接种预期效益就越大. 用p表示个体预期的与疾病相关的痛苦，ε表示染病者对因病死亡的恐惧(意识). 因此， 易感者预期接种的效益可表示为βhI(bε+p). 其次， 个体接种疫苗需要承担疫苗的“成本”， 用c表示， 则个体预期接种疫苗的总效益为

Δω=βhI(bε+p)-c.(2)

基于实际情形考虑， 当Δω<0时， 个体做出避免接种的决策， 此时个体选择接种的概率较小， 且Δω→-∞时接种率几乎为0；当Δω=0时， 个体有一半的概率做出接种的决策；当Δω>0时， 个体做出接种的决策， 且Δω→+∞时接种率几乎为1. 个体接种疫苗的概率随着Δω的增加而增加， 故采用Logistic方程来描述个体自愿接种免疫的理性决策， 即

(3)

2 SIV模型的分析

2.1 无病平衡点和基本再生数的关系

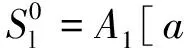
V0=A1φm2,

这里

根据基本再生数的定义， 得

βl[aφ+(1+erc)(m1+a)(μ+a)]].

定理1 当R0<1时， 无病平衡点E0是局部渐近稳定；当R0>1时，E0不稳定.

证明系统(1)在无病平衡点E0处的雅克比矩阵为

(5)

雅克比矩阵JE0所对应的特征方程为

λ(μ+2a+m1+m2+f0)+(μ+a)(m1+

m2+a)+(m2+a)f0]=0.(6)

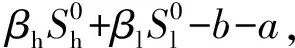
λ2+λ(μ+2a+m1+m2+f0)+

(μ+a)(m1+m2+a)+(m2+a)f0=0.(7)

由方程(7)的判别式及根和系数的关系得方程有两个负的实根. 因此， 若使所有特征根均为负， 当且仅当特征根λ2<0即可， 而λ2<0⟺R0<1，λ2>0⟺R0>1.

综上， 当R0<1时， 无病平衡点E0局部渐近稳定；当R0>1时，E0不稳定.

2.2 正平衡点的存在性及稳定性

下面求解系统(1)的正平衡点.

而x满足方程

a1x2ex+a2xex+a3ex+a4x2+a5x+a6=0,(8)

这里

a2=βlΛβh(μ+a)-aβlφ(b+a)-

(μ+a)(b+a)(aβl+aβh+βhm2+βlm1),

a3=r(bε+p)[aφβh(βlΛ-(b+a)(a+m2))+

Λβh(μ+a)(m2βh+m1βl+aβl)-

aβh(μ+a)(b+a)(a+m1+m2)],

a4=a1erc,

a5=a2erc+aφβl(b+a)erc,

a6=a3erc+aφβhr(bε+p)erc[(b+

a)(a+m2)-Λβl].(9)

由式(8)和式(9)整理可得，x满足

a1x2+a2x+a3=

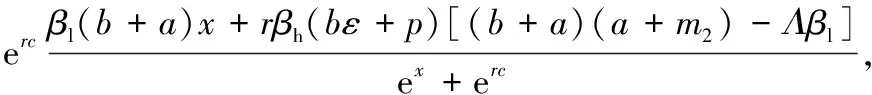
即x是方程(11)与方程(12)的交点

y1(x)=a1x2+a2x+a3,(11)

y2(x)=

当R0=1时， 有y1(0)=y2(0)， 此时该平衡点为无病平衡点.

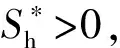
下面判断在系统(1)的可行域内函数y1(x)与y2(x)是否存在交点. 首先给出它们各自的导函数， 为

(13)

其中,A=-aφercβl(b+a),B=-aφercrβh(bε+p)[(b+a)(a+m2)-Λβl].

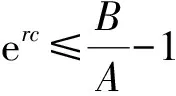
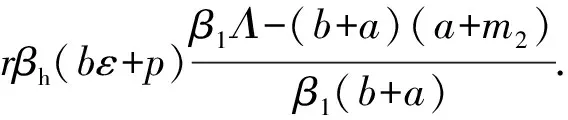
综上， 当R0>1时， 系统(1)存在正平衡点E1.

3 数值模拟

首先确定模型的参数， 如表 1 所示. 对于Λ， 2016年以前中国每年新增人口数相对稳定， 自2016年1月 1日开放二胎政策以来中国每年新增人口数变动比较大， 故以2016年以前的中国每年新增人口数为低危易感者数量.

表 1 模型中参数的取值范围

考虑系统(1)中博弈参数对各个变量的影响. 图 2 表示是系统(1)中Sh，I，V随c的变化情况. 随着c的增加， 个体接种成本增加， 基于博弈理论的“成本-效益”分析， 个体选择接种的概率降低. 因此， 染病者的数量应该增加. 但是， 图 2 显示当c较小时， 随着c的增加高危人群和染病者的数量逐渐减小， 接种者的数量反而增加. 因为由接种率系数f可知， 当c→0时，f主要随I的变化而变化， 而在c→0时染病者的数量相对较大. 也就是说， 当疾病流行规模较大时， 个体对于接种缺乏理性的判断， 这与我们的实际情况相吻合. 当染病者的数量降到最低点之后， 随着c的增加， 染病者的数量也逐渐增加， 此时个体对于疫苗接种遵循“成本-效益”博弈. 综上， 个体对于疫苗接种的理性决策与疾病传播规模以及疫苗接种“成本”有关， 这两类信息在疾病流行规模较大时产生相反的效果. 同时由图 2(a) 和(b) 可知STD中的高危人群对疾病的传播与控制起决定性作用.

图 2 c对Sh ，I，V的影响关系图Fig.2 Curves of effects of c on Sh，I，V

为了了解最大免疫率系数φ及个体对成本差异的敏感性r对疾病传播的影响， 分别做了2幅模拟图， 如图 3 所示.

图3(a)显示，I随着最大免疫率系数的增加基本保持不变， 表明了仅增强高危人群的接种预防意识不足以降低疾病的传播；Sh随着最大免疫率系数的增加呈下降趋势，V随着最大免疫率系数的增加呈上升趋势， 表明增强高危人群的接种预防意识可降低疾病潜在的爆发风险. 图3(b)显示了个体对成本差异的敏感性r对疾病传播的影响. 可知当个体对成本差异不敏感时， 接种者对于疫苗的“成本-效益”的估计不准确； 反之， 个体对成本差异越敏感， 接种者对于疫苗的“成本-效益”的估计就越准确. 由图3(b) 可知,Sh随着个体对成本差异敏感性的增加呈上升趋势，V随着个体对成本差异敏感性的增加呈下降趋势， 表明当高危人群对于疫苗“成本-效益”的估计变得准确时， 隐藏着较大的疾病爆发风险. 也就是说,当个体了解大量的疫情信息时反而不利于疾病的控制.

图 3 φ,r分别对Sh，I，V的影响关系图Fig.3 Curves of influence of φ,r on Sh,I,V respectively

4 结 论

本文主要讨论了性传染病高危人群自愿接种博弈的ShSlIV传染病模型. 首先， 采用Logistic方程给出了带有博弈的接种率系数；其次， 理论分析了无病平衡点和正平衡点的存在性， 并证明了R0<1时无病平衡点E0呈局部渐近稳定性.

实验结果显示， 个体对于STD接种的理性决策基于STD蔓延速度及疫苗的“成本”， 这两类信息在STD蔓延较快时产生相反的效果， 不同于文献中所得出的结论. 因此政府机构可以根据STD的流行规模(或高危人群的流行规模)及疫苗的“成本”来采取有效控制STD流行的策略. 当高危人群对于疫苗的成本和效益的估计变得更准确(或更敏感)或对疾病预防意识较弱时， 此时隐藏着较大的疾病爆发风险， 这在文献中没有说明. 最重要的是， 对于疫情传播信息的扩散， 政府应该有一个合理的调控， 因为对于一般的个体， 了解过多的STD疫情信息反而不利于STD的控制.

[1] 叶顺章. 性传播疾病的实验室诊断[M]. 北京： 科学出版社， 2009.

[2] 叶顺章， 邵长根. 性病诊疗与预防[M]. 北京:人民卫生出版， 2002.

[3] 马迪辉， 张彦琦， 周亮， 等. 重庆市2006-2012年艾滋病高危人群HIV/AIDS流行情况分析[J]. 第三军医大学学报， 2015， 37(7)： 689-692.

Ma Dihui， Zhang Yanqi， Zhou Liang， et al. Epidemiological analysis of HIV/AIDS prevalence among high risk population of AIDS in Chongqing during 2006-2012[J]. Journal of the Third Military Medical University， 2015， 37(7)： 689-692. (in Chinese)

[4] 黄晓梅. 荆门市2015年艾滋病哨点监测工作报告[J]. 中国卫生产业， 2015(19)： 188-190.

Huang Xiaomei. Report on sentinel surveillance of AIDS in Jing Men in 2015[J]. China Health Industry， 2015(19)： 188-190. (in Chinese)

[5] 吴文其， 熊云新， 覃远生， 等. 高危人群性传播疾病流行情况[J]. 中国热带医学， 2007， 7(1)： 122-123.

Wu Wenqi， Xiong Yunxin， Tan Yuansheng， et al. Prevalence of sexually transmitted diseases among high-risk groups[J]. Chinese Journal of Tropical Medicine， 2007， 7(1)： 122-123. (in Chinese)

[6] Xu F， Cressman R. Voluntary vaccination strategy and the spread of sexually transmitted diseases[J]. Mathematical Biosciences， 2016， 274： 94-107.

[7] Shim E， Albert S M， Burke D S， et al. A game dynamic model for vaccine skeptics and vaccine believers： measles as an example[J]. Journal of Theoretical Biology， 2011， 295(295)： 194-203.

[8] Reluga T C， Galvani A P. A general approach for population games with application to vaccination[J]. Mathematical Biosciences， 2011， 230(2)： 67-78.

[9] Schimit P H T， Monteiro L H A. A vaccination game based on public health actions and personal decisions[J]. Ecological Modelling， 2011， 222(9)： 1651-1655.

[10] Xu F， Cressman R. Disease control through voluntary vaccination decisions based on the smoothed best response[J]. Computational & Mathematical Methods in Medicine， 2014， 2014(6)： 825734.

[11] 中华人民共和国国家统计局. 中国统计年鉴[EB/OL]. 2017-01-05. http:∥www.stats.gov.cn/tjsj/ndsj/.html.