浅谈初中数学信息型试题的解题策略

张斌

摘 要 信息题是初中数学的常见题型，这类试题形式多变，能够将实际场景的问题以图像、表格及一定的文字说明的形式呈现，增加试题的灵活性和趣味性。本文试着列举典型例题进行分析和总结，以给同学们一些启示。

关键词 初中数学;信息型试题;解题

中图分类号：G632 文献标识码：A 文章编号：1002-7661（2018）15-0186-02

信息题是一种通过图表、表格以及一定的文字来描述题目情景的题型，又可以称为图表信息题。通过分析解答信息题，能够提高学生收集有效信息、分析试题以及解决试题的能力。信息题常见有三种类型：图像类信息题、表格类信息题以及情景类信息题，本文将对这三种题型进行举例分析，讲解解题技巧，以便给同学们一些启示。

一、图像类信息题

此类问题是将已知条件以图像的形式给出。这类问题需要仔细观察题目中所给的图像，分析图像，理解图像上各图形所代表的含义，从而结合图像解决实际问题。

例1 某市保险公司推出一种针对农民医疗费报销的商业险，购买此保险后，村民只要每人每年交10元钱就可以，每年先由自己支付医疗费，年终时可得到按一定比例返回的返回款，这一商业险的推出大幅度的增加了农民抵御大病风险的能力。李磊与同学们都某一地域的农民进行了随机抽查，并将收集到的信息绘制成以下图形。

请依照上述内容，回下下列问题：

（1）李磊的这次抽查活动中，共有多少多少村民参加到此次活动中;在接受抽查的村民中，有多少人得到了商业险承诺的返回款;

（2）假设该地域有10000村民居住，请估计下有多少村民购买了此项商业险？若保险公司期望在两年之后将购买商业险的人数增加到9680人次，在假设这两年人数增长率相同的情况下，求解这个人数增长率为多少。

分析：（1）根据样本容量为各族频数之和，可得共有240+60=300（人）;其中有2.5%即6人得到了返回款;

（2）用样本估计总体即可得出答案。

解：（1）调查的村民数=240+30=300人，购买商业险得到了返回款的人数=240×2.5%=6人;

（2）∵购买商业险的人数百分率为240/300=80%，

∴估计该乡购买商业险的村民有10000×80%=8000人，

设年增长率为X，由题意知8000×（1+X）2=9680，解得：X₁=0.1，X₂=2.1（舍去），即年增长率为10%。

答：共调查了300人，得到返回款的村民有6人，估计有8000人参加了合作医疗，年增长率为10%。

二、表格类信息题

表格类信息题通常用表格列举出已知条件，此类问题的解题关键是正确分析表格中的数据，提取有效的信息搞清楚数据间的相互关系，具体分析如下：

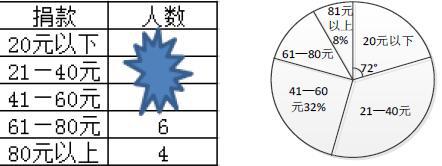
例2某校初三（1）班的同学踊跃为“雅安芦山地战”捐款，根据捐款情况（捐款数为正数）制作以下统计图表，但生活委员不小心把墨水滴在统计表上，部分数据看不清楚。

（1）全班有多少人捐款？

（2）如果捐款20元以下的人数在扇形统计图中所占的圆心角为72°，那么捐款21-40元的有多少人？

解：（1）4÷8%=50

答：全班有50人捐款。

（2）方法1：

∵捐款0-20元的人數在扇形统计图中所占的圆心角为72°

∴捐款0-20元的人数为50×72/360=10

∴50-10-50×32%-6-4=14

答：捐款21-40元的有14人。

方法2：

∵捐款0-20元的人数在扇形统计图中所占的圆心角为72°

∴捐款0-20元的百分比为72/360=1/5=20%

∴50×（1-20%-32%-6÷50-8%）=14

答：捐款21-40元的有14人。

三、情景类信息题

情景类信息题就是将试题中的有效信息以文字的形式表述出来，但并不是所有给出的条件都是有效信息，因此这类题型能够锻炼学生对信息的筛选、分析和归纳能力。学生需要分析出混杂在已知条件中的有效信息，确认试题的考点，采用正确的知识点进行解答。

例3：某渔场计划购买A、B两种小鱼苗，总共购买6000尾，A种鱼苗每尾0.5元，B种鱼苗每尾0.8元。相关资料表明：A种鱼苗的存活率为90%，B种鱼苗的存活率为95%。

（1）假设购买A、B两种鱼苗6000尾，总共花费了3600元，请问购买A种鱼苗多少尾，B种鱼苗多少尾。

（2）假设该渔场预计最多花费4200元来购买A、B两种鱼苗，那么A、B两种鱼苗又分别要购买多少尾？

（3）该渔场预计将这批鱼苗的存活率控制在93%以上，并且将费用控制在最低，那么A、B两种鱼苗又分别要购买多少尾？

解：（1）设购买A种鱼苗X尾，那么购买B种鱼苗（6000-X）尾，

由题可知：0.5X+0.8（6000-X）=3600，

解这个方程，得：X=4000，

∴6000-X=2000

答：A种鱼苗共买4000尾，B种鱼苗共买2000尾。

（2）由题可知：0.5X+0.8（6000-X）≤4200，

得：X≥2000，

即购买A种鱼苗不应少于2000尾，B不超过4000尾。

（3）设购买鱼苗的总费用为y，A种鱼苗买了X尾。

则y=0.5X+0.8（6000-X）+0.3X+4800，

由题意，有90/100×95/100（6000-X）≥93/100×6000，

解得X≤2400，

在y=0.3X+4800中，

∵0.3X<0，∴y随X的增大而减少，

∴当X=2400时，y_最小=4080。

答：购买A种鱼苗2400尾，B种鱼苗3600尾时，总费用最低。

四、结语

初中数学考试中，通过解答信息题能够锻炼学生对信息的筛选和分析处理能力。解决信息题的关键，在于将题目中所给出的图、表以及文字信息吃透，分析出题目的考点所在，将信息与对应的数学知识点相结合，发挥学生的联想能力，正确的运用数学公式解决题目。

参考文献：

[1]解玉华.浅谈初中数学解题技巧[J].数理化解题研究，2017（26）：18.

[2]李秀琴.浅析初中数学应用题解题技巧的探讨[J].中外交流，2017（15）.

[3]朱国京.浅谈初中数学解题策略实践方法[J].读书文摘，2017（8）.

[4]李新茹.浅析初中数学解题策略实践应用研究[J].数学大世界（上旬），2016（7）.

[5]代影.浅析初中数学的解题方法与技巧[J].数理化解题研究，2016（35）：23.