基于迭代重加权的高阶张量图匹配算法
徐国夏, 韩立新, 石冰,2
(1.河海大学 计算机与信息学院, 南京 211100; 2.安庆师范大学 计算机与信息学院, 安庆 246000)
0 引言
图匹配问题在计算机视觉和模式识别中是一个非常基础且重要的问题。图匹配作为图像相似性度量的一种方法,多用于图像分析处理等任务。例如遥感图像融合处理、医学图像处理,航空影像自动制图等方面。在诸多应用驱动下产生了一系列实际场景,例如图像检索[1]、形状匹配[2]、目标追踪[3]等。图匹配基于图模型描述图像特征,通过节点和边来表示图像特征元素和图像特征元素之间的关系。这是对图像从像素级特征表示到高级语义级特征表示的拓展,具有表示复杂视觉模式的能力。近年来,研究工作者逐渐开始关注高阶图匹配,其利用张量的结构表示特征点集间的高阶图结构关系,能更好地解决图像特征表示与建模的歧义性问题。高阶图匹配[7]利用超图(Hyper-graph)来对应构建视觉特征集之间的关系,超图是3个特征点或者是3个以上特征点集对之间的关系。
从优化角度来说,图匹配问题其本质上是一种离散组合优化问题,其本身具有NP(non-deterministic polynomial) hard性质。因此大多数图匹配的解决方案是从优化角度出发寻找有效的近似算法[4],首先对匹配问题的离散约束进行一定程度上的松弛,再对松弛后的问题利用优化方法进行求解。图匹配方法中比较有代表性的方法有:基于谱方法,Leordanu等[5]提出了谱匹配SM(Spectral Matching)方法。 基于双随机约束松弛方法,Zaslavskiy等[6]基于凹凸松弛提出了一种(path-following)的方法,将图匹配问题松弛成了目标函数的凸和凹松弛问题。但是基于谱方法和双随机约束松弛的方法忽视了匹配问题的离散约束性,故越来越多基于稀疏约束的匹配方法增加稀疏约束来获得更有效的稀疏优化解。
Duchenne等[7]将高阶图匹配TM(Tensor Matching)问题形式化成一个三阶张量的目标函数,结合L1范数并得到匹配的稀疏解。文献[9]证明了L1/2范数其具有无偏性、稀疏性等良好的理论性质,其在变量选择和特征提取上的表现优于L1范数和L2范数。为进一步探索稀疏优化技术在图匹配中的应用,本文将高阶张量图匹配模型与L1/2范数结合,通过迭代重加权的优化方式近似求解该正则子,提出了基于L1/2范数重加权改进的高阶图匹配算法(Iterative Reweight High-order Graph Matching, IRHGM),力求在所构建的非凸非光滑的模型上取得最优的解稀疏性和噪声鲁棒性。实验证明本文的算法比传统方法具有更高的匹配正确率及更强的鲁棒性。
1 原理背景
1.1 基于张量高阶图匹配模型
基于张量的高阶图匹配算法在二阶谱匹配的基础上拓展而来,从点对点(point-to-point)、线对线(line-to-line)拓展到三角结构到三角结构(triple-to-triple)。拓展的不仅仅是比较的数量级,更多的是在模型上从原来的线性向非线性的推广。利用三阶张量结构信息更能覆盖目标特征点之间的多重几何组合关系,对噪声、尺度不变性、仿射不变性、分辨率、视角变化等的干扰具有更强的鲁棒性。张量(tensor)[8]是多维矩阵的拓展,张量可以由诸多基于若干个坐标系中发生转换关系改变的集合分量定义。N阶张量表示为A∈RL1×L2×…×LN,A中的元素表示为xl1l2…ln。与矩阵的Frobenius范数类似,张量的F范数可以表示成式(1)。
(1)
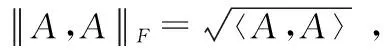
高阶图匹配中利用高阶图结构信息来构建关系张量A,首先在特征点集中选取(i,j,k) 三个点,组成一个点集元组,该元组相似度量值由其组成的三角形结构信息fi,j,k,和另一个相对应元组fi′,j′,k′来度量为式(2)。

(2)
关系张量A是一个超对称的张量,以稀疏存储的方式存储坐标及相对应度量值。基于张量表示的高阶图匹配模型能够自然地对高阶结构内在的几何结构和关联关系进行描述,解决了图像特征表示的结构化建模。
基于候选匹配进行矩阵约束可以将其划分成一个二次分配问题,该目标函数通过对关系矩阵的行列约束得到最优匹配结果为式(3)。
(3)
高阶图匹配问题是在矩阵基础上推广成高阶张量表达,定义了与张量有关的目标函数为式(4)。
(4)
在两组点集中{P}和{Q},其点集中特征点个数分别是p,q。该高阶匹配模型的目标是在点集中找到相对应的点集对关系,匹配解X是由0,1组成的分配矩阵。高阶匹配模型是在三组约束下,通过寻找相似三角形对来得到最优匹配结果。将分配矩阵X重新向量化为x=vec(X),大小为N=pq。模型(4)可以用tensor-vector乘法的定义为式(5)。
⊗ixi⊗jxj⊗kxk
(5)
⊗表示为Kronecker积的形式表达。
1.2L1/2范数
近些年发展起来的正则化方法在变量选择和特征提取等工作上得到广泛应用。如图1所示。
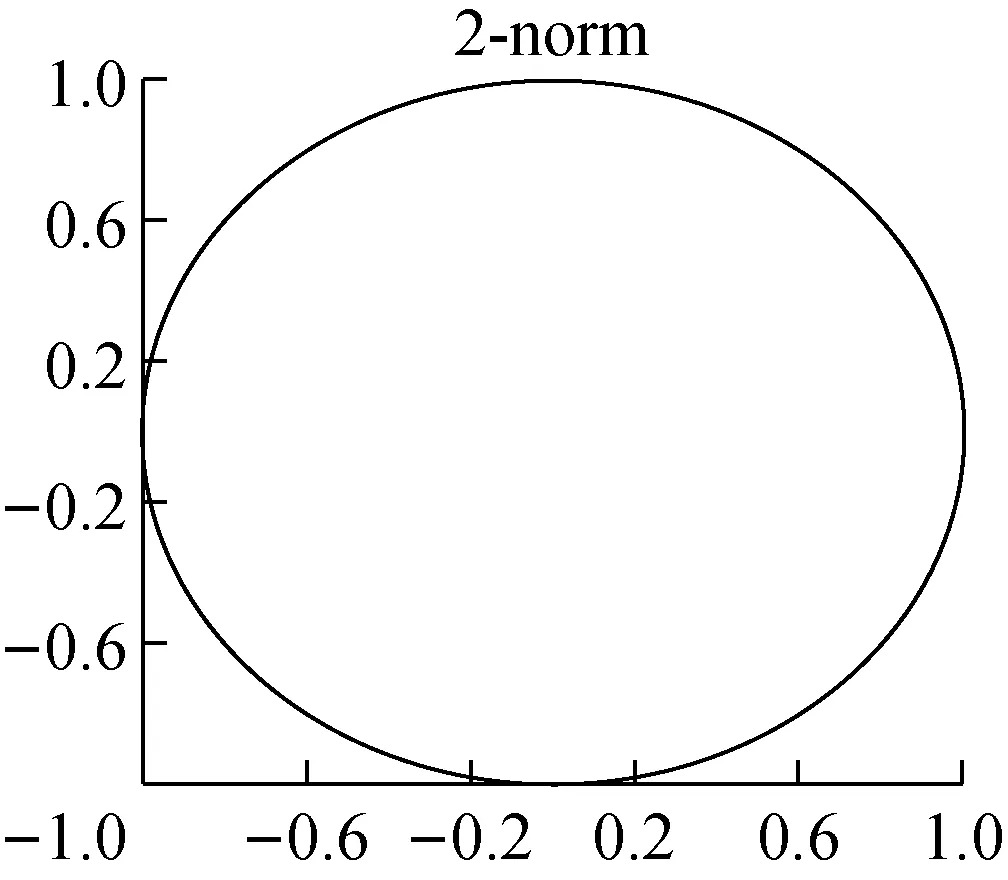
使用等距角度,将这些点投射在球上。使用标准图的连接线绘制排序点,以前在2-norm或者1-norm球上的等距点现在非常稀疏接近0.5-norm球。从直观的几何角度分析上来看,L1/2范数与L2、L1范数相比较曲线更加平缓,处在两者之下,更易于相交于等高线。因此L1/2范数的解会比其余两者更具稀疏性。
在诸多范数中,L0对应的是最优的变量选择结果,但是它本身就是一个NP问题。故一些工作已经证明L1已经在某种意义下是等价于L0的。L1/2范数是更具有应用价值的。Ochs等[10]研究将L1/2范数近似为重加权L1范数,更能产生稀疏的解。同时在求解L1/2范数的迭代算法问题上,利用已有的L1范数进行赋权求解。并且也证明了L1/2范数收敛性。
求解L1/2范数的算法流程如式(16)。
步骤1:初始化模型:
xt=(1,…,1)T,t=0
(6)
步骤2: 转化为模型:

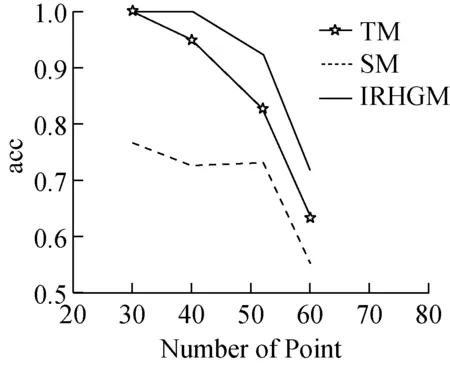
步骤3:当t s.t.∀x∈[0,1] (7) 模型(7)对分配矩阵X中的每个列分量xi进行约束,约束每一变量值在[0, 1]之间,λ控制模型复杂度。模型(7)是一个非凸非光滑的目标函数,相较于原始模型,通过L1/2范数控制解的稀疏性。同时本文也提出相对应的基于迭代重加权方法估计非光滑范数,将其近似为加权L1范数,如式(8)。 s.t.∀x∈[0,1] (8) 对于该模型的加权的L1范数,继续利用张量幂迭代进行推导。基于张量幂迭代的约束优化问题(8)的Lagrange函数定义为式(9)。 (9) (10) 算法1:基于迭代重加权的高阶图匹配算法(IRHGM) 输出:分配矩阵X 1) 初始化X={1,…,1}T 直到收敛 本文提出的基于L1/2范数的IRHGM算法,实验对象在House dataset标准数据集进行验证。本算法实验平台Intel(R) Xeon(R), 3.47GHz,CPU,Window7操作系统的PC,算法使用Matlab+Mex混合编程实现。本文提出的算法在下列3个方面均衡评价,对解集稀疏性,匹配准确率和抗噪鲁邦性进行实验比较。对比了基于L1范数张量匹配方法TM(Tensor Matching)[6]和基于L2范数谱匹配方法SM(Spectral Matching)[8]。 首先实验利用在准备实验数据点的时候,利用SIFT描述子提取候选备用点,分别提取30,40,50,60个实验节点。然后利用knn算法寻找出尽可能相似的三角形组合,分别可以寻找出630000,1120000,1892800,2520000个组合。在此基础上构建稀疏张量,这是一个非常大的稀疏张量,在这个张量空间中挖掘匹配结果。匹配准确率结果,如图2所示。 图2 不同实验节点个数下相应TM,SM, L1/2范数的高阶图匹配模型IRHGM的匹配准确率结果要优于其他算法。 分配矩阵X的稀疏性结果比较,如图3所示。 表明了IRHGM优于TM(基于L1范数)算法收敛得到的解,体现了本文提出算法的优越性。同时IRHGM稀疏性越高的基础也提高了匹配准确率。 本文同时在模型和优化方法上进行完善,该算法不仅考虑了解的稀疏保持性,同时更能抵抗匹配噪声,体现了算法的鲁棒性。在待匹配数据中增加了随机噪声,如图4所示。 图4中右边图片增加随机噪声点。不同实验节点再增加噪声点的实验对比,比较匹配准确率。可以看出IRHGM在整体准确率上优于其余算法,对存在噪声点的情况下仍然不会降低匹配准确率,如表1所示。 图3 本文提出的IRHGM匹配算法与TM匹配算法的解即对分配矩阵X的稀疏性结果比较图(IRHGM匹配正确率93%,TM匹配正确率83%,50个节点) L1/2norm L1 norm 图4 本文提出的IRHGM匹配算法和TM匹配算法结果示意图(连接线两端指向相同数字代表匹配正确,数字不相同和没有数字都代表没匹配上,且出现了一对多的误匹配)。 本文提出的算法IRHGM融合了高阶张量模型和更稀疏的L1/2范数稀疏约束,在保证全局优化基础上得到有效且稀疏的解,并且实验结果也验证了算法对于噪声的鲁棒性。 表1 在不同噪声点不同算法的准确率比较(%) 图匹配问题一直是计算机视觉中的基础问题,本文利用高阶张量超图模型和L1/2范数,提出了基于L1/2范数的迭代重加权高阶图匹配算法,以迭代重加权的方式近似求解赋权L1范数,优化高阶图匹配模型。实验证明本算法不仅得到了更优的解稀疏性,更增强了对匹配噪声的鲁棒性,与相关算法比,得到了更高的匹配准确率,能够更好的将匹配算法辅助运用到其他计算机视觉场景[12][13]中。未来我们考虑将稀疏约束引入多图匹配中的相关算法,进一步地提升多图匹配的匹配准确率。 [1] Helala M A E, Selim M M, Zayed H H. An Image Retrieval Approach Based on Composite Features and Graph Matching[C]. IEEE, International Conference on Computer and Electrical Engineering. 2009, pp:466-473. [2] Ngo, Quoc-Tao, Duc-Dung Nguyen, and Shu-Chuan Chu. Similarity Shape Based on Skeleton Graph Matching. [J] Journal Info. Multi. Signal Processing, 2016 7(6):1254-1264. [3] 王治丹, 蒋建国, 齐美彬. 基于最大池图匹配的形变目标跟踪方法[J]. 电子学报, 2017, 45(3):704-711. [4] 江波, 汤进, 罗斌. 计算机视觉中的图匹配方法研究综述[J]. 安徽大学学报(自科版), 2017, 41(1):29-36. [5] M. Leordeanu and M. Hebert. A spectral technique for correspondence problems using pairwise constraints [C]. IEEE International Conference on Computer Vision, Beijing, China, October, 2005, pp:1482-1489. [6] M. Zaslavskiy, F. Bach, and J. Vert. A path following algorithm for the graph matching problem [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2009, 31(12):2227-2242. [7] O. Duchenne, F. Bach, I.-S. Kweon, and J. Ponce. A tensor-based algorithm for high-order graph matching [J]. IEEE transactions on pattern analysis and machine intelligence, 2011, 33(12):2383-2395. [8] Papalexakis E E, Faloutsos C, Sidiropoulos N D. Tensors for Data Mining and Data Fusion: Models, Applications, and Scalable Algorithms[M]. ACM, 2016. [9] 张海, 王尧, 常象宇,和徐宗本. L_(1/2)正则化[J]. 中国科学:信息科学, vol.40, no.3, pp:412-420, 2010. [10] P. Ochs A. Dosovitskiy, T. Brox, and T. Pock. On Iteratively Reweighted Algorithms for Nonsmooth Nonconvex Optimization in Computer Vision [J]. Siam Journal on Imaging Sciences, 2015, 8(1):331-372. [11] Lathauwer L D, Moor B D, Vandewalle J. On the best rank-1 and rank-(R1, R2. . ,RN ) approximation of higher-order tensor[J]. Siam Journal on Matrix Analysis & Applications, 2000, 21(4):1324-1342. [12] Du D, Qi H, Li W, Huang Q and Lyu S. Online Deformable Object Tracking Based on Structure-Aware Hyper-Graph[J]. IEEE Transactions on Image Processing, 2016, 25(8):3572. [13] Dutta, Anjan, Josep Lladós, Horst Bunke, and Umapada Pal. Product Graph-based Higher Order Contextual Similarities for Inexact Subgraph Matching[OJ]. 2017. arXiv preprint arXiv:1702.003912 改进的基于L1/2范数的迭代重加权高阶张量图匹配模型

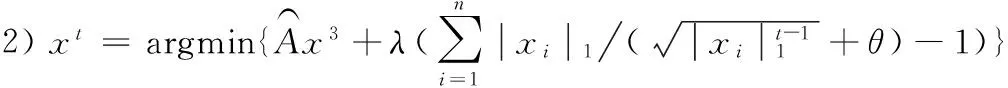

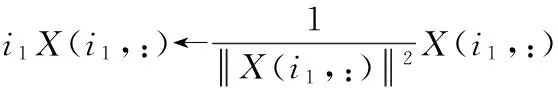
3 实验结果及分析





4 总结

