悬挂运动控制系统的设计与实现

张鹏， 何金保， 诸葛霞

(宁波工程学院 电信学院，宁波 315211)

0 引言

目前，随着科技的不断发展，运动控制技术已成为先进制造技术的关键技术，制造业采用机器换人的方式来实现工厂的运作，包括汽车的制造、食品的包装等无不采用自动化设备来完成机械的精准运动[1-4]。由于伺服系统具有精度高的特点，在运动控制系统中应用越来越广泛[5-6]。

本文悬挂运动控制系统以单片机为主要控制芯片，通过控制施加给电机驱动器的脉冲信号频率从而使电机按所指示的要求正转与反转已达到控制悬挂在吊绳上的物块精准移动的目的。本系统采用了数学上的微分思想，将复杂的画圆与画直线的过程分为简单且容易编程的走直线的方法，完成了一系列的定点、画直线、画圆的功能。通过一系列的程序调试以及器件的安装，最终在纸上得出了期望的图形。

1 系统方案

1.1 系统结构

本系统结构如图1所示。主要包括5个模块：控制器模块、红外寻迹模块、电机驱动模块、键盘模块、显示模块。控制器模块采用89C52单片机，电机驱动模块采用L297芯片，本系统用到2个电机，键盘模块采用阵列式键盘，显示模块采用液晶12864，红外寻迹模块是用来检测运动轨迹，是系统关键模块，检测精度直接关系到轨迹的准确性。

图1 系统组成结构图

本系统红外寻迹模块采用反射式红外探测器对坐标纸上的黑色线进行检测，原理上是根据黑色能够吸收大部分的可见光而白色会反射大部分的可见光。为了能够使红外探测器能够充分地完成寻迹功能，如图2所示。

图2 红外寻迹检测原理

在圆纸板的圆周上等间距地安装了8个红外发射接收对管，使它们围成一个半径为2 cm的圆周。我们使用的红外发射接受对管长约8 mm，所给黑线宽约2 cm，所以以这样圆周的方式安装传感器必定会有某个传感器检测到黑线。那么就控制单片机，让小圆纸板沿着能检测到黑色的那个红外探测器的方向去走。

把移动的方向分为以下的八种：其中1、3、5、7为四个主方向，哪个红外探测器检测到黑色信号时即往相应标号的方向前进。举例：当1和3两个方向的红外探测器同时检测到黑色信号，那么就往2号方向前进，直到信号消失为止。往各个方向的移动过程和上述微元思想一致，这里就不累赘了。

1.2 运动控制算法

1.2.1 点到点运动算法

物块的移动依赖于电机带动所悬挂的吊绳的移动。在我们的方案中，是将物块的坐标变化相应转化为吊绳长度的变化。假设初始的坐标值为(x1,y1)，所要移动到的点是(x2,y2),因为初始点是一开始手动已经定好了的，所以假设物块从初始点(x1,y1)到最终点(x2,y2)这一过程中，左电机移动的距离为a，右电机移动的距离为b，那么由上图3所示，在初始情况下根据勾股定理可得式(1)。

(1)

在移动到新位置(x2,y2)时，满足方程，如式(2)。

(2)

故得出的式(3)。

(3)

得出来的a与b的值即为电机所需转动相应的距离(转动的距离有单片机发出的脉冲信号决定)。由于a，b存在正负两种可能值，因而电机转动时也是相应的正转与反转，如图3所示。

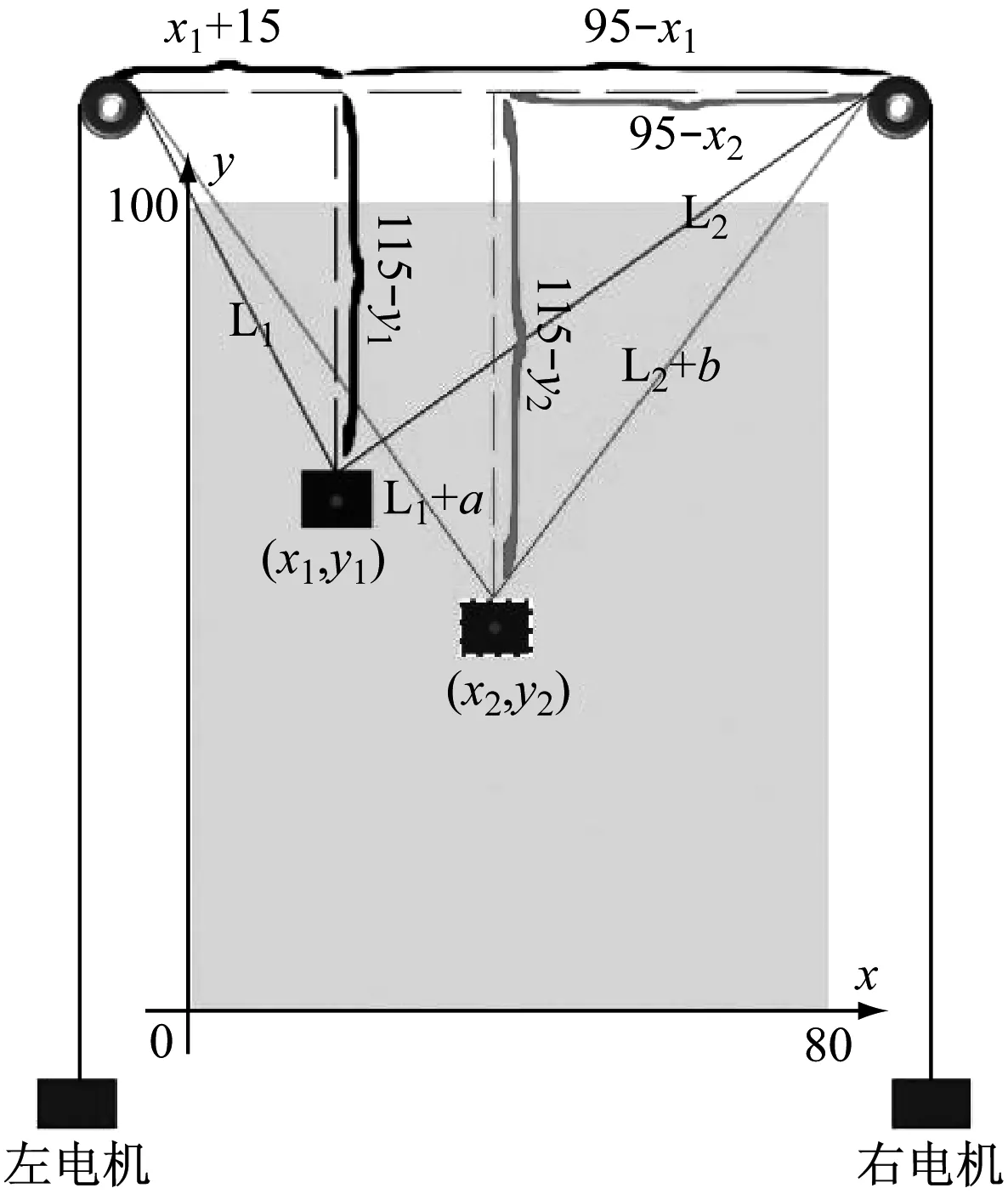
图3 点到点运动示意图

1.2.2 直线运动算法

从起始点(x1,y1)到终点(x2,y2)的物块定点移动中，假设每给一个脉冲，电机补给的线距为：m(该值可通过驱动上的细分调节)，那么选取t1=5*m(由于每给一个脉冲转动线距过小，因而稍稍加大细分长度)为每个水平细分的长度，t2=5*m*k为每个竖直细分的长度，如图4所示。

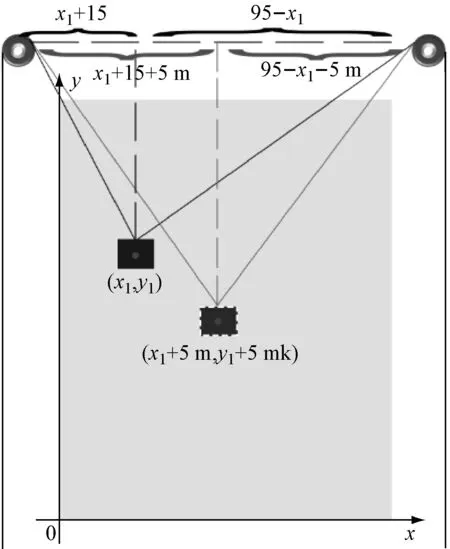
图4 直线运动算法示意图

t2中k的表达式为式(4)。

(4)

那么水平方向需要的计数次数为式(5)。

(5)

竖直方向需要计数次数为式(6)。

(6)

由图4，直线的方程为式(7)。

(1)

整理后得式(8)。

Tm=(x-x1)y-[(y2-y1)(x-x1)+y1(x2-x1)]

(2)

此时的每个细分长度电机所需转动的线距a,b可表示为(正负值对应相应的正反转)：

直线运动过程为：首先，物体由起始位置，向左平移一个单位(长度为5m)，得到一个新坐标(x1+5m,y1)。将该坐标值返回到单片机中带入直线方程(8)中的x与y，若Tm<0，则说明物块偏离在直线下方，开始进行+y方向上的数值位移5*m*k。若检测到Tm≥0时，则说明物块就在直线上或偏离在直线的下方，那么继续使物块水平移动，循环上述操作。直到Cntx与Cnty计数结束，完成画直线过程。

直线走向有如下的4种情况，如图5所示。利用1.2.1中定点的方法，根据每一种走向确定x与y的移动。

图5 直线运动4种情况

1.2.3 圆弧运动算法

画圆的过程依旧按照上述画直线那样的微元方法，将整个圆的曲线以无穷小的折线段来予以表示。当我们取得的折线段的长度越小时，所画出的圆更为精确。如图6所示。

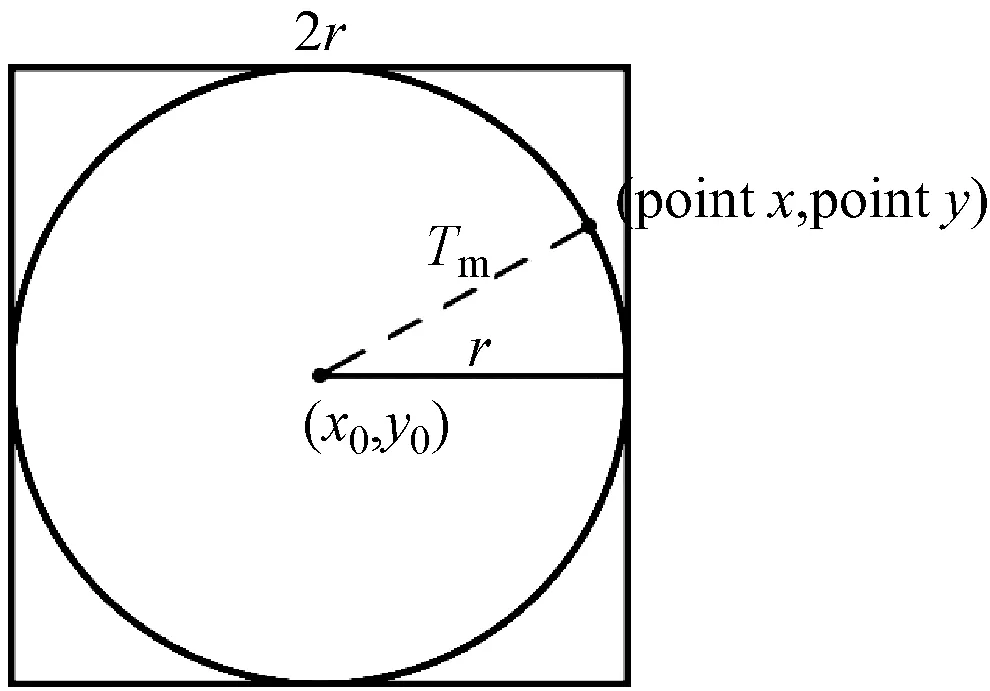
图6 圆弧示意图

假设所画圆的圆心坐标为(x0,y0),半径长度为r，那么该圆的方程为：

(x-x0)2-(y-y0)2=r2

画圆时，假设画笔的实时坐标为：(pointx,pointy)，那么可取判别式：

Tm=(pointx-x)2+(pointy-y)2

如若Tm≤r2，则认为画笔的当前位置是在圆内；而如若Tm≥r2，则认为画笔的当前位置是在圆外。

根据微元的思想，画笔横向运动与竖向运动的距离之和即为图6中该圆的外接正方形的周长，为8r。假设每给一个脉冲，电机补给的线距为：m(该值可通过驱动上的细分调节)。那么选取t1=2*m(由于每给一个脉冲转动线距过小，因而稍稍加大细分长度)为每个水平细分的长度，t2=2*m为每个竖直细分的长度。

为了逼近所画的圆，每次移动一个细分长度时都应该立即检测该点是否已经偏离所需要画的那个标准圆。如图7所示。

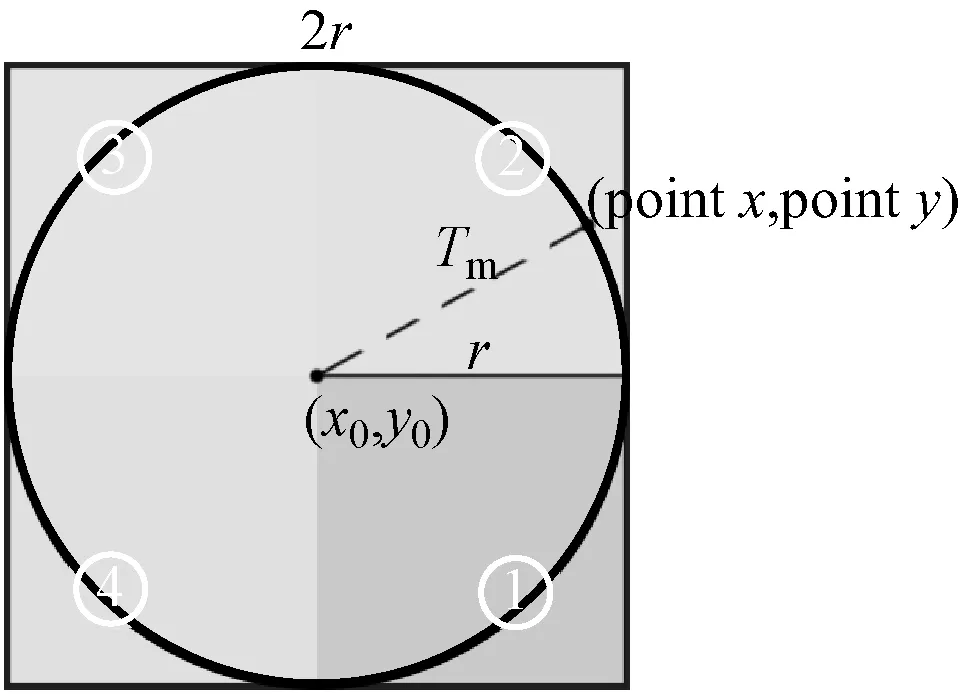
图7 圆弧运动算法

将图中区域分为如下①②③④4个部分：

分别讨论上述4种情况，如表1所示。表1中movex代表水平移动一个细分长度，movey代表竖直移动一个细分长度。正号代表正向移动，负号代表负向移动。且每一次移动时，计数次数加1。

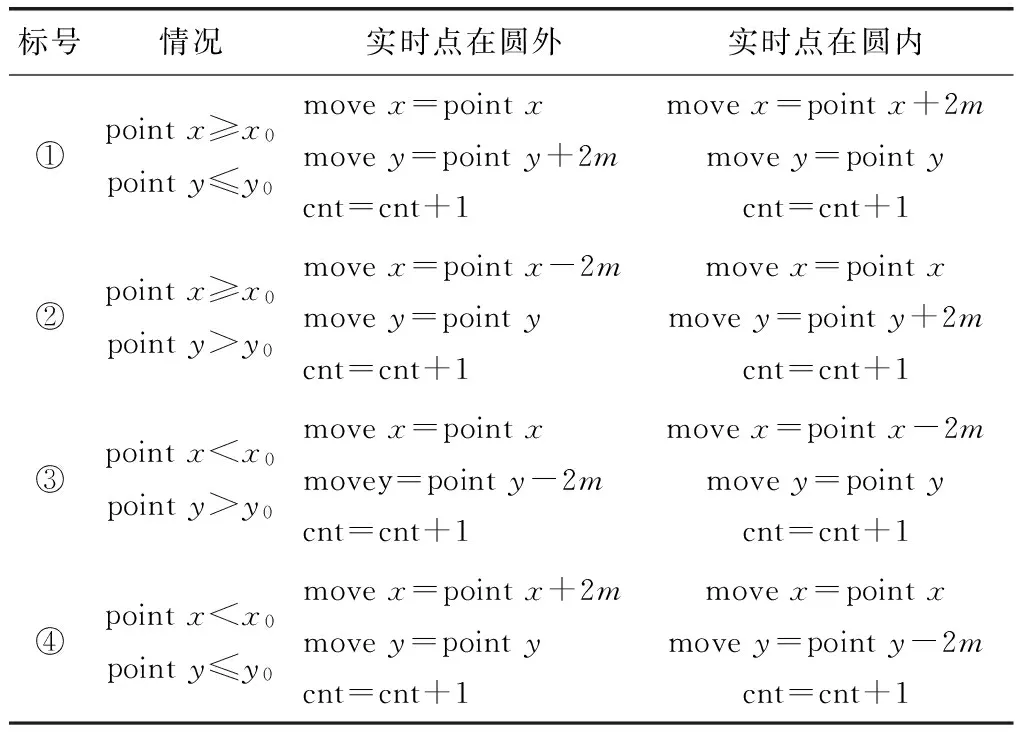
表1 圆弧算法四种情况

易知，总的计数次数为：

那么当实际计数次数Cntp≤Cnt时，画圆过程继续，当实际计数次数Cntp≤Cnt时，画圆过程完成。

1.2.5 模糊PID算法的精确控制

通过如上的算法，可以完成定点、走直线、画圆的功能。然而为了进一步地提高作图时的精确性，在实际中还引入模糊PID控制算法。当在画圆或者画直线的时候，画笔的实际位置与真实曲线偏差较大时才引入输出控制作用，使得电机的转速适当地增加到我们给定的速度值以使画笔能够更快地向理想的曲线靠拢。模糊PID可以根据运动控制中各独立运动轴所产生的轮廓误差大小及变化量实现PID控制参数实时优化，满足误差值以及误差变化率对PID三参数自整定在不同时刻的要求。将轮廓误差大小及变化量划分为负大、负小、零、正小、正大，建立Kp、Ki、Kd三者的参数值的大小模糊规则。通过模糊PID控制作用的引入，可以大大增加所作曲线的精度。

2 实验结果

直线和圆弧运动的PID和模糊PID控制效果比较，如表2和表3。

从实验的结果上来看，尽管存在微小的偏差，实验值与理论值也做到了基本吻合。且采用了模糊PID控制时所获得的曲线的精度更高。

3 总结

本文根据计划目标，完成了悬挂物的找点、画直线、画圆任务。在画直线与画圆的过程中，通过细分的方法用折线段近似地建构出了所要的图形，并且采用模糊PID算法，所画的图形与实际的图形误差较小，达到预期目标。

表2 直线运动的PID和模糊PID控制效果比较

表3 圆弧运动的PID和模糊PID控制效果比较

[1] 党智乾. 基于单片机的悬挂运动控制系统的设计与实现[J]. 计算机与数字工程, 2016, 45(07):1365-1370.

[2] 武林. 三维悬挂物体运动控制系统[J]. 浙江师范大学学报(自然科学版), 2007, 30(2):171-175.

[3] 吕弘, 赵佳. 悬挂运动控制系统的设计[J]. 伺服控制, 2014(4):49-51.

[4] 李小松, 马利业. 悬挂运动控制系统[J]. 兵器装备工程学报, 2010, 31(7):89-92.

[5] 江韦, 邹俊忠, 张见,等. 伺服运动控制轮廓误差补偿技术研究[J]. 制造技术与机床, 2016(4):73-78.

[6] 叶敦范, 刘金全, 欧阳才. 一种悬挂运动控制系统的近似插补算法研究[J]. 机械与电子, 2009(3):31-33.

[7] 张雨. 悬挂运动控制系统中误差补偿算法研究[D]. 吉林：吉林大学, 2012.