CBCT重建理论研究与改进

韩义波， 张枫， 靳冰

(南阳理工学院 软件学院,南阳 473000)

0 引言

影像技术一直是诊断疾病的重要手段，也是人们最早用于医学诊断的工程手段[1]。计算机断层成像(CT, Computed Tomography)技术能够在非接触、不破坏的情况下获得物体内部三维结构信息，目前已广泛应用于工业无损检测和医疗影像诊断等领域[2-4]。但大部分情况下我们得到的图像是二维数字断层图像序列，只能表达某一截面的解剖信息。因此，医生只能凭借经验，根据多幅二维图像估计病变部位的大小、立体几何形状及与周围组织之间的空间关系，这给诊断和治疗带来了不便。利用计算机图像处理、图形学、可视化技术和数学计算方法将二维断层图像序列转变成具有直观立体效果的图像的医学三维可视化技术，可以直观地展现三维立体结构空间关系，为辅助设计手术径路和模拟手术过程等提供可能。因此三维重建技术倍受人们的关注，得到了大量研究与广泛应用。

锥束CT(Cone-Beam Computed Tomography，CBCT)具有扫描速度快、空间分辨率高和射线利用率高的优点，已经越来越广泛地被使用[5]，它正成为CT研究的热点和发展方向[6]。三维锥束CT迭代重建算法是CBCT技术中较为关键的部分。图像重建技术包括两类基本方法：解析重建算法和迭代重建算法[7]。迭代算法可以重建各种扫描方式的图像，但具有计算量大、重建耗时较多的限制，解析重建算法由于其重建速度快，在图像重建领域中有着广泛应用。目前锥束CT图像重建广泛采用的解析型算法[8,9]。其中最著名的就是FDK (Feldkamp，Davis and Kress)算法[10]。由于是二维扇束算法的推广，它比基于三维 Radon变化的精确重建算法在数学上简单得多。而且，在锥角比较小的时候 (±4°间)，能够取得比较好的重建效果 ，有很好的商业应用前景[11]。近年来出现的多种近似算法都是基于这种算法发展而来的[11]。FDK 算法的优点是重建速度快，适合于完全投影数据及噪声水平较低情况下的重建。

2 理论基础

2.1 中心切片定理

中心切片定理，也叫投影切片定理和傅里叶中心切片定理，它是断层成像的理论基础。二维图像如图1所示。三维图像的中心切片定理如图2所示。分别如下描述。

定理1：二维函数f(x,y)的投影p(s)的傅里叶变换P(w)等于函数f(x,y)的傅里叶变换F(wx,wy)沿与探测器平行的方向过原点的片段。

图1 二维图像的中心切片定理

(a) 三维投影成像的中心切片定理

(b) 一组完整的测量数据

图1展示了二维图像的中心切片定理。如果探测器绕物体旋转180°，中心切片将布满整个傅里叶空间，我们就能得到完整的傅里叶变换函数F(wx,wy)，原本的图像f(x,y)就可以用反投影(Back-projection)和二维傅里叶反变换的数学手段获取。但仅靠反投影是无法得到原本图像的，为了消除模糊的效果，需要对傅里叶空间加权纠正，使其密度均匀，这个加权函数就是斜坡(Ramp)滤波器。如果是先滤波再做反投影的图像重建就叫做滤波反投影算法(FBP：filtered back-projection)。它的数学描述，如式(1)。

(1)

定理2：三维函数f(x,y,z)的投影的二维傅里叶变换P(wu,wv,θ)等于函数f(x,y,z)的三维傅里叶变换F(wx,wy,wz)沿与探测器平行的方向过原点的中心截面。其中，θ是u-v平面和wx-wy平面的法线方向。

图2(a)描述了三维成像的中心切片定理。如果θ的轨迹是单位球面上一个半径为1的圆圈，则可以保证傅里叶空间中每一个点上的值都能够被检测到。图2(b)展示了重建过程。

2.2 FDK算法

CBCT数据重建是一个朝气蓬勃的学科。但是，由于精确算法的数学复杂及计算量大，有许多理论结构简单的近似算法提出，其中最著名的就是FDK算法。FDK算法专门为锥形束的圆形焦点轨道而设计,它直接把二维的扇束重建算法推广到了三维锥束重建，从而提供一个近似的重建图像，比基于三维Radon变化的精确重建算法在数学上简单许多。而且，在锥角比较小的时候(±4°间)，能够取得比较好的重建效果。由于实用与稳定，它是目前CBCT图像重建最广泛采用的算法。

FDK算法主要包括3个步骤：加权、滤波和反投影。具体实现如下：

(1)对投影数据做加权运算：

(2)

其中，d为光源到旋转中心的距离，(u,v)为探测器平面坐标,pθ(u,v)是表示地θ角度的投影数据。FDK算法的几何坐标关系，如图3所示。

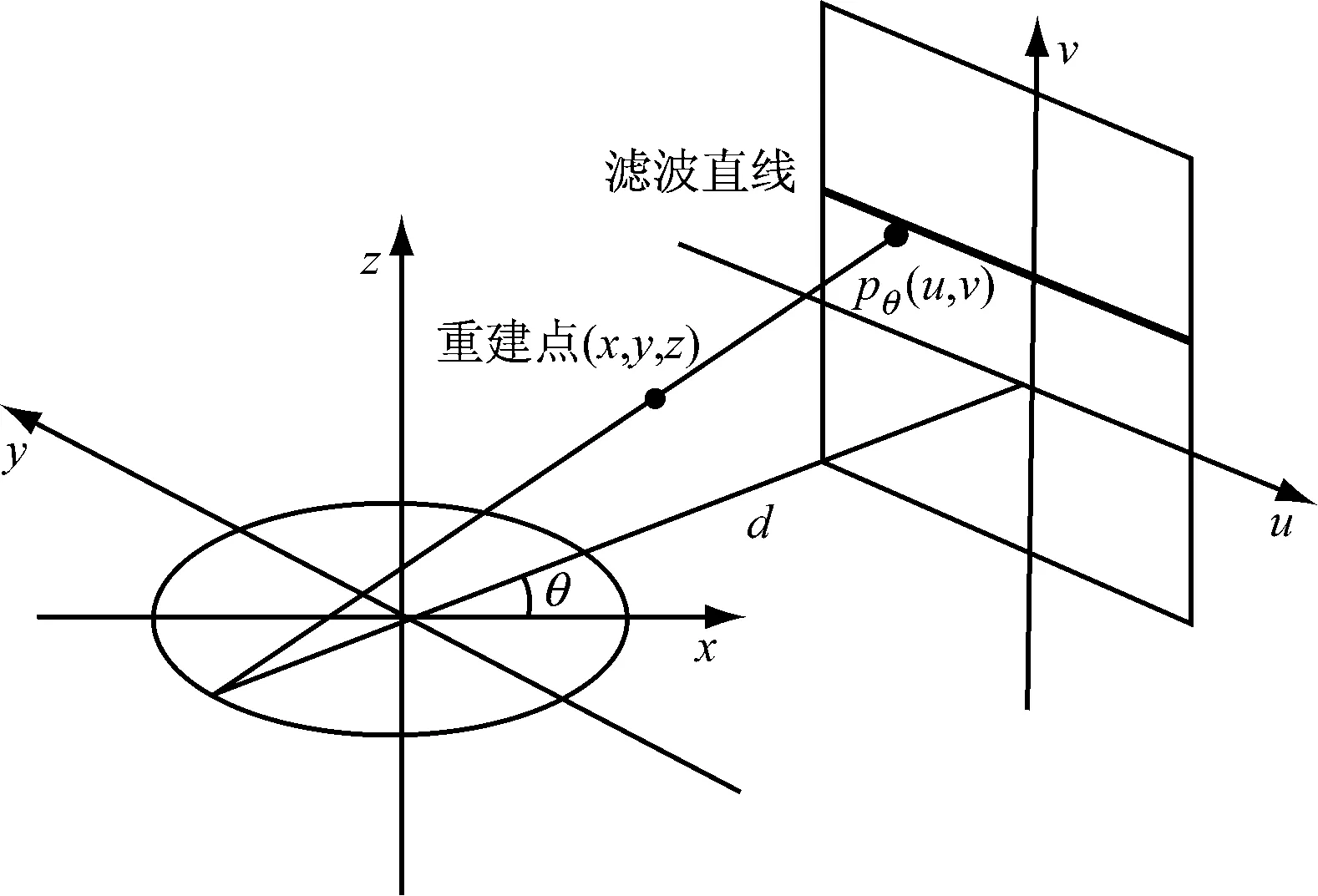
图3 FDK算法几何坐标关系

(2)对加权后的投影数据逐行进行一维频域斜坡滤波运算，如式(3)。

(2)

其中*表示卷积运算。

(3)最后沿X射线方向对滤波后的数据进行三维反投影。对经过某一像素的全部旋转角度的射线的贡献求和便得到重建的三维图像的所有像素值，如式(4)。

(4)

其中，

它们分别表示点(x,y,z)投影到探测器上的坐标。在编程过程中应使用离散计算形式，用2π/N代替dβ，用Σ代替积分，对应的反投影操作离散形式，如式(4)。

qθ(u(x,y,θ),v(x,y,z,θ)))

其中N为采样总次数。

2.3 FDK算法分析

CT扫描时射线源和探测器同步旋转一周形成的有效重建体积称为FOV(Field Of View)。它的形状为带有上下圆锥的柱体，六边形填充区域，如图4所示。

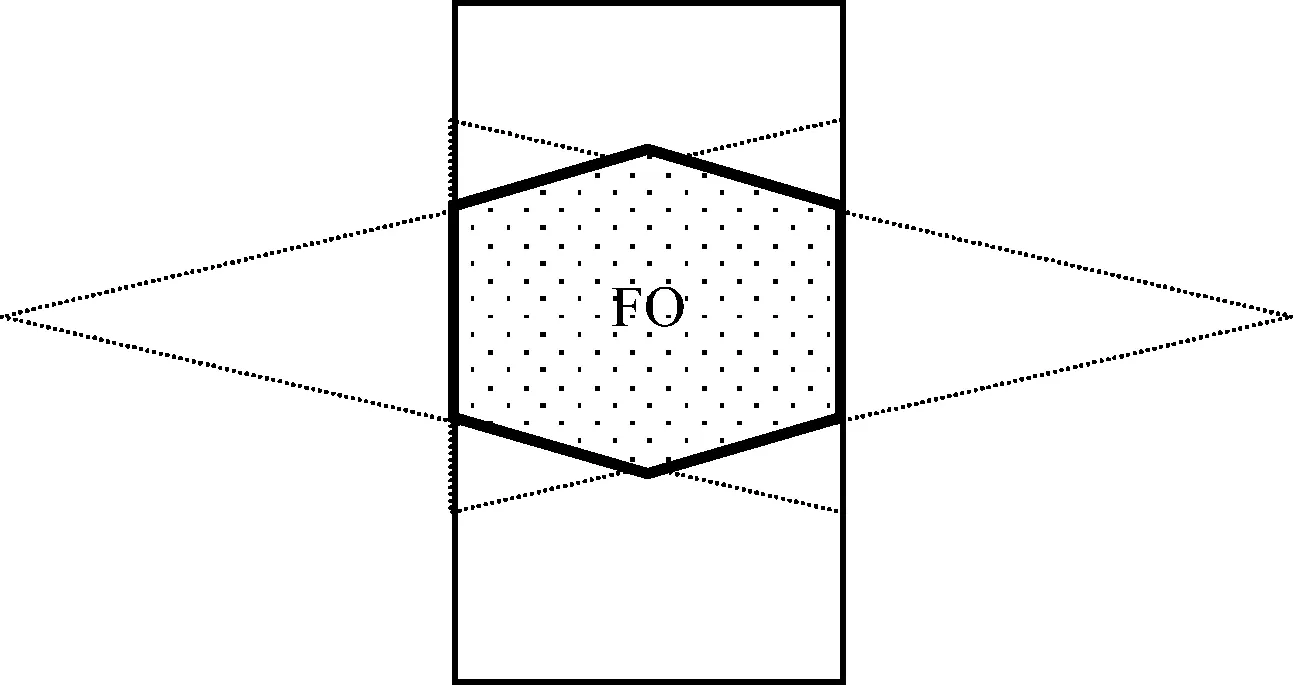
图4 FDK扫描截面和重建视野

FDK重建算法产生的三维图像中可以看到明显的伪影(Artifact Image)，特别是在偏离轨道平面的区域，其平行于x-y平面的横向切面半径变小，表现为图像上数值的偏低，和“FOV内亮外暗”现象。锥角越大，偏离越远，重建质量影响就越大，误差也更大。图5描述了伪影现象，如图5所示。

(a)真实切面(b)FDK重建切面(c)改进后重建结果切面

图5 伪影

图5(a)是真实体模在远离轨道平面区域的切面，图5(b)是FDK算法重建后对应的切面，白色三角箭头所示则是伪影。

3 改进的FDK算法

为了去除伪影，扩大有效重建面积，我们在反投影计算计算的像素值进行加权处理，使得伪影区域的像素值相对增强。处理方法为：对FDK算法重建结果乘以一个权重值α。通过判断重建点(x,y,z)在[0～2π]的每一个θ角度的投影点坐标(u,v)是否超出对应投影图像pθ(u,v)的范围，也即判断(x,y,z)在θ角度下是否被反投影，为α赋予不同的值。在计算中，对每一个重建像素点增加一个变量n, 其初始值为0。在反投影的时候，如果对应角度θ下被反投影，则对n进行自增运算。令

则最终的反投影重建，如式(6)。

qθ(u(x,y,θ),v(x,y,z,θ)))

(6)

图5(c)所示则是利用我们改进算法对远离轨道平面的切面重建后的对应结果，我们清楚地看到伪影消失了。

4 实验仿真

为验证本文对FDK改进方法是否可行，我们进行了模拟仿真实验，并将本方法和传统FDK方法重建出的图像进行对比。仿真实验使用的是基于平板探测器的圆轨道锥束CT。CT焦点到旋转中心z轴的距离为380 mm，到探测器平面的距离分为760 mm，探测器大小为512×512，探测元尺寸为1 mm×1 mm，CT扫描以1°间隔共采集360张投影数据。

体模shepp-logan在第45层的真实切面、FDK重建切面和改进后重建结果切面，如图6所示。三维图像重建大小为256×256×256，体素尺寸为1 mm×1 mm ×1 mm。图6(a)是shepp-logan体模在第128层的真实切面的切面，图6(b)是FDK算法重建后对应的切面，图 6(c)是本文方法重建出的对应层的切面图。由于该层刚好位于CT扫描轨道平面，我们可以看到本文改进算法和FDK算法的对该截面重建效果相同，并没有影响重建结果。但是相比原始FDK算法，本文提出的改进方法在没有影响原有算法精度的情况下，增大了重建体积，加大了FOV。重建结果形成一个圆柱三维体积。

(a)真实切面(b)FDK重建切面(c)改进后重建结果切面

图6 shepp-logan体模重建结果

在同样扫描几何参数下对一个头部体模进行重建结果在150层的切面，如图7所示。

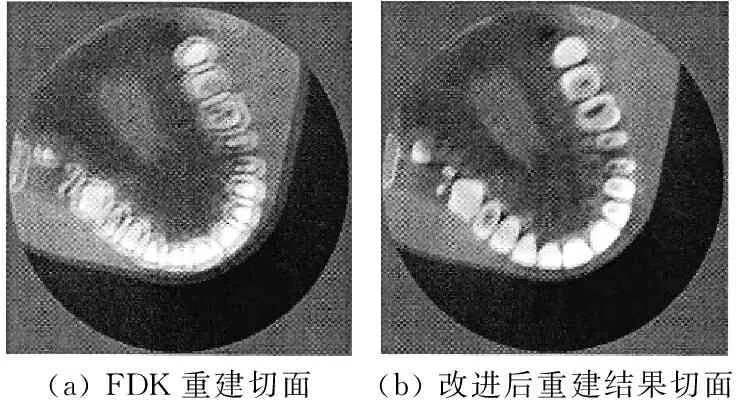
(a)FDK重建切面(b)改进后重建结果切面

图7 shepp-logan体模重建结果

三维图像重建大小为256×256×256，体素尺寸为1 mm×1 mm ×1 mm。图7(a)是FDK算法重建后对应的切面，其几何伪影较为严重，边沿模糊，分辨率低；图7(b)是用本文方法重建出的对应层的切面图，消除了伪影的干扰，分辨率高，扩大了重建体积的有效FOV。

5 总结

本文论述了CT图像重建的基本原理，并对CBCT三维重建FDK算法进行改进，扩大了重建有效体积FOV，去除伪影干扰。实验结果表明了该方法是有效可行的。修正重建结果加权因子α并把该方法运用于其它锥束CT重建算法是我们进一步的研究方向。

[1] 庄天戈. CT 原理与算法[M]. 上海：上海交通大学出版社，1992.

[2] Hsieh J, Yu Z, et al. Recent advances in CT image reconstrction[J]. Current Radioloy Reports, 2013, 1(1): 39-51.

[3] Han Yu, Li Lei, Yan Bin, et al. A half-covered helical cone beam reconstruction algorithm based on the Radon transformation[J]. Acta Physica Sinica, 2015, 64(5): 58704

[4] Du Yang, Liu Xin, Lei Yaohu, et al. Total cariation constraned iteratice filtered backprojection CT reconstruction method[J] Acta Optica Sinaica, 2016, 36(3): 0334001

[5] 韩玉,闫镔,宇超群,等. 锥束CT FDK重建算法的GPU并行实现[J]. 计算机应用,2012(5):1407-1410.

[6] 张顺利,张定华,程云勇,等. 锥束CT感兴趣区域图像重建研究[J]. 计算机应用研究,2012(9):3521-3524.

[7] 曾更生. 医学图像重建入门[M]. 北京：高等教育出版社, 2010.

[8] Yan Bin, Deng Lin, Han Yu, et al. Fast local reconstruction by selective backprojection for low dose in dental computed tomography[J]. Chinese Physics C . 2014, 38(10)：117-125.

[9] Jiang Hsieh,Brian Nett,Zhou Yu, et al. Recent Advances in CT Image Reconstruction[J]. Current Radiology Reports . 2013 ，1(1)：39-51.

[10] Feldkamp LA, et al. Practical cone-beam algorithm[J]. J Opt. Soc. Am. A., 1984, 1(6): 612-619.

[11] 曾凯,陈志强,张丽,等. 基于FDK算法的锥束CT重建近似算法性能比较[J]. 核电子学与探测技术,2004(5):511-513.