可控变质率下基于商业信用的易逝品库存优化模型
魏广明,秦娟娟,王 坤,张 茜
(1. 天津财经大学经济学院,天津 300222; 2. 天津财经大学商学院,天津 300222)
1 引言
商业信用是卖方向买方提供的一种信用,允许买方从卖方购得商品而不需要立刻支付货款,是企业间普遍采用的融资方式[ 1-2]。据金融时报报导,2007年全球商品贸易的资金90%是通过商业信用来提供的,约25万亿美元;2009年3月,Wal-Mart的资产负债表中,有28.8万亿美元的应付账款,占其持有库存的75%。许多采用商业信用支付的企业会销售易逝产品,如Wal-Mart销售蔬菜水果等易变质产品。同时,这些企业会通过一定的技术投入来降低产品的变质率,如Wal-Mart会通过提供保鲜等冷藏设备来降低蔬菜等产品的变质率。因此,论文从现实情景出发,整合易逝品供应链中,商业信用和保鲜技术投入的研究,探讨易逝品供应链中,商业信用和保鲜技术投入下,采购商的最优库存和技术投入问题,丰富有关的理论研究。
Goyal[3]首先提出了基于商业信用的EOQ模型。此后,有许多学者许多方面对上述模型进行了扩展,如缺货[ 4-5]、两级商业信用[6]、不同的市场需求函数[7]等。但上述研究常假设产品不会发生变质,但现实中许多产品价值会随着时间的推移发生变质而产生损耗,如电脑芯片,新鲜果蔬等。因此,许多学者在商业信用框架下探讨易逝品的库存策略。Aggarwal和Jaggi[8]和Chu等[9]考虑了损耗性商品在固定需求和商业信用期限下的批量问题。Jamal等[10]和Dye[11]研究了信用支付情况下,变质产品在允许缺货条件下的订货策略。Chen和Kang[12]扩展了Jamal等[10]的模型,考虑持有费用比率、收入利息、支出利息均为模糊的情形。Ouyang等[13]研究非瞬时变质产品的情形。
近年来,Balkhide[14]考虑资金的时间价值,假设存在时变变质率和时变需求率,构建了库存优化模型,结合搜索算法给出了求解步骤。Liao和Huang[15]考虑了延期支付及常数变质率下两仓储的库存决策问题。Liang Yanlai和Zhou Fangming[16]同样研究了延期付款条件下的常数变质率的库存决策问题,但其模型中租赁仓库的保管成本要高于自有仓库。Mahata[17]在指数变质率及两级商业信用下,探讨了在供应链管理中采用经济生产批量模型的采购商最优补货策略,其中假设采购商提供给顾客部分商业信用。Chang等[18]在指数变质率及两级商业信用下,构建了经济生产批量模型。Sarkar等[19], Mahata[20],Teng等[21]等虑了商业信用下,易逝品存在固定生命期限的采购商最优策略。
但是上述研究都没有考虑产品变质率的可控性,变质率常被假定为外生变量,然而现实中,通过技术的投入可影响产品的变质率的大小。但是,保鲜技术一方面可以降低易逝品的变质率,另一方面因保鲜技术投资会增加总成本的支出,因此,对商业信用下易逝品库存管理产生了难以忽略的影响(尤其是对一些高变质率的产品,如鲜花、水果)。在不考虑商业信用支付方式下,有些学者对易逝品的技术投入做了探讨。如Yang 和 Wee[22]发现了高变质率会导致高成本和低需求率。Ouyang等[23]研究了在允许延期付款的条件下,非瞬时易逝品的最优补货策略,最后提出了如果采购商通过提高易逝品储存能力可以有效地降低易逝品变质率,那么相关库存总成本也会相应降低。许多企业都投资保鲜设备来降低变质率,并且延长产品的保质期。Hsu等[24]在考虑缺货的情况下探讨了允许采购商进行保鲜技术投资的易逝品的最优库存策略。Dye和Hsieh[25]在此基础上,假设了易逝品的变质率随时间变化,最终证明了存在唯一的最优补货策略,并且发现了在给定的补货周期下每单位时间的总利润是保鲜技术成本的凹函数。上述文献中,都假设需求为常数。Hsieh和Dye[26]同样建立了一个考虑保鲜技术投资的易逝品库存模型,但假设需求随时间变化。而He Yong和Huang Hongfu[27]假设了需求与价格呈线性关系,讨论了考虑保鲜技术投资的季节性易逝品的最优库存策略和价格政策。
因此,本文将可以降低易逝品变质率的保鲜技术引入商业信用下易逝品库存模型中,从采购商的角度出发,考虑到保鲜技术对总利润的影响,分析了在商业信用支付策略下易逝品的最优库存策略及技术投入策略。首先,分两种情形讨论了考虑保鲜技术投入后,采购商的利息收入和利息支出,建立了相应的决策模型。其次,通过模型的分析求解,得出了采购商的最优订货周期和最优保鲜技术投资水平的判定方法;最后,通过数值分析对有关结论进行了验证,并进一步分析了各参数对采购商最优决策的影响。
2 符号与假设
2.1 主要符号
论文用到的主要符号如下:
A: 采购商的固定订货成本;
s:采购商的单位销售价格;
c:采购商的单位采购价格,s≥c;
h:采购商的单位库存持有成本(不计利息支出);
D:产品的市场需求量;
Ie:单位利息收入率;
Ik:单位利息支出率;
T:采购商的订货周期,为决策变量;
Q:采购商的订货批量;
M:供应商提供给采购商的商业信用期;
θ:产品的自然变质率;
β:单位时间内保鲜技术的投资成本,为决策变量;
I(t):随着时间t变化的库存水平;
TP: 单位时间采购商的销售利润。
2.2 模型假设
(1)考虑由供应商和采购商组成的两级供应链,采购商只采购一种产品,不允许缺货。
(2)订货提前期为0,即瞬时补货。
(3)供应商提供给采购商的商业信用期为M。在商业信用期内,采购商不需要支付货款,且可以利用销售收入获得一定的利息。
(4)为了减少产品变质给企业所带来的损失,企业可以通过保鲜技术的投入来降低其变质率。例如,企业可以通过运行冷藏设备等来降低蔬菜水果的变质率,那么在单位时间内,冷藏设备的运营成本即为单位时间内保鲜技术的投资成本。引入保鲜技术后产品的变质率为θ-η(β),且η(β)=θ(1-e-∂β),其中∂η(β)/∂β<0,∂2η(β)/∂β2>0。θ为自然变质率,满足0≤θ<1;是保鲜技术投资对变质率的敏感系数,∂≥0;β为单位时间内保鲜技术的投资成本,β≥0,为决策变量[26-27]。
3 模型构建
在订货周期T内,库存水平的下降由市场需求和产品的变质引起,因此,采购商的库存水平变化可以用以下微分方程来表示:
dI(t)/dt=-D-[θ-η(β)]I(t)
(1)
其满足的边界条件为.
由式(1),计算可得采购商的库存水平为:
(2)
采购商单位周期的订货量为:
(3)
采购商的单位周期利润由以下几部分构成:销售收入,固定订货成本,采购成本,库存保管成本,保鲜技术投资成本,利息支出和利息收入。
(1) 单位时间保鲜技术投资成本:β;
(2) 销售收入:sD;
(5) 单位时间的库存保管成本(不包括库存资金成本):
(6) 利息收入和利息支出的分析见3.1 和3.2。
根据商业信用期M和订货周期T之间的关系,采购商的利息收入和利息支出分为以下2种情况:M>T和M≤T.
3.1 情形一.M>T
当供应商提供给采购商的商业信用期M大于销售商订货周期T时,采购商在信用期M内取得了所有的销售货款,可以及时地向供应商支付采购费用,因此,无需支付库存资金成本,即利息支出为0。
采购商在T时刻取得了全部销售收入,因此在[0,T]内可以获得已取得销售收入的利息收益,而在[T,M]内可以获得全部销售收入的利息收益。因此,利息收入为:
(4)
3.2 情形二.M≤T
由于供应商允许延迟付款,因此在[0,M]内采购商可以取得已取得销售收入的利息收益。因此,利息收入为:
(5)
由于M≤T,在信用期M内,采购商没有取得所有销售货款,因此需要支付在[M,T]内的库存资金成本。因此,利息支出为:
(6)
通过以上分析,可得采购商的利润表达式:
采购商单位周期的利润=销售收入-固定订货成本-采购成本-库存保管成本-保鲜技术投资成本-利息支出+利息收入
其中,
(7)
(8)
4 最优解分析
4.1 最优订货周期T
情形一 .T≤M
为了求解该区间内采购商的最优订货周期,可以对T求一阶、二阶偏导数,计算一阶导数可得:
其中:
(9)
易得:
(10)
TP1(T|β)对T的二阶导数为:


满足以上条件的T1就是可以使式(7)取得最大值的T。如果0 通过分析,我们可以得到命题1。 命题1.对于任意β≥0 (1)T1不但存在而且是唯一解。 (2)如果0 (3)如果T1≥M,TP1(T|β)在T≤M的条件下可以在M处取得最大值。 情形二.M≤T 为了得到最优的订货周期,我们可以求TP2(T|β)对T的一阶偏导: (11) 其中: (12) f2(T|β)对T求偏导可得: (13) TP2(T|β)对T求二阶偏导为: 通过以上分析,可得命题2。 (1)T2不但存在而且是唯一解。 (2)如果0 (3) 如果T2≥M,函数TP2(T|β)在T≥M的条件下可以在T2处取得最大值。 通过以上命题1、2的分析,易得定理1(关于最优订货周期的决策)。令: Δ=f1(T|β)|T=M=f2(T|β)|T=M 定理1. 对于任意β≥0,当A-sDIeM2/2>0时 (1)如果Δ>0,采购商的最优订货周期是T2. (2)如果Δ=0,采购商的最优订货周期是M. (3)如果Δ<0,采购商的最优订货周期是T1. 情形一.T≤M 由式(8),可知利润函数TP1(|β|T)可写为: 由泰勒展开式可证: (15) (16) (17) δ′(x)=-Tη′(x)<0;δ″(x)=-Tη″(x)>0 (18) λ′(x)=-cDTη′(x)<0;λ″(x)=-cDTη″(x)>0 (19) 由此,可计算: [λ(x)φ(δ(β))]′=λ′(x)φ(δ(β))+λ(x)φ′(δ(β))δ′(β) [λ(x)φ(δ(β))]″=λ″(x)φ(δ(β))+2λ′(x)φ′(δ(β))δ′(β)+λ(x)φ″(δ(β))δ(β)2+λ(x)φ′(δ(β))δ′(β)>0 情形二.M≤T 由式(9),可知利润函数TP2(|β|T)可写为 (20) 与情形一的分析类似,可得定理3. 为了说明模型及定理的可行性,下面我们来举例说明。 例:设定某采购商制定某产品的进货策略,数据如下:A=20元/次,D=100件/年,s=25元/件,c=15元/件,h=5元/件/年,M=0.1天/年,θ=0.2/年,∂=0.5,Ie=0,09,Ik=0.14. 易证:A-sDIeM2/2=17.75>0,满足命题2的条件。因此,计算可得采购商的最优策略为: 在算例的基础上,调整模型各参数值,可以得到采购商的最优决策结果见表1。通过敏感性分析,可以更清楚的看出参数的变化对零售商的最优订货策略和最优技术投入策略的影响。 表1 参数对最优决策的敏感性分析 从表1的各参数对最优解的灵敏度分析,可以得出以下结论: (1) 当保鲜技术投资对变质率的敏感系数增加时,最优保鲜技术投资量会降低,最优订货周期和总利润会增加。也就说,对企业而言,如果保鲜技术投资对产品变质率有较强影响时,采购商不需要太多的保鲜技术投资投入,同时由于技术投入引起产品变质率的降低,因此采购商不需要太频繁的订货,可以延长最优订货周期。反之,当保鲜技术投资对变质率的敏感系数减小时,为了降低变质率,采购商会增加对保鲜技术的投资。 (2) 当产品的自然变质率增加时,最优保鲜技术投资量会增加,最优订货周期不变,总利润会减少。当产品的变质率减小时,采购商会降低保鲜技术投资量,则其利润会增加。 (3) 随着采购商订货费用的增加,采购商的最优保鲜技术投资量和最优订货周期增加,总利润减少。结论表明,当采购商的单次订货费用支出较高时,采购商可能会增加每次的订货量从而增加了订货周期的长度,由于订货数量的增加需要加大保鲜技术投资以降低变质率。 (4) 随着市场需求率的增加,采购商的最优保鲜技术投资量和总利润会增加,最优订货周期减小。当市场需求较好时,采购商为了满足市场需求将提高订货频率,相应的订货周期长度会减小,由于市场需求增加,产品的库存时间相应缩短,保鲜技术的投资也会降低。 (5) 当供应商给予采购商的商业信用期增加时,最优保鲜技术投资量和最优订货周期都会减小,而利润会增加。当供应商给予采购商的商业信用期较长时,采购商可以相应获得更多的利息收益,因此可以抵消由于订货周期减少而带来的订货成本的增加,并且因为订货批量的下降,可以进一步减少变质损失,减少保鲜技术投资量。 (6) 当产品的售价增加时,采购商的最优保鲜技术投资量和最优订货周期会减少,总利润会增加。当易逝品价格增加时,消费者需求会降低,采购商为了降低成本,会缩短订货周期和保鲜技术的投资量。 (7) 随着采购商单位库存持有成本的增加,最优保鲜技术投资量、最优订货周期和总利润都会减小。对于采购商来说,当单位库存持有成本增大时,采购商会减少订货周期来降低库存持有成本,相应也会减小保鲜技术投资。 (8) 随着采购商采购产品的成本增加,最优保鲜技术投资量会增加,最优订货周期不变,总利润会减少。当采购商采购产品的成本增加,采购商为了节约成本会加大保鲜技术的投资以降低产品变质率。 文章在商业信用支付模式下,探讨了考虑产品保鲜技术投入下,采购商的最优订货策略及技术投入策略。首先,分两种情形构建了采购商的库存模型;其次,根据采购商的库存模型,求解其最优订货周期、最优订货量及其最优技术投入策略;最后,通过数值分析对文章中的有关结论进行了验证,并对有关参数进行了灵敏度分析。 研究发现:当保鲜技术投资对产品变质率有较强影响时,采购商不需要太多的保鲜技术投资,同时由于技术投入引起产品变质率的降低,因此采购商不需要太频繁的订货,可以延长最优订货周期;产品的自然变质率增加时,采购商为了降低变质率会增加保鲜技术投资量,总利润会减少。当产品的自然变质率减小时,采购商会降低保鲜技术投资量,利润会增加;当采购商的单次订货费用支出较高时,采购商可能会增加每次的订货量从而增加了订货周期长度,由于订货数量的增加需要加大保鲜技术投资以降低变质率;当市场需求较高时,采购商为了满足市场需求将提高订货频率,相应的订货周期长度会减小,由于市场需求增加,产品的库存时间相应缩短,保鲜技术的投资也会降低;当供应商给予采购商的商业信用期增加时,最优保鲜技术投资量和最优订货周期都会减小,而利润会增加。 [1] Fisman R, Love I. Trade credit, financial intermediary development, and industry growth[J]. Journal of Finance, 2003, 58(1): 353-374. [2] Yang S, Brige J. How inventory is (should be) financed: Trade credit in supply chains with demand uncertainty and costs of financial distress[R].Social Science Research Netwrok,2011, http://dx.doi.org/102139/ssrn.1734682. [3] Goyal SK. Economic order quantity under conditions of permissible delay in payments [J].The Journal of the Operational Research Society, 1985, 36(4):335-338. [4] Khanra S, Mandal B, Sarkar B. An inventory model with dependent demand and shortages under trade credit policy [J].Economic Modelling, 2013, 35(9):349-355. [5] Zhong Yuanguang, Zhou Yongwu. Improving the supply chain’s performance through trade credit under inventory-dependent demand and limited storage capacity [J].International Journal of Production Economics, 2013, 143(2):364-370. [6] 赵忠, 王淑云, 李波. 时变需求下基于两级信用支付的易腐品订货模型[J]. 系统管理学报, 2016, 25(1): 83-89. [7] 秦娟娟. 时变供需下基于商业信用的零售商最优订货策略[J]. 中国管理科学, 2016, 24(3): 89-98. [8] Aggarwal S P, Jaggi C K. Ordering policies of deteriorating items under permissible delay in payments [J]. Journal of the Operational Research Society, 1995, 46(5):658-662. [9] Chu P, Chung K H, Lan S P. Economic order quantity of deteriorating items under conditions of permissible delay in payments [J]. Computer and Operations Research, 1998, 25(10): 817-824. [10] Jamal A M, Sarker B R, Wang S. An ordering policy for deteriorating items with allowable shortage and permissible delay in payment [J]. The Journal of the Operational Research Society, 1997, 48(8): 826-833. [11] Chang H J, Dye C Y. An inventory model for deteriorating items with partial backlogging and permissible delay in payments [J]. International Journal of Systems Science,2001, 32 (3): 345-352. [12] Chen L H, Kang F S. Integrated vendor-buyer cooperative inventory models with variant permissible delay in payments [J]. European Journal of Operational Research, 2007, 183(2): 658-673. [13] Ouyang L Y, Wu K S, Yang C T. A study on an inventory model for non-instantaneous deteriorating items with permissible delay in payments [J]. Computers & Industrial Engineering, 2006, 51(4): 637-651. [14] Balkhi Z T. Optimal economic order policy with deteriorating items under different supplier trade credits for finite horizon case [J]. International Journal of Production Economics, 2011, 133(1):216-223. [15] Liao J J, Huang K N. Deterministic inventory model for deteriorating items with trade credit financing and capacity constraints [J]. Computers & Industrial Engineering, 2010, 59(4):611-618. [16] Liang Yanlai, Zhou Fangming. A two warehouse inventory model for deteriorating items under conditionally permissible delay in payment [J]. Applied Mathematical Modelling, 2011, 35(5):2221-2231. [17] Mahata G. An EPQ-based inventory model for exponentially deteriorating items under retailer partial trade credit policy in supply chain [J]. Expert Systems with Applications, 2012, 39(3):3537-3550. [18] Chang C T, Teng J T, Chern M S. Optimal manufacturer’s replenishment policies for deteriorating items in a supply chain with up-stream and down-stream trade credits [J]. International Journal of Production Economics, 2010, 127(1):197-202. [19] Sarkar B, Saren S, Cárdenas-Barrón L E. An inventory model with trade-credit policy and variable deterioration for fixed lifetime products [J]. Annals of Operations Research, 2015, 229(1): 677-702. [20] Mahata G C. Optimal ordering policy with trade credit and variable deterioration for fixed lifetime products [J]. International Journal of Operational Research, 2016, 25(3): 307-326. [21] Teng J T, Cárdenas-Barrón L E, Chang H J, et al. Inventory lot-size policies for deteriorating items with expiration dates and advance payments [J]. Applied Mathematical Modelling, 2016, 40(19): 8605-8616. [22] Yang P C, Wee H M. A collaborative inventory system with permissible delay in payment for deteriorating items [J]. Mathematical and Computer Modeling, 2006,43(3-4):209-221. [23] Ouyang L Y, Wu K S, Yang C T. A study on an inventory model for non- instantaneous deteriorating items with permissible delay in payments [J]. Computers and Industrial Engineering, 2006, 51(4): 637-651. [24] Hsu P H, Wee H M, Teng H M. Preservation technology investment for deteriorating inventory [J]. International Journal of Production Economics, 2010, 124(2): 388-394. [25] Dye C Y, Hsieh T P. An optimal replenishment policy for deteriorating items with effective investment in Preservation Technology [J].European Journal of Operational Research, 2012, 218(1): 106-112. [26] Hsieh T P, Dye C Y. A production inventory model incorporating the effect of preservation technology investment when demand is fluctuating with time [J]. Journal of Computational and Applied Mathematics, 2013, 239: 25-36. [27] He Yong, Huang Hongfu. Optimizing inventory and pricing policy for seasonal deteriorating products with preservation technology investment [J].Journal of Industrial Engineering,2013, 2013: 1-7.


4.2 最优保鲜技术投资ζ
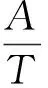
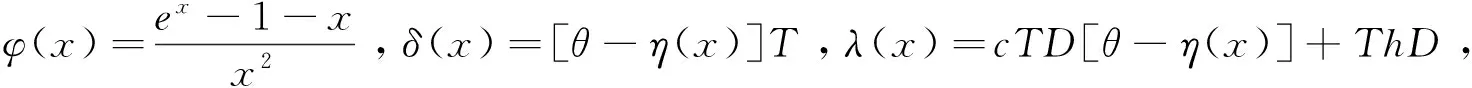
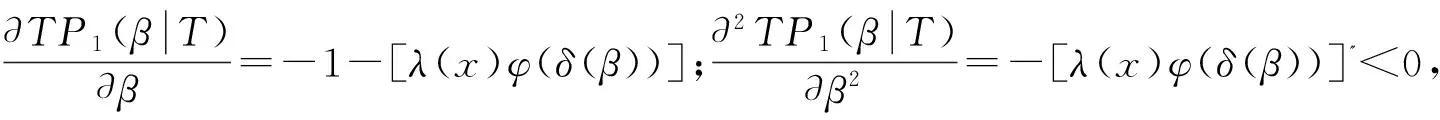
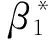
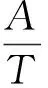
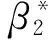
5 数值分析
5.1 算例
5.2 敏感性分析

6 结语

