供应风险下营业中断保险的供应链模型分析

于 辉, 吴腾飞

(重庆大学经济与工商管理学院, 重庆 400030)

1 引言

各种突发事件和灾害(如火灾、地震、洪水等)正越来越频繁地冲击着供应链，而供应链全球化进一步加剧了供应链风险，尤其是供应风险。在对我国中小板上市企业(共743家)的招股说明书风险说明的统计中，有65%的企业声明其采购面临来自供应侧的不确定风险。营业中断保险作为风险管理的重要手段，已在实践中得到有效应用。如2000年飞利浦的一家芯片厂发生火灾，其下游企业Ericsson获营业中断保险赔偿2亿美元[1]；汶川地震后的拉法基公司也因营业中断保险获赔7.2亿[2]。因而，针对日益加剧的供应链供应风险，把营业中断保险引入供应链进行研究具有重要的意义。

目前，学者对供应链供应风险管理的研究主要集中在运营策略的研究。制定恰当的库存策略[3]是企业在多周期模型下应对供应风险的手段。企业间应急援助[4]、采用备用供应商[5]、应急期权[6]也被证实是应对供应风险的有效手段。现有文献对营业中断保险的研究主要可以分为三类。一是保险产品介绍类，主要是对承保、赔偿等实务环节进行说明以及对中外营业中断保险的比较[7-8]。二是应用研究类，部分学者[9-11]结合具体的世界著名案例探讨了营业中断保险对企业利润损失的补偿作用。还有学者研究了运营策略和营业中断保险在风险管理中的关系，他们发现营业中断保险可以部分替代库存，补偿企业利润损失，帮助企业应对供应风险[12-13]。此外，还有少部分学者考察了营业中断保险对供应链的影响，他们认为营业中断保险帮助供应链管理了供应风险[14-15]。三是技术细节研究类，Adams[16]提出了运用计量模型来预测营业中断保险中的预期损失。

舒磊等[17]针对确定需求建立了供应不可靠(随机)下的风险厌恶采购单阶段模型，证明了库存策略应对企业供应风险的有效性。Dong Lingxin和Tomlin等[12]在需求确定且供应风险导致企业产量为0的情况下，研究了运营策略(库存和紧急采购)和营业中断保险的相互影响。米俊毅等[18]通过建立结构方程模型研究了保险对物流业的影响并进行了实证分析，结果表明保险对物流业具有显著的促进效用。秦绪伟等[19]首次尝试对维修服务运作与营业中断保险进行跨界研究，他们用泊松分布刻画企业设备故障过程，发现保险费率(外生)影响企业投保的意愿。这些研究为我们在供需两侧都随机的情况下探讨营业中断保险对供应链风险的管理打下了基础。一些学者[14-15]把营业中断保险和供应链结合起来研究时大多假设保费费率外生，作为对他们研究的延伸，我们进一步探讨费率内生的问题并研究了保险公司的决策。本文是从供应链风险管理和运营与保险相结合的视角出发，用随机供应刻画供应风险，在需求也不确定的情况下，研究了供应链和营业中断保险的相互影响；并且还让保费费率内生，考察了保险公司的决策，最终得到了三方共赢的结果。

本文先分别刻画并求解了供应风险下供应商不投保和投保的供应链模型，然后对比分析两种模型的求解结果，接着研究了保险公司的费率决策，最后用数值仿真验证前面的结果并得出结论。本文揭示出通过对保费投资收益和供应风险的权衡，保险公司制定合理的费率后，投保可以实现三方共赢。此外，本文还发现营业中断保险的投保促进了供应链的合作，反过来供应链合作也使营业中断保险的价值得到扩展，运营结合保险是互利的。

2 基准模型

考虑由单个供应商和零售商组成的二级供应链系统，零售商面临随机市场需求D(概率密度函数f(.) ，累积分布函数F(.))。由于面临突发事件、质量问题和运输损毁等带来的供应风险，供应商的交货量是随机的[20]，其单位生产成本为c。双方订立批发价契约，供应商先制定批发价格，零售商同时考虑供需两侧的不确定性进行订货决策。最后，供应商进行生产后向零售商供货，零售商按市场决定的价格p销售产品。

图1 不投保模型系统流程图

本小节的基本假设如下：

1)零售商、供应商是风险中性的，追求各自期望利润最大化；

2)供应风险针对供应商的产成品(如成品库火灾，运输损毁等)，从而造成供应商交货量随机，但是生产成本已经发生；

3)ξ是取值介于0和1之间的随机交货因子(交货量与订货量之比)，概率密度函数是g(.) ，累积分布函数是G(.)，均值u，方差是σ2；

4)供应链双方的信息是对称的。

零售商利润函数：

(1)

供应商利润函数：

E[πS(w)]=E(wξq-cq)=wuq-cq

(2)

本文假设市场需求服从均匀分布，一是为了模型求解的方便，二是本文主要关注的是营业中断保险用于解决供应风险，而需求服从的具体分布不会对研究结论产生实质性的影响。现实中，在需求信息有限时，均匀分布常被作为近似分布来研究问题，其他需求分布的研究可以参考均匀分布的分析。

证明：分别对(1)式关于q求一阶和二阶偏导：

(3)

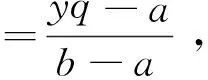
分别对(2)关于w求一阶和二阶偏导：

3 供应商投保的模型

3.1 营业中断保险

营业中断保险是指对企业(被保险人)因遭受自然灾害或意外事故等，在一段时间内停产、停业或营业受影响导致的经济损失及营业中断期间发生的必要费用支出提供保障的保险[21]。

本文为了清楚刻画营业中断保险对供应链的影响而采用了英国的保险模式——营业中断保险可以单独投保[22]。而在美国和中国，营业中断保险是财产保险的附加险。在中国，只有投保了财产保险才能投保营业中断保险；且只有前者得到了赔偿，营业中断保险才能得到赔偿。

3.2 包含营业中断保险的供应链模型

考虑由单个供应商和零售商组成的二级供应链系统，面临供应风险的供应商引入保险公司作为风险分担者。供应商和保险公司订立保险契约，保险公司制定保费费率r，供应商确定保险额度L(保险公司的最大赔偿)，交保费rL。供应商还和零售商订立批发价契约，供应商先制定批发价格(与保额同时决策)，零售商同时考虑供需两侧的不确定性进行订货决策。接下来，供应商进行生产后向零售商供货，如果有供应风险造成的利润损失，供应商向保险公司索赔并得到赔偿。最后，零售商销售产品。

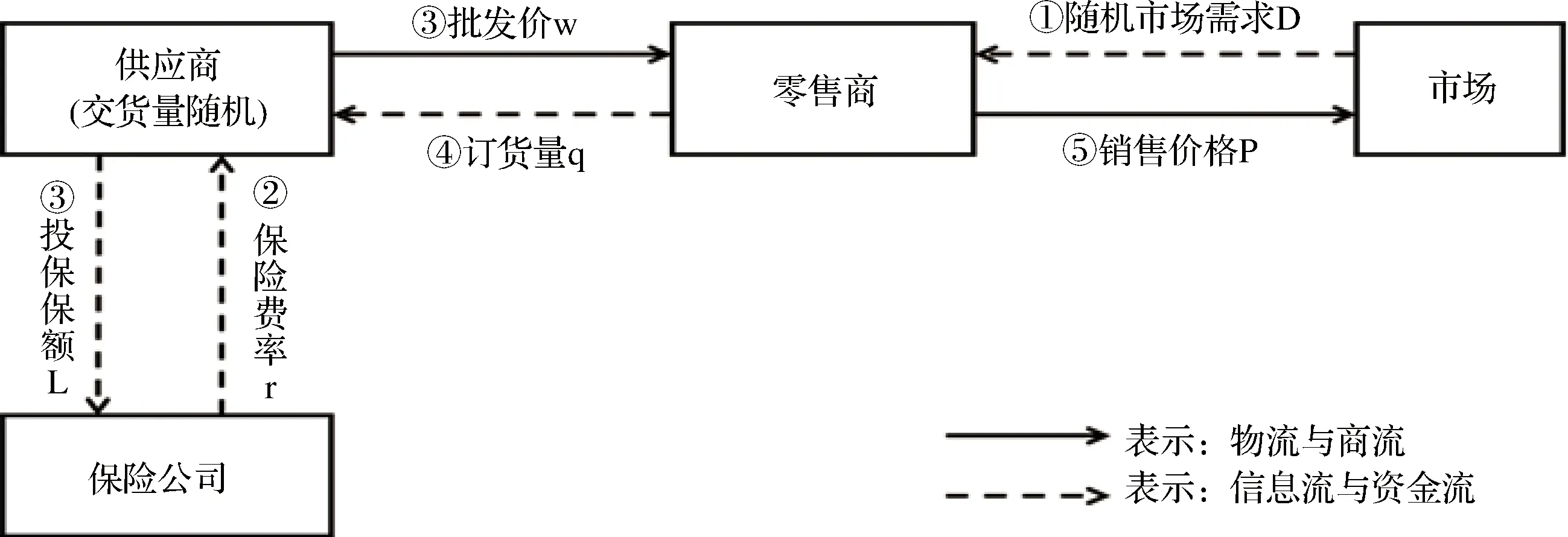
图2 投保模型系统流程图

本小节的基本假设如下：

1)零售商、供应商和保险公司是风险中性的，追求各自期望利润最大化；

2)供应风险针对供应商的产成品，从而造成供应商交货量随机，但是生产成本已经发生；

3)ξ是取值介于0和1之间的随机交货因子，概率密度函数是g(.) ，累积分布函数是G(.)，均值u，方差是σ2；

4)系统所有参与者的信息是对称的；

5)产品数量损失只由保险合同承保的灾害、事件等引起。

零售商制定订货量q后，供应商正常情况下的利润是(w-c)q，存在供应风险后其实际利润是wξq-cq，因此供应商的利润损失K=(1-ξ)wq。因为保额L是保险公司的赔偿上限，所以保险赔偿是min{K,L}。

3.3 模型求解

零售商利润函数：πR(q)=pmin{ξq,x}-wξq=p[eξq-(ξq-x)+]，e=(1-w/p)，

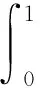
(4)

供应商利润函数：πS(w,L)=wξq-cq+min{K,L}-rL，0≤L≤wq，0≤r≤1，

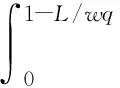
(5)

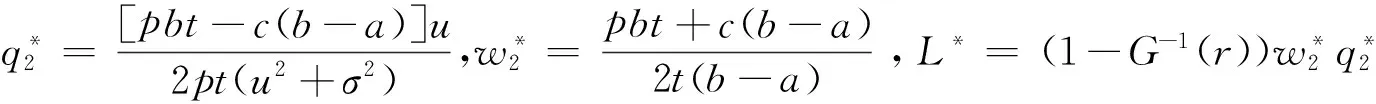
证明：给定批发价和需求分布，供应商投保于否，零售商的期望利润都不变。由定理1的证明知：

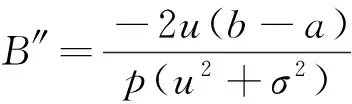
依次对(5)关于L求一阶和二阶偏导：

E[πS(w,y)]的海赛矩阵是：

因为Fww<0，所以E[πS(w,L)]是w、L的凹函数，存在最大值且在驻点处取得。

推论1 无论随机交货因子服从什么分布，供应商投保后，供应链批发价降低，订货量增加，供应链双方的利润增加。

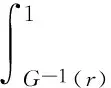
推论1的结论可以解释为：供应商投保后，如果突发事件导致利润损失，供应商会得到保险赔偿，因此供应商会降低批发价，这刺激了零售商增加订货量。

命题1 保费费率越大，供应商投保的情况相对于不投保情形，供应链双方各自的利润增加越少。

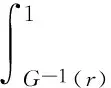
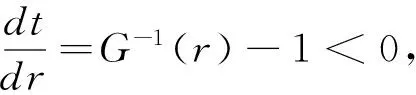
推论2 保费费率越高，供应商投保的保额越低。

4 保险公司的决策

保险公司会用供应商交的保费去投资，假设投资收益是R，因此保险公司的利润是：

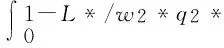
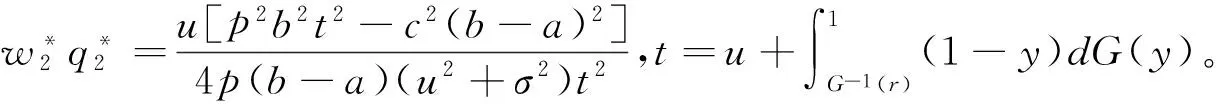
由E[πI(r)]的表达式可以得到如下定理：

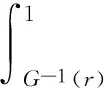
此式表明为了让供应商投保实现三方共赢，保险公司制定费率r时需要权衡保费投资收益R和供应风险(G(y))。现实中，保险定价还要考虑市场的竞争因素。目前，我国保险行业是买方市场，保险公司一般会选择满足定理3中条件的最小r值作为费率。一些保险公司为了抢占市场份额，甚至把费率定在利润的零点。

如果要求最优费率，需要让随机交货因子的分布具体化。现实中，在信息有限时，均匀分布常被作为近似分布来研究问题。于是我们选取了均匀分布进行分析并得到了命题2。由于积分限涉及分布函数的反函数，一般分布类型的求解非常复杂。但是其他分布类型可以参考均匀分布的分析，因为均匀分布的情形有一定的代表性(后面的仿真可印证)。

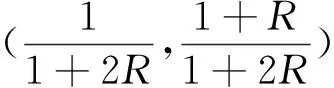
[1+R-(1+2R)r][p2b2t3-(b-a)2c2t]-(b-a)2c2(r-1)2(2Rr+r-1)=0

使得保险公司的利润最大，其中t=0.5[(1-r)2+1]。

证明：若ξ～U(0,1)，则当0≤x≤1时，g(y)=1,G(y)=y,G-1(y)=y。于是有:

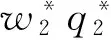
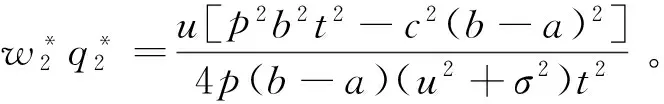
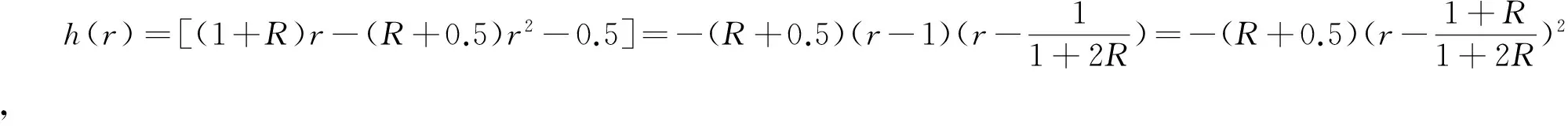
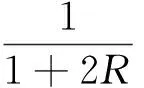
E[πI(r)]的一阶导数是：

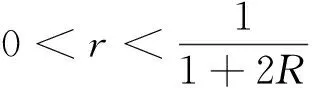
E′[πI(r)]=k1{[1+R-(1+2R)r][p2b2t3-(b-a)2c2t]-(b-a)2c2(r-1)2(2Rr+r-1)}=0

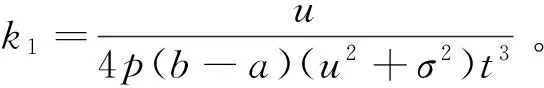
下面证明r*是唯一的最大值点：

其中：

v(r)=(2R+1)t2[p2b2t2-(b-a)2c2]+4(b-a)2c2t(1-r)[1+R-(2R+1)r]，

l(r)=(b-a)2c2[1-5(1-r)2][(1+R)r-(R+0.5)r2-0.5]=(b-a)2c2[1-5(1-r)2]h(r)。

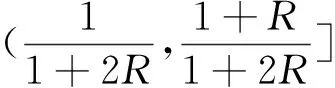
lM=

为了判定二阶导数的正负，对vm、lM作差得到：

16(vm-lM)(1+2R)7=p2b2[R2+(1+2R)2]4-4(b-a)2c2[(1+2R)8+4R2(1+2R)6-9R4(1+2R)4][R2+(1+2R)2]4-[(1+2R)8+4R2(1+2R)6-9R4(1+2R)4]>0

再结合前面连续函数的零点定理可以得出r*是唯一的最大值点。

5 数值仿真

为了更好地对供应商不投保、投保这两种情形进行比较以及更好地理解保险公司的定价决策, 下面利用数值仿真分析：1)营业中断保险对供应链的影响和价值；2)保费费率对供应商投保保额和保费支出的影响；3)交货因子服从不同分布下保险公司的利润随保费费率的变化。

β分布是取值介于0和1之间的随机变量的概率分布。若X～β(m,n)，其概率密度函数f(x)=kxm-1(1-x)n-1,0≤x≤1，m、n>0，均匀分布是两个参数都为1时的β分布。因此为了使仿真结果更具代表性，无特别说明，接下来我们都采用了β分布(m=0.3,n=2)进行仿真。相关参数由表1给出：

表1 相关参数设定表

5.1 供应商投保与不投保情形的对比

由图3和图4可以看出供应商投保后，无论费率取什么值，订货量和供应商双方的利润都是增加的。但是随着费率的增大，增加的幅度都是逐渐减小的。投保后，供应商损失会得到一定赔偿，其会降低批发价，这刺激了零售商增加订货量。在费率的一定范围内订货量甚至超过了需求上界，零售商面临的供应链风险得到降低。通过供应链的传导作用，保险的价值从投保企业扩展到下游未投保企业，一家企业投保两家企业受益，达到事半功倍的效果。

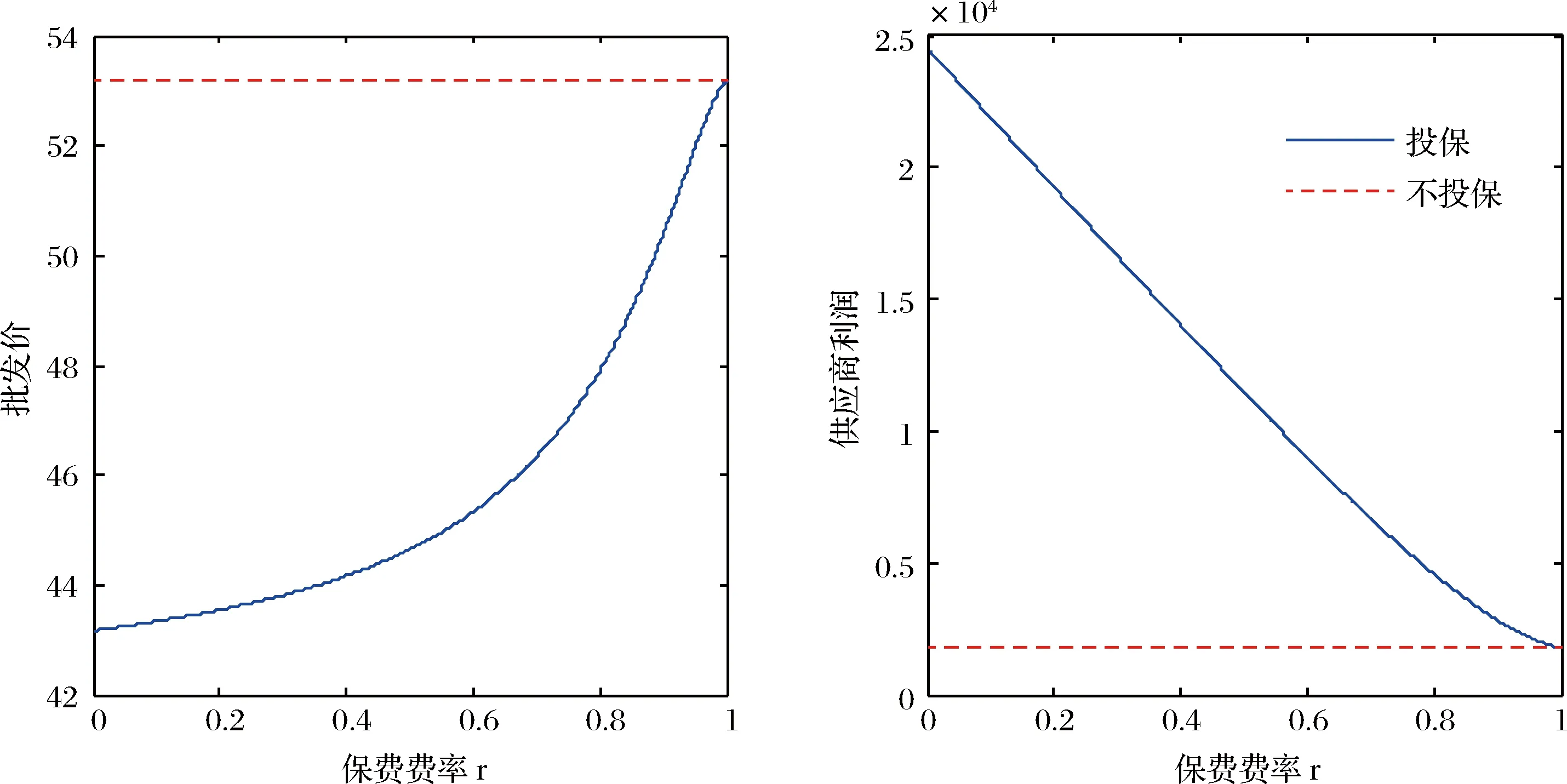
图3 两种模型供应商批发价及利润的对比

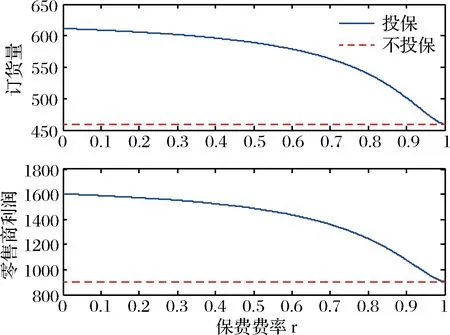
图4 两种模型零售商订货量及利润的对比

5.2 供应商投保的保额与保费

由图5可知，费率越高，供应商投保的保额(保险公司的最大赔偿)越低，保险公司可以通过调整费率来控制赔偿的上限，防止亏本甚至破产。但是随着费率的增加保险公司的保费收入先增加后减小，保险公司需要对费率作出权衡。

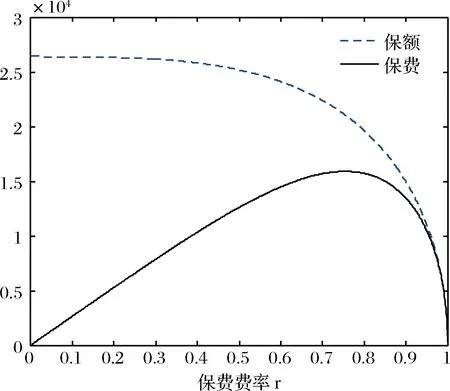
图5 保额及保费

5.3 保险公司的定价决策

为了验证命题2中均匀分布情形的代表性，我们分别对随机交货因子服从均匀分布和β分布的情况进行了仿真(取R=0.3)。

观察图6可知，保险公司的利润函数在随机交货因子服从均匀分布和β分布时具有类似的特征：都是费率的凹函数；在费率的一个区间内取正值；最优费率唯一。这说明随机交货因子服从均匀分布时与保险公司决策相关的结论(命题2)具有一定的代表性。其他分布情形的研究可以参考均匀分布情形的分析过程。

仿真求出的最优费率如表2所示，可以看出随机交货因子是均匀分布时，最优费率确实在命题2给出的对应区间内，命题2得到验证。

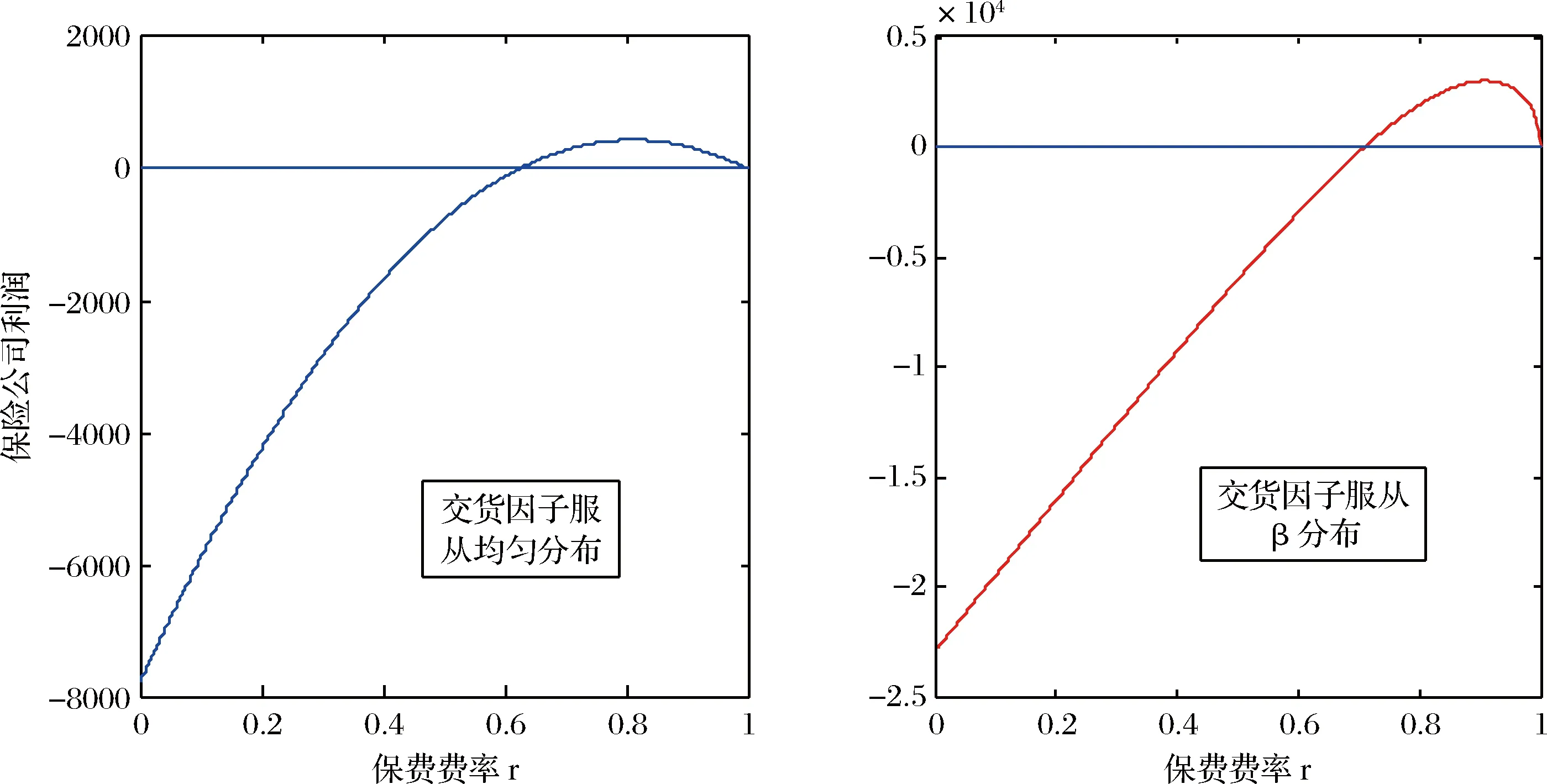
图6 保险公司利润

随机产出分布最优费率命题2中区间U(0,1)0.8116(0.6250,0.8125)

6 结语

面对不确定的灾害和事故等供应风险，供应链非常有必要结合营业中断保险来应对风险和保障利润。本文在供需不确定的情况下通过建立供应商 、零售商、保险公司三方参与博弈的供应链模型，研究了供应链和营业中断保险结合后的相互影响以及保险公司的费率决策。研究结论如下：

(1)保险公司合理定价后，投保能够实现三方共赢。通过对保费投资收益和供应风险的权衡，保险公司制定合理的费率后，投保使供应链双方和保险公司都获利，三方共赢得以实现(定理3)。保险公司可以通过调整费率来控制赔偿的上限。保险公司提高费率，供应商会相应降低投保的保额，赔偿的上限得到控制，防止亏本甚至破产。但保额低了会影响保费收入，保险公司需要对费率做出权衡(推论2，图5)。

(2)投保营业中断保险后，面临供应风险的供应链的绩效得到改善。相较于不投保的情形，供应商投保后，供应链中的批发价格降低了，订货量及供应链双方利润都增加了。供应链双方利润的增加实质是双方的利润损失都得到了一定补偿。因此，营业中断保险帮助供应链应对了风险。但是，费率升高，营业中断保险的价值降低(推论1，图3和4，命题1)。

(3)供应链合作和营业中断保险的应用相互促进。作为投保企业的供应商受益于保险是正常的。但是通过供应链的传递作用未投保的零售商也成了保险的受益者(推论1，图4)，供应商因此也可以减少惩罚支出。这说明了营业中断保险应用到供应链后其价值得到扩展和彰显。保险公司借此可以得到营销启示——从供应链切入去推广营业中断保险。同时零售商更愿意与投保的供应商合作。因此，供应链合作和营业中断保险的应用得到了相互促进。

虽然本文分析了供需不确定情况下供应链和营业中断保险的相互影响，得到了三方共赢的结果，对保险定价也作出了一定的探索，表明了供应链与保险的结合是互利的，但是本文的研究是在需求服从均匀分布的背景下进行的。现实中，需求的分布更为复杂。本文进行研究时采用了英国的保险模式——营业中断保险可以单独投保。而在美国和中国，营业中断保险是财产保险的附加险,财产保险也需要被刻画。此外，本文考察的是批发价契约，为在其他契约下研究供应链与营业中断保险的结合打下了基础。进一步的研究可以考虑一般的需求分布；然后也可以尝试把财产保险和营业中断保险放在一起研究；当然，营业中断保险在其他契约下对供应链的影响也非常值得进一步的研究。

[1] Norrman A, Jansson U. Ericsson’s proactive supply chain risk management approach after a serious sub-supplier accident [J]. Physical Distribution Logist, 2004, 34(5):434-456.

[2] 网易财经.汶川地震保险赔付总额不到20亿 [EB/OL].http://money.163.com/09/0824/11/5HFROMJ60025 335M.html.

[3] Li Qing, Zheng Shaohui, Joint inventory replenishment and pricing control for systems with uncertain yield and demand[J].Operations Research, 2006, 54(4):696-705.

[4] 于辉, 邓亮, 孙彩虹.供应链应急援助的CVaR模型[J].管理科学学报, 2011, 14(6): 68-75.

[5] Yang Zhibin, Aydin G, Babich V, et al. Supply disruptions, asymmetric information, and a backup production option[J]. Management Science, 2009, 55(2): 192-209.

[6] 李彬, 季建华，王文利. 基于应急期权的供应链鲁棒订货设计[J].系统管理学报,2015,24(6): 897-903.

[7] 徐常梅.营业中断保险学[M].上海:复旦大学出版社,2007.

[8] 毛小玉.中外营业中断保险(BIC)扩展责任的比较[J].上海保险, 2003,(1): 18-19.

[9] Rose A, Oladosu G,Liao Shuyi. Business interruption impacts of a terrorist attack on the electric power system of Los Angeles: Customer resilience to a total block out [J].Risk Analysis, 2007,27(3):513-531.

[10] Durukal E, Erdik M. Physical and economic losses sustained by the industry in the 1999 Kocael Turkey earthquake[J]. Nat Hazards,2008,46(2):153-178.

[11] Hartwig R P. Florida case study: Economic impacts of business closures in hurricane prone counties[R]. Wroking Paper， Insurance Information Institute, 2002.

[12] Dong Lingxiu, Tomlin B. Managing disruption risk: The interplay between operations and insurance [J].Management Science, 2012, 58(10):1898-1915.

[13] 蔡鹏.基于营业中断保险的供应风险控制研究[D].上海:上海交通大学,2013.

[14] 赵锦晓.基于营业中断保险的供应链风险管理策略研究[D].上海:上海交通大学,2013.

[15] 戢妍.基于云保险机制的云服务供应链契约设计与策略研究[D].天津:南开大学,2014.

[16] Adams III AF. When a simple analysis won’t do: Applying economic principles in a lost profits case[J].The Value Examiner, 2008,(6): 22-28.

[17] 舒磊,吴锋. 不可靠供应下的风险厌恶采购单阶段模型[J]. 系统管理学报,2015,24(4):602-609.

[18] 米俊毅,匡海波,余方平,等. 我国货运保险对现代物流业促进效用研究[J]. 管理评论,2015,27(9):201-212.

[19] 秦绪伟,杨玉佩,康万根,等. 面向关键设备维修服务的PBC合同与营业中断险集成设计模型及分析[J]. 中国管理科学,2016,24(11):19-28.

[20] 李果,张祥,马士华,等.不确定交货条件下供应链装配系统订货优化与协调研究综述[J].计算机集成制造系统,2012,18(2):369-380.

[21] 杨宝华.营业中断险:业务持续管理与保险产品创新的契合[J].华东经济管理,2011,25(2): 49-52.

[22] 陶存文,耿宇亭.国外营业中断保险制度及其启示[J].保险研究,2008,(4): 6-10.

[23] Kliger D, Levikson B. Pricing insurance contracts-an economic viewpoint[J].Insurance: Mathematics and Economics,1998,22(3): 243-249.