面向高维数据的凹型自表示特征选择方法

朱国荣，冯 昊，叶玲节

（国网浙江省电力有限公司经济技术研究院，杭州 310008）

0 引言

随着电子传感器和网络的蓬勃发展，大量高维数据涌现[1]，不仅增加了进程时间和空间复杂度，且其伴随的维数灾难严重影响了聚类和分类性能[2]。特征选择不仅可以有效去除非相关和冗余特征，降低计算和存储成本，也能有效增强分类、聚类等机器学习模型的泛化能力[3-4]。近年来，许多研究都致力于开发新的特征选择算法[5-8]。

一般来说，特征选择方法根据有无标签可以分为2类：有监督特征选择和无监督特征选择。随着网络和社交媒体的广泛使用，产生了大量无标记数据，因此无监督的特征学习引起了更多的关注。

无监督的特征学习方法可以大致分为3类：过滤式模型、包裹式模型和嵌入式模型。过滤式模型通过如数据统计属性等评价标准选择相应特征子集[7]。包裹式模型可以进行大规模的密集计算[9-10]。嵌入式模型在学习模型中加入选择过程，发现显著特征的同时学习最优分类器[11]。早期的无监督特征选择主要使用一些评价指标来搜索每个特征或特征子集的重要性。这些评价指标包括聚类性能、冗余度、样本相似性、流形结构以及拉普拉斯分数[5]、方差[3]和跟踪比[12]等典型指标。而基于搜索的算法需要高昂的计算代价，为了减少计算，文献[13]提出了一种非搜索式特征聚类方法，依据特征相似度挖掘显著性特征。为更好地保存样本的相似性，一系列基于谱聚类的特征选择方法被提出[14-16]。近年来，朱等人提出一种基于正则化自表示方法的无监督特征选择，将任意特征表示为其他特征的线性组合，通过最小化自表示误差，可以学习一个特征权重矩阵，进而选择特定特征子集[17]。

稀疏正则化通常被用于维数约简和特征选择，并且取得了良好效果。通过引入l1范数正则项，l1-SVM被用于特征选择[18]。通过对特征选择建立损失最小化问题模型，具有组稀疏性质的l2，1范数也被用来消除特征中的冗余[4，19-20]。朱等人将l2，1范数用于约束特征权值矩阵和自表示误差，获得了较好的效果[17]。

在此使用l2，p范数约束特征权值矩阵，其中0≤p＜1。类似于向量l1范数与lp范数的情况，当0＜p＜1时，表示系数矩阵的非零行将会比标准的l2，1范数约束时更少。为了进一步增强系数矩阵的稀疏性，将考虑p=0的极限情况，其正则项为l2，0范数约束。同时，为了消除离群点带来的负面影响，使用标准的l2，1范数来约束损失项。使用一种改进的IRLS（迭代重加最小二乘法）算法求解0＜p＜1时的模型并保证其收敛[17]。而p=0时模型是非凸的且不可微的，无法使用IRLS方法求解，因此，利用ALM（增广拉格朗日法）求解该问题[21]，确保迭代算法为局部收敛。通过真实数据集的实验，表明所提模型比标准的l2，1范数正则化和其他流行的特征选择方法在分类和聚类性能具有更突出的优势。

1 凹型正则化自表示特征模型

1.1 问题描述

现实数据集通常具有许多冗余离群点。一个高效无监督特征选择算法，需要从给定的无标签数据集中，选择一个可以有效描述数据集属性和结构的特征子集。

给定数据集X∈Rm×n，其中m是样本数，n是特征维数。使用fi∈Rm来表示X的第i个特征向量，令X=[f1，…，fi，…，fn]。常见方法都使用样本相似性或流形结构构造系数矩阵，因此，特征选择可表示为多输出回归问题：

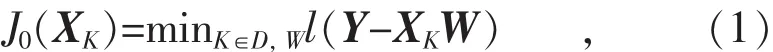
式中：D={1，2，…，n}表示维度；K是选定的子集；XK是X对应的K列；W是对应的特征权值矩阵；l（·）是损失项，用于评估特征选择的性能。

式中：l（Y-XW）是损失项；新引入的R（W）是正则项；λ是正则项参数，帮助动态选择最优特征子集，并选择和计算最优的权值矩阵。

1.2 损失项和正则项

受样本自表示模型的启发[17]，利用特征自表示的性质实现特征选择。类似RSR[17]，使用原数据矩阵X作为字典矩阵，即Y=X，每个特征都可以用所有其他特征线性表示，假设fi是X中第i个特征，则其可以表示为：式中：Wji是权值矩阵W中第j行第i列元素；bi∈Rm是偏移量。

集聚所有特征向量可得：

式中： B=[b1， b2， …， bn]∈Rm×n。

在此模型中，使用特征学习权值矩阵W衡量在偏移量很小时不同特征的重要性。令W=[，…，，其中wi是矩阵W的第i行。||wi||2可以代表自表示模型中第i个特征的重要程度。如果第i个特征对特征表示模型最小化没有贡献度，则||wi||2=0；相反，若第i个特征的贡献度很大，则||wi||2的值也会变大。显然，行稀疏是权值矩阵W这种性质的理想状态。

根据稀疏表示模型，l0范数可以保证稀疏性，但其是非凸的。l1范数在一定条件下等价于l0范数[22]，故通常作为l0范数的凸型替代。文献[23]指出0＜p＜1的lp范数比l1范数更接近l0范数且更具稀疏性。为保证权值矩阵W在行上更具有稀疏性，选择l2，p范数作为正则项约束，并采用p=0与0＜p＜1 两种形式。

对于0＜p＜1的情况，可定义一个正则项形式R（·）=||·。 对于 p=0 的情况，正则化形式为

pR0||·||2，0。 为减缓对离群点的敏感度， 使用 l2，1范数作为约束误差，定义为l（·）=|·|||2，1，通过上述形式定义，可以得到2个目标函数：

式中：λ是非负平衡系数。

l2，p范数的形式定义为：

l2，0范数可以表示为：

式中：δ（x）是逻辑判断函数，表示式见式（9）。

2 优化和算法

本部分描述了模型的优化过程。当p＜1时，目标函数非凸，必须使用迭代方法进行优化。使用IRLS方法可以有效优化0＜p＜1情况下的目标函数，而且可以确定局部最优。对于p=0的情况则利用增广拉格朗日法求解，同时得以保证局部收敛。

2.1 迭代重加权最小二乘法求解l2，p模型

如上所述，式（5）是凹约束问题，可使用迭代重加权最小二乘法求解。根据IRLS算法，给定一个当前权值矩阵Wt，则对角权值矩阵和可以被定义为：

式（12）是关于W的二次函数，将其导数置0很容易得到闭式解：

因此Wt+1的解可以表示为：

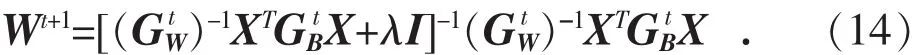
为提升最优解的稳定性，定义了一个足够小的非负值ε：

获得W的最优解之后，根据w值的大小顺序选择包含前k个特征的非零子集，该方法同样可用于式（6）。对于式（5）的解法见算法1。

算法1：IRLS求解0＜p＜1时的凹型RSR模型。

输入： 数据矩阵X∈Rm×n， λ＞0， 最大迭代次数TN。

输出：特征权值矩阵W。

（1）初始化W；

（2）迭代次数T=1；

（5）利用式（14）求解Wt+1；

（6）检查T≥TN是否满足，若是，则终止算法；否则，令T=T+1，算法循环至第3步继续进行。

2.2 增广拉格朗日方法求解l2，0模型

如前文所述，当p=0时，l2，0范数可以更好地提升目标变量的稀疏性，而l2，0范数是一种不可微且极度非凸的优化问题，不能直接使用IRLS。本节使用增广拉格朗日方法求解此问题。

根据拉格朗日法则，引入辅助变量V和E，式（6）可以被重写为：

式中：μ是1个正标量，可以提升迭代速度；Π1，Π2是2个拉格朗日算子，可以随着样本集的变化而变化。式（14）包括3个变量E，W和V，固定其他2个变量交替更新1个变量，最终可以获得模型的最优解。

为求解E，式（14）可以改写为：

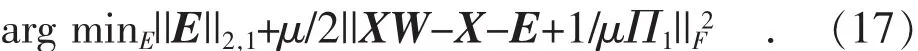
令Y=XW-X+1/μΠ1， 将式（17）写为行向量形式：

根据文献[25]，该子问题具有闭式解：

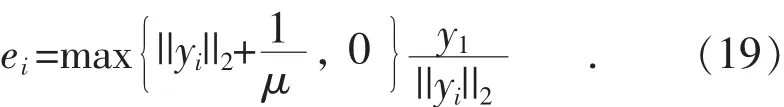
为求解W，式（16）可以改写为如下子问题：

式（20）是一个二次规划问题，具有最优闭式解：

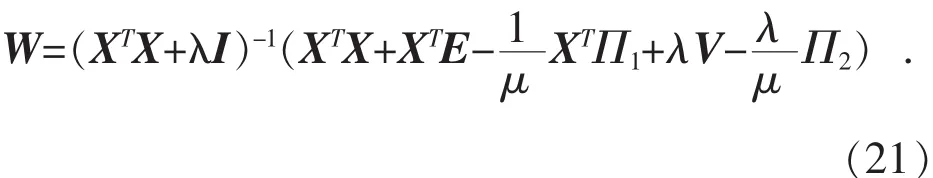
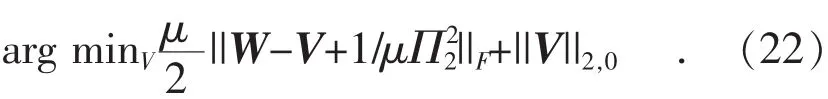
类似对E的求解，令Z=W+1/μΠ2，将式（22）改写成行向量形式：

为求解V，式（16）可以改写为如下子问题：

根据文献[26]，式（23）具有如下闭式解：

式（24）只是高维向量空间中一种硬阈值算子，类似于vi是标量的情况。值得一提的是，如果将式（24）作为一个具体的正则化函数：

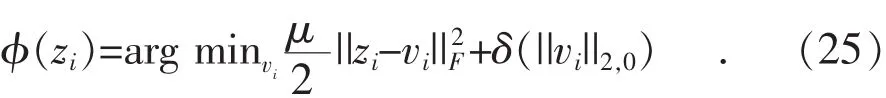
则其具有如下性质：

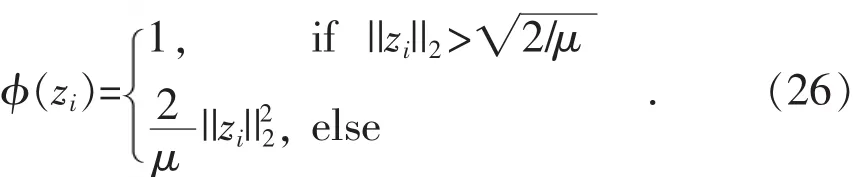
该函数是文献[27]中一维向量在欧几里得距离上的自然扩展。当趋于无穷时，式（26）会收敛于式（9），因此，可以使用正则化函数式（26）作为l2，0范数约束。对于式（16）的最后2项除却Π2可以近似为φ（wi）。实际上，Π2的目的是为了加快收敛速度，因此可以使用 φ（wi）作为式（16）最后两项的正则项。 如此意味着，式（16）是l2，1范数损失项与近似l2，0范数正则项的联合优化，且在迭代过程中稀疏约束会持续增强，近似形式的l2，0范数会逐步接近其实质形式。

综上所述，对于式（6）的解法如下算法2所描述。

算法2：ALM求解p=0时的凹型RSR模型。

输入： 数据矩阵X∈Rm×n， λ＞0， μτ， 最大迭代次数TN。

输出：特征权值矩阵W。

（1）初始化W， Π1， Π2， μ；

（2）迭代次数T=1；

（3）利用式（22）求解Vt+1；

（4）利用式（17）求解Et+1；

（5）利用式（19）求解Wt+1；

（8）μ=μ×μτ；

（9）检查T≥TN是否满足，若是，则终止算法；否则，令T=T+1，算法循环至第3步继续进行。

3 试验

为验证以上所提出的凹型约束特征选择方法，将算法应用在7个公开数据库：orlraws，pixraw，warPIE，TOX， Prostate，Carcinoma[28]和 LUNG[29]。所有数据集的特征数在2 400～11 340之间，且归一化为N（0，1）分布。表1给出了7个数据集的详细信息。将凹型自表示特征选择的2种形式与标准l2，1RSR算法以及5种典型的无监督特征选择方法：Laplacian score[5]，UDFS[7]，SPEC[14]和FSFS[13]做对比。同时，为了检验该算法性能的广泛意义，所有方法在分类与聚类2种任务下进行对比。

表1 测试数据集汇总描述

试验将检验此算法当p=[0，0.4，0.6，0.8]时的算法性能。对于Laplacian score和UDFS，设置所有数据集的邻域数k=5。UDFS和l2，1RSR的正则项参数通过搜索优选。Laplacian score和SPFS中高斯核函数宽度参数也经过遍历搜索。为了公平对比，所有正则项参数和宽度参数都在{0.001,0.005，0.01，0.05，0.1，0.5，1，5，10，100}中选取使算法性能最优的参数。考虑到所提算法的稀疏性，当特征选择数较少时，算法的优势才能被体现。因此，特征选择的数目在{10，15，20，25，30}中进行优选。为量化算法性能，使用2种性能指标：ACC（分类精度）和NMI（聚类归一化互信息）。

表2 分性精度性能对比

表3 聚类NMI性能对比

3.1 分类性能

所有算法的分类精度（%）如表2所示，所有数值都是通过10次运行的平均值，其中在同条件下最高值由黑斜表示，次高值由黑体表示，第3值则采用下划线表示。从表2可以看出，此提算法相比l2，1RSR和其他对比算法，在多数情况下具有突出的性能优势。在部分数据集中，如TOX和Carcinoma，虽然所提算法没有取得最优的精度值，但依然占据着同类算法中的次高值以及第3值。同时，在一些数据集上，稀疏设置具有优异的表现，尤其是p趋于0值时，其在LUNG和Prostate等数据集上具有绝对的优势。

3.2 聚类性能

选中特征子集后，试验使用kmeans方法完成最终聚类。表3给出了所有算法在不同数据集上10次运行的NMI平均值。从中可见，此算法在所有数据集中的聚类结果都优于其他对比算法，其中pixraw数据集中占据了前3个最优值，进一步验证了凹型约束的优越性。

4 结语

提出了一种面向高维数据的凹型自表示特征选择方法。基于自表示性质与lp范数约束增强稀疏性，所提无监督特征选择模型采用l2，p范数约束。当0＜p＜1时，函数变成非凸优化问题，采用IRLS算法进行有效求解。当p=0时，则使用增广拉格朗方法求解l2，0范数约束问题。在7个数据集与标准l2，1RSR和现存流行算法的对比试验表明，所提算法具有明显的性能优势。未来将研究其他形式的凹型约束，并将此处所提模型扩展到有监督特征选择。