基于分段非线性函数的无功补偿经济性模型研究

张文军， 唐 鸣， 何 鹤， 吴 颖

（1.国网浙江省电力有限公司，杭州 310007；2.国网浙江省电力有限公司杭州供电公司，杭州 310009）

0 引言

按照《功率因数调整电费办法》（[83]水电财字215号）的相关要求，电网公司对容量在100 kVA及以上各类客户的功率因数进行考核，奖优罚劣，以促使企业按有关标准设计和安装无功补偿设备，加强无功管理，提高企业用电功率因数。然而，部分用户由于缺乏无功管理意识以及无功补偿设备设计使用不合理等原因，无功电量占比依然过高，产生较高的力率调整电费，增加了企业用电成本。

目前，国内外对于无功补偿的经济性研究多为简单的理论推导，并未考虑用户计量方式的差异以及电网公司考核标准对经济性造成的影响。如文献[1-10]仅对无功补偿的相关技术进行了研究，文献[11]仅对无功补偿容量以及经济性进行了简单的表述。

以下在相关研究成果[12-23]的基础上，综合考虑用户计量方式的差异、电网公司功率因数计算参数和考核标准，推导基于用户实际计算参数的无功补偿容量，并对考核标准进行函数拟合，最终建立用户无功补偿经济性模型。

1 功率因数调整电费表的函数拟合

当前，在计算用户力率调整电费时，主要根据用户功率因数，查询《国家物价局功率因数调整电费办法》中“功率因数调整电费表”对应的百分数（调整系数M）增减电费，这种查表的方式不利于参与各类计算。为此，需通过函数拟合，将上述各表转化成相应的计算公式。

1.1 低于考核标准时的函数

当用户功率因数低于考核标准时，调整系数M为正（惩罚性质，缴纳力率调整电费），调整系数M的计算方法为：

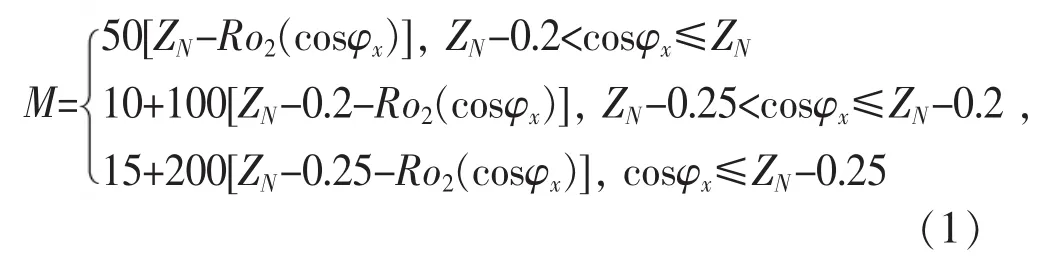
1.2 高于考核标准时的函数

当用户功率因数高于考核标准时，调整系数M为负（奖励性质，减免力率调整电费），不同考核标准下的调整系数M的计算方法为：

力率调整电费RM可表示为：

式中：R为参与力率调整电费计算的电费；R电度为当月目录电度电费；R基本为当月基本电费。

2 不同计量方式下的无功补偿容量

根据文献[4]中无功补偿容量计算方法，结合用户实际已有相关参数，若用户每月的有功电量是稳定的，该用户功率因数为Zx，低于考核标准ZN。

对于高供低计用户，若需将功率因数提高至ZN，需补偿无功容电量为：

式中：ΔQ为需补偿的无功电量；PJ为用户计量装置计量的有功电量；P0为变压器的有功空载损耗功率；k为变压器有功损耗系数；Zx为用户当前功率因数值；Qx为用户在当前功率因数下的无功电量；QN为用户功率因数达到考核标准时的无功电量。

对于高供高计用户，若需将功率因数提高至ZN，需补偿无功电量为：

假设企业1天用电时间为12 h，则需补偿的无功容量可表示为：

式中：D为当月的天数；Δq为需补偿的无功容量。

3 无功补偿经济性模型

无功补偿目标值一般为功率因数考核标准值，但当用户功率因数高于考核标准值时，将被奖励调整电费，因此当用户投资无功补偿设备经济性最佳时，用户无功补偿目标值可能大于考核标准值。

3.1 补偿目标为考核标准值

对于电力用户，无功补偿的最佳选择点为低压侧。为方便计算，取低压无源无功补偿装置的市场价格10 000元/100 kvar，将功率因数提高至考核标准值所需装设的无功补偿装置成本为：

根据相关规定[21]，2015年1月1日后新增的110 kV以下的配电设备折旧年限为15～22年；自动化设备及仪器仪表折旧年限为8年，残值均按5%计算。考虑到无功补偿装置含自动投切控制装置以及测算的保守性，将无功补偿装置按照8年（96个月）年限进行折旧，以设备价值的0.5倍

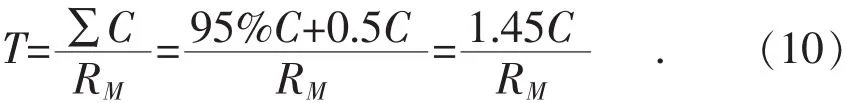
可见，若T＜96，则装设无功补偿设备后，在设备自然寿命结束前即可收回所有投资成本，因此投资方案经济可行。投资期内收益：

3.2 补偿目标超过考核标准值

若功率因数提高至考核标准值以上时，按照功率因数考核相关规定，用户将被奖励力率调整电费，但此时调整系数M较小，投资是否值得需进一步测算。若目标功率因数为Zs（大于考核标准值），则功率因数在提高至考核标准ZN后，继续提高至Zs时：

对于高供低计用户，需补偿无功电量：

对于高供高计用户，需补偿无功电量：

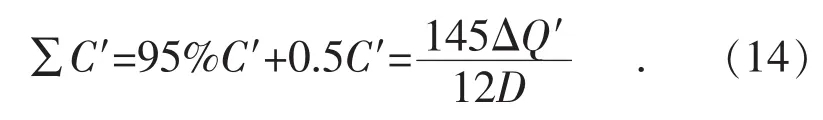
需投入投资金额：作为无功补偿装置后期维护费用，投资回报周期可表示为∶

若用户装设无功补偿装置更为经济，则应满足8年内预计奖励的力率调整电费大于总投资金额，即继续投资的收益大于零：

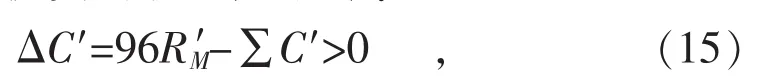
式中：ΔC′为用户将功率因数从ZN提高至Zs时能够获得的投资收益；为用户功率因数从ZN继续提高至Zs时奖励的力率调整电费。

从调整系数M表达式（1）—（4）可知，当功率因数超过相应限值Zm后，M将不再增大，即奖励的力率调整电费不再随功率因数的增加而增加，因此初步判断目标功率因数Zs经济区间为（ZN，Zm]，根据调整系数M表达式，Zm与ZN的对应关系如表1所示。

表1 不同考核标准下的Zm值

M的表达式中包含四舍五入处理，是非连续函数，为方便处理，在代入计算时，先不考虑四舍五入，这样函数在计算极值等过程中可简化为连续函数，待完成计算确定各项取值时，再根据M表达式含四舍五入的特性，调整取值，得到最优解。 将公式（1）—（5）和（12）—（14）代入公式（15），可得到以目标功率因数Zs为自变量的函数不等式，经整理简化后如公式（16）所示：

表2 不同计量方式下各参数值的关系

（1）若不等式在自变量区间内无解，说明用户在装设无功补偿装置时，目标功率因数Zs应设置为考核标准值ZN，超过ZN后继续装设无功补偿装置或增加无功补偿容量在经济上不可行。此时，无功补偿装置的无功容量应选择：

投资期内总收益：

（2）若不等式在自变量区间内存在解空间，说明用户在装设无功补偿装置时，目标功率因数Zs的设置理论上可超过考核标准值ZN，且目标功率因数Zs的最佳选择为解空间内使ΔC′最大的值。

此时，用户功率因数从Zx提高至Zs时，无功补偿装置的无功容量应选择：

投资期内总收益：

4 案例

以某包装印刷有限公司为例，用户相关参数如表3所示。

表3 用户参数

根据公式可得：

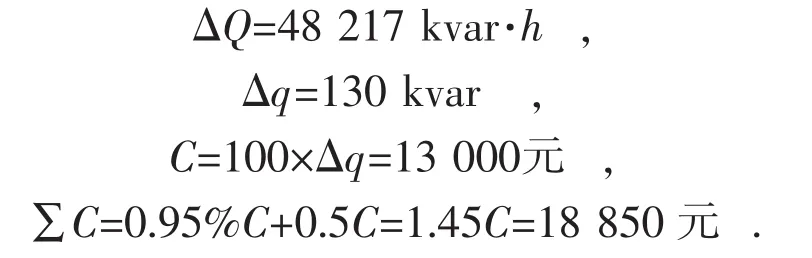
投资回报周期：

可见该用户装设容量为130 kvar的无功补偿装置，即可将功率因数提高至0.9，从而避免缴纳力率考核电费，且不超过3个月即可收回成本，预计企业8年可节省成本约60.6万元，显然，装设无功补偿装置是更为经济的方案。

当功率因数达到0.9后，若继续补偿则有：

ΔC′为关于Zs的函数， ΔC′在Zs的经济区间（0.9，0.955）的函数图形如图1所示。

图1 ΔC′在经济区间（0.9，0.955）的曲线

由于该自变量区间较小，故ΔC′在该区间内图形接近直线且单调递增，显然在满足ΔC′取得最大值的前提下，若Zs最小，所需补偿无功容量也最小，此时的Zs即是最优选择。根据图1，ΔC′在经济区间内是单调递增函数，可见当Zs=0.95，ΔC′最大。

接下来根据M四舍五入的特性判断Zs的最小值。考虑到经过四舍五入处理后，Zs在区间[0.945，0.95]内值都是相等的， 又由于∑C′是单调递增函数，故在保证ΔC′取得最大值的前提下，Zs最小可取0.945。此时：

因此，该用户在装设无功补偿装置时，可将补偿功率因数目标设置为0.945，无功补偿装置容量需235 kvar，并且4个月即可收回全部投资成本，投资期内总收益可达65万元，投资经济效益可观。

5 结论

综合考虑用户计量方式的差异、电网公司功率因数计算参数和考核标准，推导基于用户实际计算参数的无功补偿容量，并对考核标准进行函数拟合，最终建立用户无功补偿经济性模型，最后通过实际案例对模型进行计算演示与验证，以此为用户合理投资无功补偿装置，降低用电成本提供参考。