运用几何直观方法 类比解答同类问题

许芸

在解决问题当中，我们经常发现面对复杂多变的问题情境，学生无从下手胡乱解答的情况。

比如人教版五上“出租车中的分段计费问题”，有这样一道题：

下面是某市出租车的收费标准。（不足1小时按1小时计算）

李叔叔打车从家到单位一共行驶11.2km，算算李叔叔一共要付多少钱？

这道题跟课本例题一样，都是出租车情境，只是由二段计费拓展到三段计费。学生的错误率就非常高，常见错误如下图：

错误原因是第二段的行驶路程弄错，本质是缺乏几何直观的抓手，对每段的分段数量不清楚。

还比如在学习用公因数和公倍数解决问题当中，很多学生容易弄混这两种不同的类型，比如在人教版数学书81页练习十二中的这道习题：

题目应该是求最大公因数，学生却求了最小公倍数，说明学生没有理解这类问题的本质。

因此在教学中，如果能够运用一定的手段对此类问题进行沟通，如建构直观形象的几何模型，使学生有解决问题的方法，就能提高学生解决问题的能力。

一、引入方法，帮助审题

几何直观有利于把复杂的数学问题变得简单、形象，特别在问题的数学化表征中有着很大的作用。在常规的教学中我们应鼓励学生进行多样化的信息表征，然后进行优化，最后凸显几何直观表达信息的优越性。建立几何直观模型，是为审题搭建脚手架。

比如这道分段计费问题：

某市按以下规定收取水费：用水量不超过3吨的，每吨收费2.5元；超过3吨不超过10吨的部分，每吨收费3.5元，超过10吨的部分，每吨收费4元。小强家9月份的用水量是12.5吨，应付水费多少钱？

学生用文字、画表格和画线段图等不同方式表征信息。如图：

在确定线段图是最简单、形象的表征方式后，教师再追问一句：画表格和画线段这两种方法有什么共同的地方？然后将两幅图叠在一起（如下图），学生发现两者都清晰地表示出了每段的数量和对应的单价，由此学生初步感知了分段计费问题的几何模型。

还比如“用最大公因数解决问题”中的例题，在信息呈现方式中这种画图的方式特别优化，在分析解答中，学生明确问题的本质就是求长和宽的公因数后，再在原先的直观图中抽象出平面数轴图（如下图）。三幅图层层递进，帮助学生对题意本质的理解。

二、妙用方法，明了算理

妙用几何直观，使学生在类比沟通中明了算理。如设计巩固练习题，让学生运用建立的几何直观，掌握同类问题的解题方法。

在“分段计费问题”中可设计一道选择题，如：

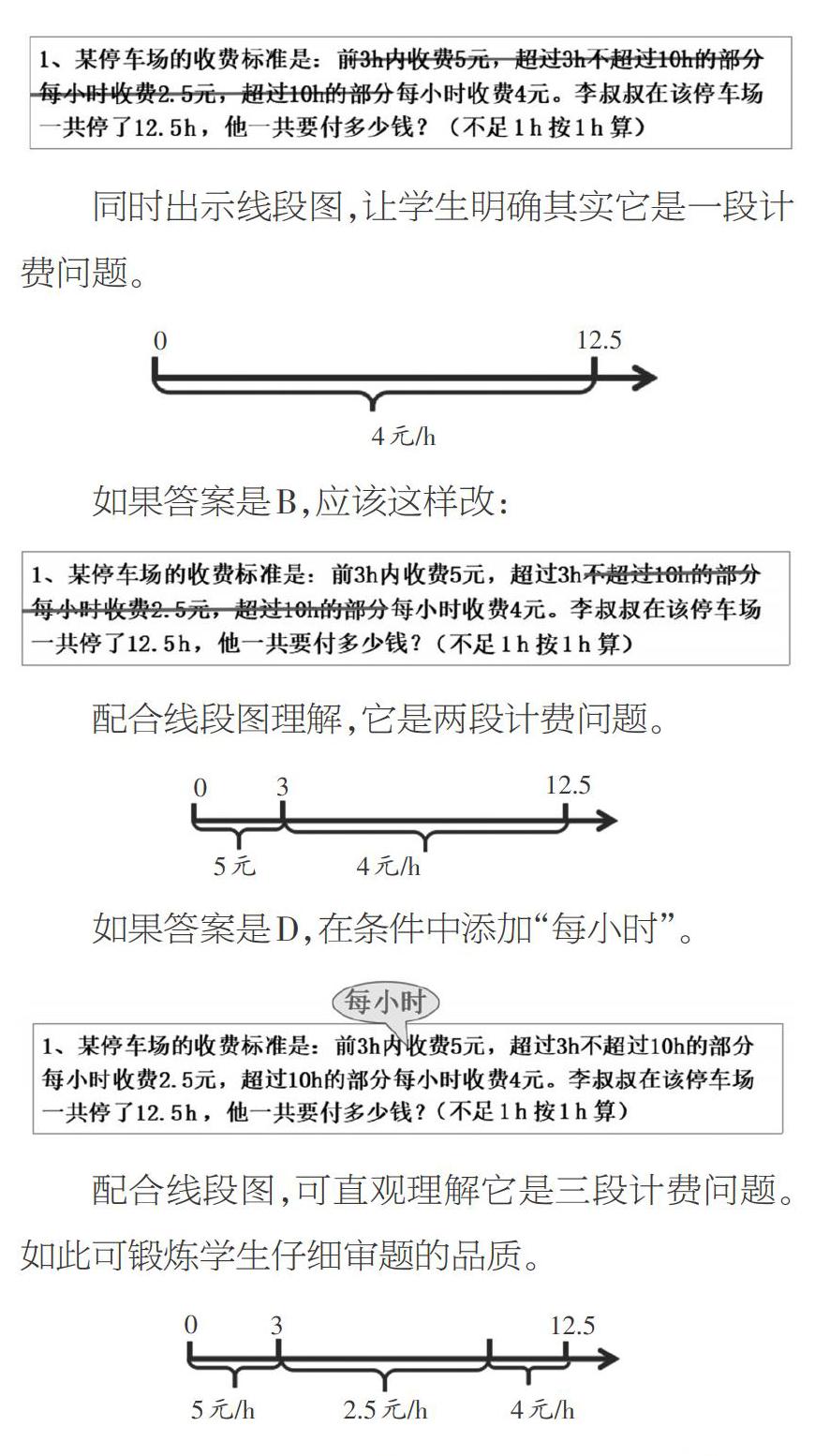
某停车场的收费标准是：前3h内收费5元，超过3h不超过10h的部分每小时收费2.5元，超过10h的部分每小时收费4元。李叔叔的车在该停车场停了12.5h，他一共要付多少钱？（不足1h按1h算）

A. 12.5×4

B. 5+（12.5-3）×4

C. 5+（10-3）×2.5+（12.5-10）×4

D. 3×5+（10-3）×2.5+（12.5-10）×4

此题的正确答案是C，但教师不仅要求学生能找准正确答案，还要求学生能根据錯误的选项改编题目，达到一题多练和逆向运用方法的效果。如果答案是A，题目应该这样改编（划去题目中的条件）：

同时出示线段图，让学生明确其实它是一段计费问题。

如果答案是B，应该这样改：

配合线段图理解，它是两段计费问题。

如果答案是D，在条件中添加“每小时”。

配合线段图，可直观理解它是三段计费问题。如此可锻炼学生仔细审题的品质。

最后将3个线段图合成一幅图，明确不管是一段计费、二段计费还是三段计费问题，都要明确每段的数量和对应的单价，然后将每段的总价加起来。这是解答这类问题的几何模型和方法。

三、活用方法，提升能力

任何模型的建构都是为了灵活广泛地运用。因此教师可以引导学生从深度和广度上灵活运用几何直观方法，进行深层次和多维度的类比沟通，提升学生解决问题的能力。

比如在分段计费问题的提高练习中，可根据这个几何直观模型结构让学生自己尝试着编一道分段计费问题。在课堂中很多学生还突破模型结构，创造出四段、五段的计费问题和逆向思维的题目（如下图），深刻体现出对几何直观模型方法不是僵化地理解，而是灵活地运用。

同样在用公因数解决问题后，教师让学生探讨可以放棱长最大是几分米的正方体纸箱叠满房间的问题。最后通过直观操作，抽象出空间数轴图，并对比之前的平面数轴图，明确这类问题的本质就是求多个数的公因数。

两次课堂实践验证了运用几何直观方法类比沟通解答同类问题的可行性和有效性。在平常的教学中如果能够善用几何直观方法，建立与同类问题的联系，相信会带来更多的惊喜。比如在低段教学中我们经常遇到的里程问题、水电表问题、经过时间问题、看书页数问题等，其实都属于累计计数问题。教师同样可以引导学生运用数轴图几何直观的方法建立联系，提升学生解决同类问题的能力。

小红看一本书，星期一看到43页，星期二看到78页，星期三看到120页，小红星期三一共看了多少页？

运用几何直观方法类比解答同类问题是非常有效的教学方法，它不仅能帮助学生理解分析题目，还能为学生找到同类问题的本质联系建立直观的形象支撑，有助于学生掌握同类问题解答的基本方法。

参考文献：

[1]丁占海 .读 “图”教学：让几何直观自然地生长[J].教学与管理，2013（35）.

[2]麻炳铃 .几何直观——搭起解决问题的脚手架[J].小学教学参考，2016（15）.

[3]朱向明.借助几何直观 积累问题解决经验[J].教学与管理，2013（17）.

[4]蔡杰.运用“几何直观”达成多维目标[J].小学教学参考，2014（5）.

（浙江省杭州市濮家小学 310000）