高中数学实验室对数学教学的影响

马恩荣

【摘 要】本文论述高中数学实验室对教师教学方式、学生学习方式和解题教学三个方面的影响，认为在高中数学教学中适当运用数学实验室的相关数学工具能够较好地帮助教师的教和学生的学，有利于培养学生的探究能力，培养学生数学抽象、数学建模等数学素养，培养和提高学生独立分析问题和解决问题的能力，使新型探究式教学成为可能。

【关键词】高中数学实验室 图形计算器 教学方式 学习方式 解题教学

【中图分类号】G 【文献标识码】A

【文章编号】0450-9889（2017）11B-0028-03

随着信息技术的迅猛发展，以规尺粉笔为主的数学课堂已经无法满足教学需要，以 PPT、图形计算器、几何画板等为代表的教学辅助工具逐步深入课堂，老师的教学手段和学生的学习方式正在经历粉笔到鼠标、笔尖到指尖的革命性变化。2014 年 3 月 15 日，教育部《中小学“数学实验室”建设的研究》开题会在北京召开，会议对高中数学实验室建设标准等问题做了讨论、对研究做了具体规划。各地区也陆续建立有特色的数学实验室，并使用数学实验室进行部分内容的教学。那么，数学实验室环境下信息技术与数学教学的深度融合有哪些促进，高中数学实验室对数学教学究竟有什么影响呢？

一、对教师教学方式的影响

从下面函数图象可视化、概念情景化和数据处理智能化三个案例的实践中可以看到，在高中数学实验室的支持下，数学教学不仅可以采用“演示—讲授”模式（传统教学模式，教师在讲解的过程中，利用投影展示来突出教学重、难点），还可以采用“发现—探究”模式，该模式下，教师是课堂学习情境的创造者、课堂学习活动的组织者，突出以学生为主体，注重学生主动发现问题、解决问题的能力和创造力的培养。在一些数学探究价值较高的内容上，比如对数函数图象和方程曲线问题的探讨、某些结论的发现等，“发现—探究”模式可以培养学生发现问题——提出猜想——验证解决问题的探究意识和思维能力。高中数学实验室拓宽了教学的渠道，让新型探究式教学成为可能。

（一）几类不同增长的函数模型

人教 A 版教科书中几类不同增长的函数模型一节有两个例题，用具体的例子比较了二次函数、指数函数和对数函数的增长情况。在图形计算器技术支持下，教师可以利用图形计算器的图形功能直接画出函数 y=2x，y=x2 和 y=log2x 的图象（如图 1），借助图形计算器图解功能标出函数图象的交点（图形计算器可以标出所有交点），使学生有观察的材料。课堂教学实践表明，学生很容易总结出这三类函数模型的增长特点。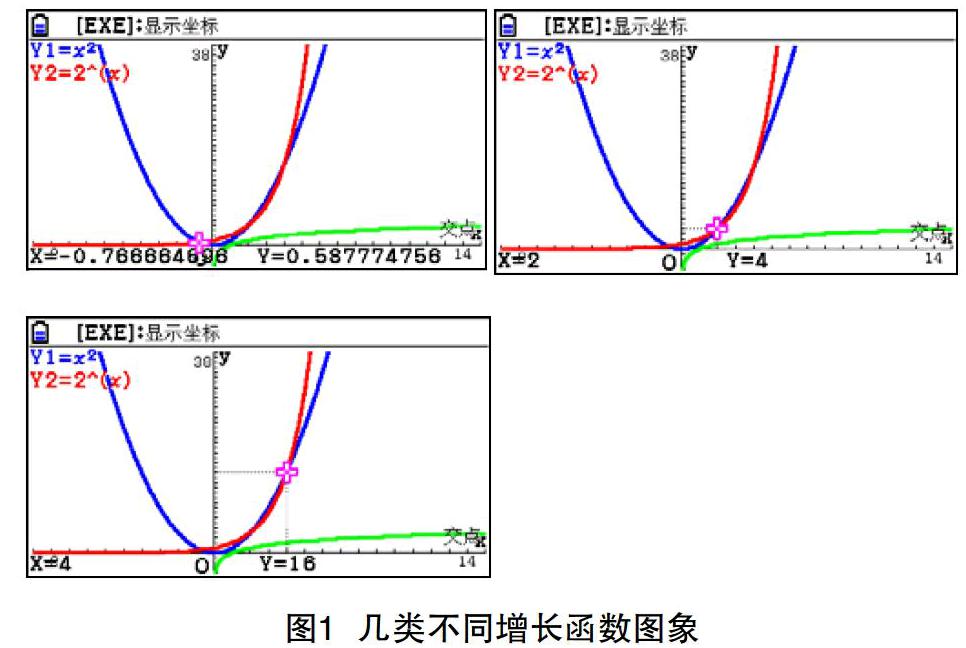

（二）偶函数概念的教学

利用图形计算器可以帮助学生更好地理解偶函数的概念。什么叫作偶函数呢？学生可能会联系到偶数的概念。此时教师可以列举一系列的偶函数，如 y=x-4，y=x-2，y=x0，y=x2，y=x4。从中学生很容易发现这些函数的指数都是偶数。教师（或学生）利用图形计算器做出这些函数的图象（依次如图 2 所示），让学生观察这些图象的共同点。学生不难发现这些函数的图象都是关于 y 轴对称的，而这就是偶函数概念的本质。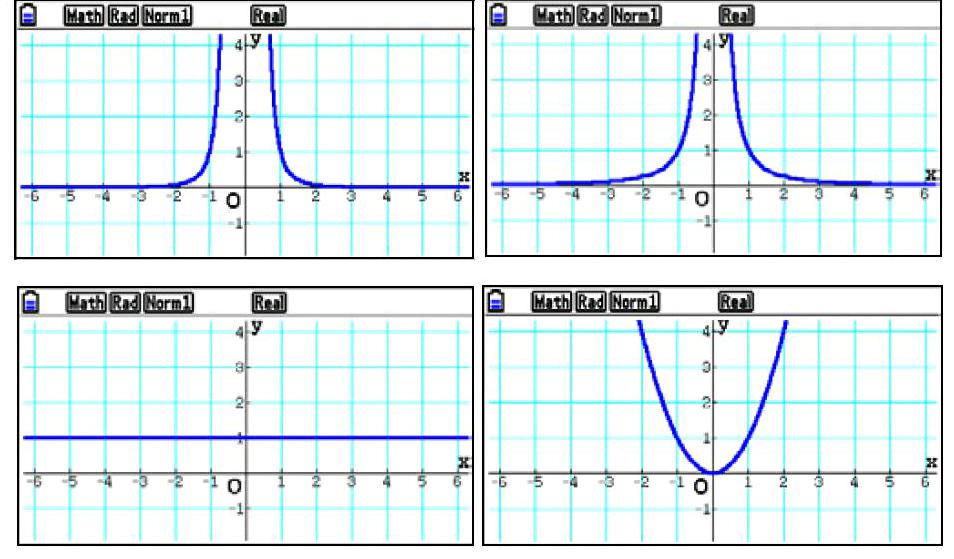

（三）回归分析

《普通高中数学课程标准（实验）》提出，“统计教学必须通过案例来进行”。在线性回归教学的基础上，教师提供具体情境—— 一张桥拱的照片，提问怎样用一个函数来拟合桥拱的形状模式。学生自然会联想到二次函数，但是怎样求得这个用于拟合的二次函数呢？学生不太清楚。此时教师可以借助图形计算器展示整個过程：描点，收集数据，二次回归，绘图观察拟合的效果（见图 3）。经历这一过程，学生对数据处理的全过程以及统计学的基本思想就会有深刻印象，得到更好的理解。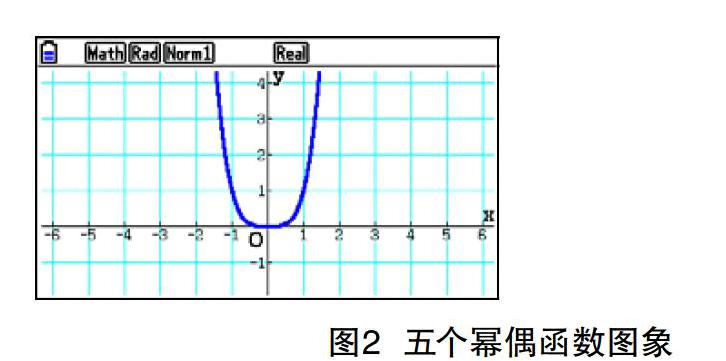

二、对学生学习方式的影响

借助图形计算器和动态几何软件，学生可以动手编制程序模拟随机现象，可以跟踪动点轨迹探究方程曲线，可以计算、作图辅助思考等。高中数学实验室为学生提供自主探究的平台，拓宽学生的学习渠道。一般高中数学探究过程包括观察分析数学事实，提出有意义的数学问题，猜测、探求适当的数学结论或规律，给出解释或证明。高中数学实验室内图形计算器以及几何画板等是学生自主探究的平台，这些技术不仅是学习和探究的工具，而且还可以帮助学生进行思考。在这些技术支持下，学生探究更加直接，学习方式更加丰富有效。

（一）几何概型经典例子——为学生提供自主探究平台

在普通高中人教 A 版必修 3 第 137 页有这样一个经典的几何概型问题：

假设你家订了一份报纸，送报人可能在早上 6：30-7：30 之间把报纸送到你家，你父亲离开家去工作的时间在早上 7：00-8：00 之间，问你父亲离开家前能拿到报纸的概率是多少？

虽然学生或多或少能体会到这是几何概型的问题，但学生并不能很好地解决这个问题，因为他们不明白这里的测度是长度还是面积。如果有图形计算器作为技术支持，那么在这样的情况下，学生就可以写出程序模拟这个过程，得到一个近似的结果。这个近似的结果不仅可以帮助学生思考，而且还有验证的作用。本问题涉及两个随机变量，不妨设为 x 与 y。它们分别在区间[6.5，7.5]和[7，8]内，当 x≤y 时，父亲能拿到报纸。以下是学生编写的程序和运行结果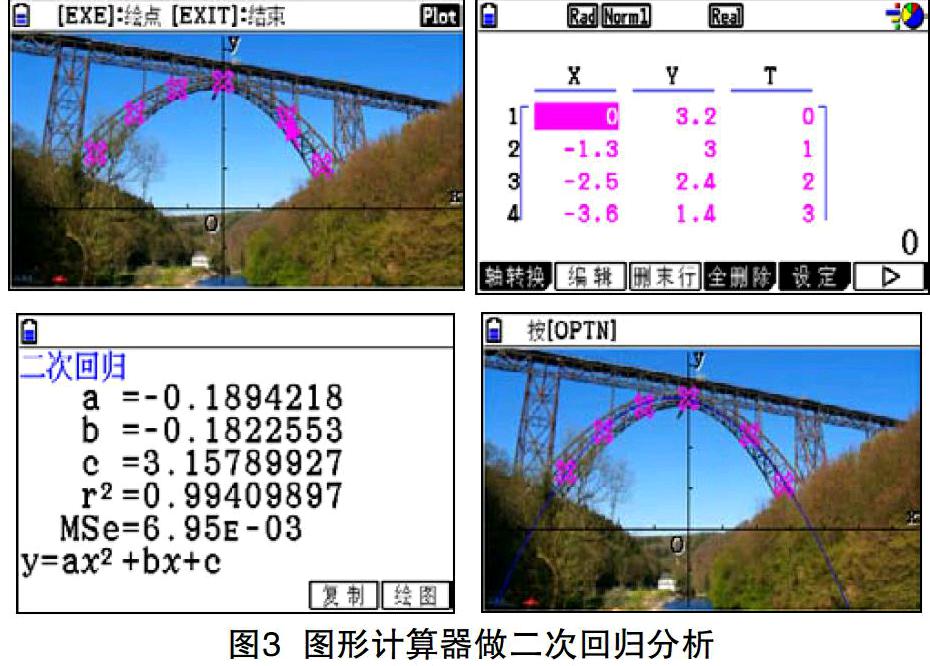：endprint

（二）中点轨迹——辅助理解

对于某些动态轨迹问题，学生可能一时无法判断轨迹是什么，这时他们可以自己动手利用图形计算器或者几何画板软件来跟踪轨迹，辅助理解和判断。

例如，已知定点 D（4，0）和曲线 x2+y2=1 上动点 C，求 CD 中点 E 的轨迹方程。

图形计算器和几何画板软件等均可以完成中点轨迹跟踪，但实践证明，由于图形计算器界面太小且手动作图不够灵敏，故这类问题采用几何画板或超级画板更具优势。以下是利用几何画板做的中点轨迹跟踪，可见中点的轨迹是一个圆，并且圆心的位置和半径的大小均得到一定程度的揭示。此时，学生对这个题目已经有所了解，回过头来求该轨迹的方程时已经有明确的方向，信心十足。

三、对解题教学的影响

在涉及函数图象的一些问题中，数形结合往往可以提供好的解题思路。但不是所有的图象都容易动手画出，这时图形计算器就是一个好帮手。借助图形计算器作图，进行数形结合就可以帮助学生进行思考，开阔思路、缩短思考路径，从而获得好的解题思路。图形计算器的计算功能可以为解题教学（计算繁杂的情况下）争取时间，让教学重点更突出。值得指出的是，图形计算器可以辅助思考，帮助获得解题思路，但并不能提高解题能力。解题中解题回顾尤其重要，只有在解题后对寻求解答的整个思考过程进行梳理才能真正提高解题能力。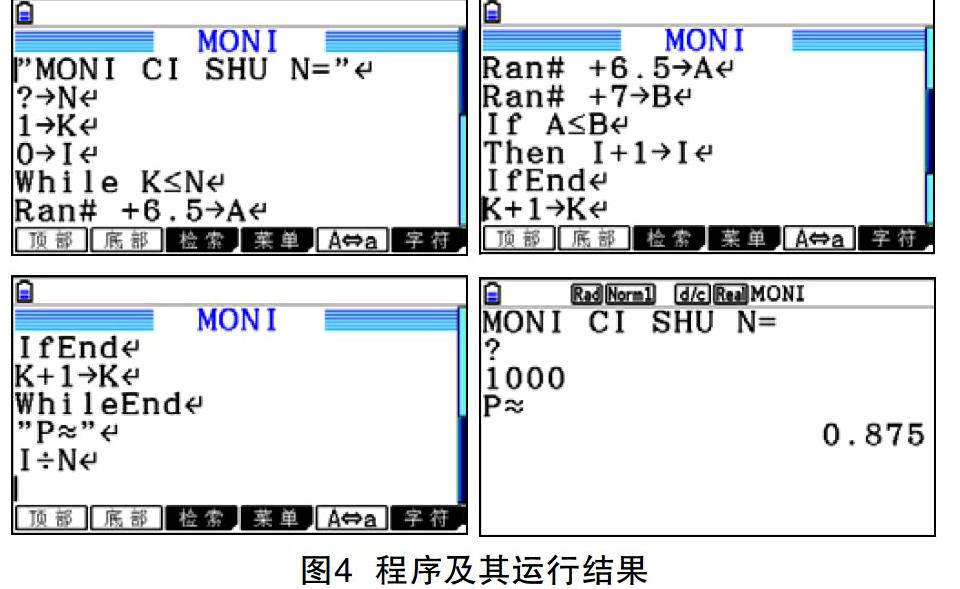

（一）函数应用题——数形结合促进思考

以下这个例题是桂林市 2014—2015 年度上学期高一数学期末考试的压轴题。通过对学生答题情况的分析，发现学生能完成第（1）题，但第（2）题，有的学生没有思路，有的学生证明不严谨。题目如下：

标准答案很简洁，然而学生需要知道的是为什么要这样做。这个解答的想路是怎么来的？有没有其他的解法？

为加深理解，不妨将问题特殊化，令 a=2，借助图计算器作 的图象。画图如下：

在图形函数中输入函数解析式，画出图象后利用图解功能标出函数零点。由图可知，函数图象分为两部分，左部在横轴上方，右部图象在（-1，+∞）上单调上升，函数只有一个 0 点，且 0 点对应的 x 大于 0 。观察到这些特点，原命题的证明就有了思路，证明分为两部分。一部分证明，当 x<-1 时，f（x）>0，即函数在（-∞，-1）上无 0 点；另一部分，证明当 x>-1 时，函数只有一个 0 点，且该 0 点对应的 x 大于0。于是得到以下证明：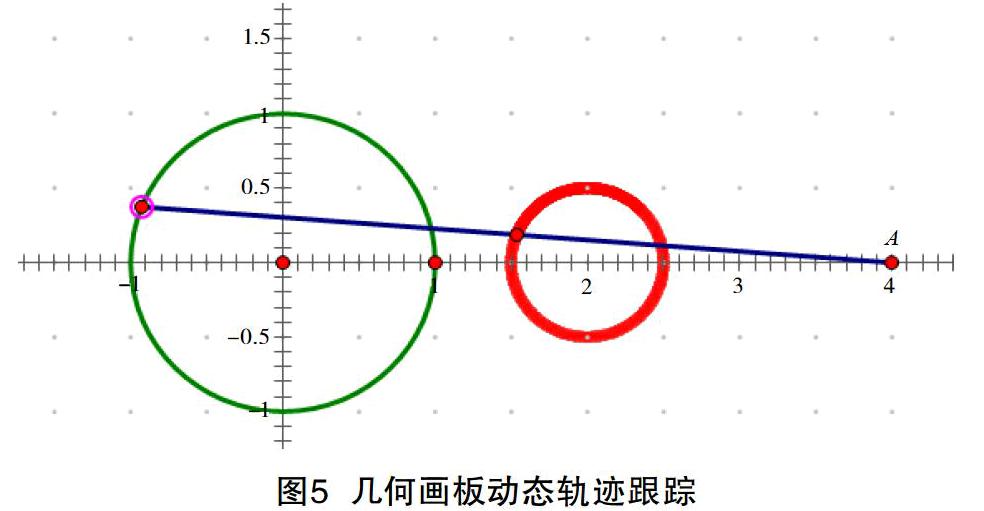

〖证明〗当 x<-1 时，有 ax>0，，故 ，即函数在（-∞，-1）上无 0 点。当 x>-1 时，函数 f（x）在（-1，+∞）上递增，故 f（x）在（-1，+∞）上至多有一个 0 点。考虑到 f（0）=1-2<0， f（2）=a2>0，故函数的唯一 0 点在（0，2）内。

综上，函数 f（x）无负的零点，即方程 f（x）=0无负根。

（二）独立性检验——强大计算辅助

图形计算器有较强的计算功能，在解题中如果遇到一些繁琐而没必要手算的计算时，可以使用图形计算器。例如，在人教 A 版选修 1-2 独立性检验的基本思想及其初步应用中，独立性检验思想是教学的重点，计算则不是。下面以例 1 来具体说明。

〖例 1〗在某醫院，因为患心脏病而住院的 665 名男性病人中，有 214 人秃顶；而另外 772 名不是因为患心脏病而住院的男性病人中，有 175 人秃顶。判断秃顶与患心脏病有没有关系，能否在犯错误的概率不超过 0.010 的前提下认为秃顶与患心脏病有关系？

〖分析〗根据题目所给数据，得到如下列关联表：

通过简单计算不难发现，秃顶样本中患心脏病的频率明显高于不秃顶样本中患心脏病的频率，因此可以认为秃顶与患心脏病有关系。接下来就是判断能否在犯错误的概率不超过 0.010 的前提下认为秃顶与患心脏病有关系。据数据有：

显然，这个计算思维含量较少，对学生而言较繁杂，并且不是教学的重点，如果利用图形计算器的计算功能来帮助计算那么就十分方便。用图形计算器算得 k=16.373>6.635。因此，在犯错误的概率不超过 0.010 的前提下，认为秃顶与患心脏病有关系。

总之，高中数学实验室可以拓宽教师的教和学生的学的渠道，可以帮助学生思考，让新型探究式教学成为可能，让学生的自主探究有了很好的环境和辅助工具，对发展学生数学抽象、数学建模等数学素养，培养和提高学生独立分析问题和解决问题的能力有着十分重要的作用。

【参考文献】

[1]张 锐.信息技术与数学课程整合的教学模式探讨[J].电化教育研究，2007（12）

[2]中华人民共和国教育部.普通高中数学课程标准（实验）[M].北京：人民教育出版社，2011

（责编 卢建龙）endprint