降雨强度对不同渗透性土质高边坡稳定性数值分析

(湖南省永州市公路局工程处，湖南 永州 425000)

0 引言

近年来，国内的公路、铁路等工程建设得到蓬勃发展，在山坡地区出现较多的边坡工程，当雨季期间雨水频繁入渗，会造成边坡失稳引发滑坡灾害[1]。根据全国地质灾害调查结果可知，滑坡约占总地质灾害的50%左右，其中降雨入渗诱发的滑坡占比45%以上[2,3]。降雨入渗会引起边坡土体内的孔隙水压力增大，导致边坡内基质吸力和黏聚力减小，造成边坡失稳诱发滑坡[4,5]。可见边坡内的孔隙水压力与土体渗透性及降雨强度密切相关，基于此，本文采用有限元分析方法，重点分析不同渗透性的土质边坡分别在3种降雨强度作用下的稳定性，分析结果对土质高边坡的稳定性控制及防护提供理论依据。

1 计算模型

本文使用Geo-Studio有限元软件进行计算分析，其中边坡稳定性采用Slope/w模块，地下水渗流采用Seep/w模块。试验流程首先基于有限元法结合Seep/w做降雨入渗条件下的二维非饱和渗流分析，然后依据极限平衡法运用 Slope/w软件对边坡的稳定性能进行详细分析[6]，具体试验步骤为：①输入非饱和土相关公式、参数；②设定降雨因素，运用Seep/w软件进行渗流分析；③计算边坡的孔隙水压力；④输入边坡几何特征、土壤特性、降雨时间及雨强等参数；⑤计算安全系数及滑动面。

1.1 模型建立

运用Geo-studio有限元软件建立边坡计算模型，边坡模型及其网格划分大致如图1所示，其中蓝色线条表示地下水位，红色线条表示AB截面，整个模型中共1 064个结点，994个单元。边坡模型中各参数如表1所示。

图1 网格划分示意图

表1 边坡模型参数左高层/m左地下水层/m右高层/m右地下水层/m坡顶/m坡底长度/m坡脚/m坡高/m坡角/(°)12 56321232100122035

1.2 材料参数

在边坡渗流分析过程中，需在Seep/w软件中设置渗透系数函数曲线与土水特征曲线2个参数。参考张雪东[7]试验可知，土水分特征曲线可通过体积压力板确定，本次试验采用的土水曲线如图2所示。而渗透系数函数曲线可在饱和渗透系数的基础上，通过Van Genuchten模型计算获得[8]，并分成高、中、低3种渗透性，具体情况如图3所示，其饱和条件下的渗透系数依次为ks=1×10-1cm/s、ks=1×10-3cm/s、ks=1×10-5cm/s。Slope/w边坡稳定分析过程中的各项材料参数如表2所示。另外，本次试验为降雨入渗对非饱和边坡的稳定性影响，因此土壤中存在随土壤含水量增减而变化的剪力强度，故需设置一个随基质吸力ua-uw而变化的内摩擦角φb。

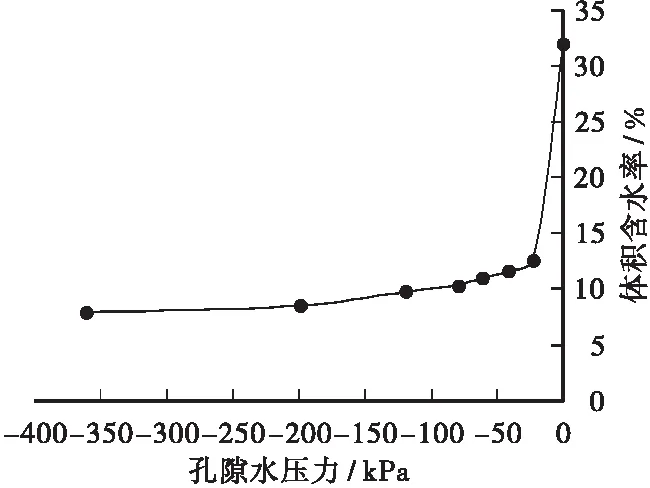
图2 土水特征曲线

图3 渗透系数函数曲线

表2 材料参数容重/(kN·m-3)含水量/%有效粘聚c′/kPa有效内摩φ′/(°)ϕb/(°)19 0911 51228 413 86

1.3 边界条件

边坡左侧有6 m地下水位，右侧有12 m地下水位，故左右两侧以下区域为定水头的边界条件，而以上区域设置为零流量边界；对于边坡的坡面、坡脚以及坡顶的表面区域，由于不存在水流的流入和输出，即水流量为0，故边界条件设置为定流量；坡底区域设为不透水边界，其水流量也是为0，故边界条件与边坡的坡面、坡脚以及坡顶的表面区域一致。上述设定的边界条件为初始状态下边坡地下水水头的分布情况，具体如图4所示，在此基础上针对边坡的稳定性进行暂态模拟。

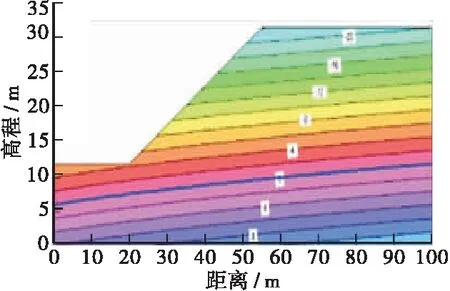
图4 初始状态下边坡地下水压力水头分布

1.4 降雨条件

为了探讨降雨强度和渗透性对边坡稳定性的影响，笔者在降雨持时3 d和雨型均匀的条件下，拟定了渗透系数分别为k1=1×10-1cm/s、k2=1×10-3cm/s、k3=1×10-5cm/s，降雨强度分别为20、40、60 mm/h共9种不同情况，针对不同降雨强度和渗透性下的边坡稳定性展开详细分析，具体情况如表3所示。

表3 各数值情况示意表编号渗透性渗透系数/(cm·s-1)降雨强度/(mm·h-1)11×10-1202高1×10-14031×10-16041×10-3205中1×10-34061×10-36071×10-5208低1×10-54091×10-560

2 边坡稳定性能分析

通过对不同雨强和渗透系数条件下的边坡稳定性进行有限元数值分析，获得各时段边坡的安全系数值如图5～图7所示。其中图5为高渗透性k1=1×10-1cm/s时，不同降雨强度下各时段安全系数的变化曲线，从图5中可以看出，当降雨强度为20 mm/h时，边坡的安全系数在降雨8 h后逐渐缓慢下降，而雨强为40 mm/h和60 mm/h时，边坡的安全系数分别于5 h、4 h后就开始呈下落趋势；但当降雨持续到16 h后，3种雨强下边坡安全系数均达到平缓状态，且大致相同，其因为土质边坡受到降雨入渗的影响，基质吸力不断被消散，从而导致土壤强度逐渐削弱并降至最低值，故后续降雨难以影响边坡的稳定性能。

图5 k1=1×10-1 cm/s不同雨强下安全系数的变化曲线

在高渗透性土壤边坡AB截面中，3种不同降雨强度作用下的孔隙水压力变化情况分别为：降雨强度为20 mm/h时，边坡表层的孔隙水压力随着降雨时间的增长逐渐增大，且增幅较为明显，当降雨持续到8 h后，土壤内的基质吸力开始不断消散，在降雨持续至10 h左右，浅层边坡内的基质吸力基本全部被消散且其安全系数开始逐渐减小，在降雨持续至16 h左右，边坡的孔隙水压力和安全系数均不再受后续降雨的影响而发生变化。降雨强度为40 mm/h时，浅层边坡内土壤的基质吸力在降雨持时5 h后就基本全部消失，其安全系数开始逐渐减小，而当降雨持续至10 h左右，孔隙水压力和安全系数均趋于稳定，且均不受后续降雨的影响。降雨强度为60 mm/h时，边坡表层内孔隙水压力和安全系数的变化情况基本相似，在降雨持时4 h后孔隙水压力不断增加，安全系数则逐渐减小，而在降雨持续8 h后，两者均不再受后续降雨影响。

中渗透性(k2=1×10-3cm/s)、不同降雨强度情况下，土壤边坡的安全系数随降雨持时的变化曲线如图6所示。从图中可以看出边坡内的安全系数随着降雨持时增长逐渐减小，其中雨强为20 mm/h时，边坡内的安全系数在降雨39 h后开始出现明显减小；而雨强为40 mm/h和60 mm/h的曲线变化规律基本一致，其边坡的安全系数均在降雨33 h后才出现明显降幅，这是由于上述2种降雨强度大于模型中设置的渗透系数，故边坡的饱和渗透系数决定其自身入渗的雨水量，又因为渗透系数的相同，使得2种降雨强度下的安全系数变化曲线几乎相同。

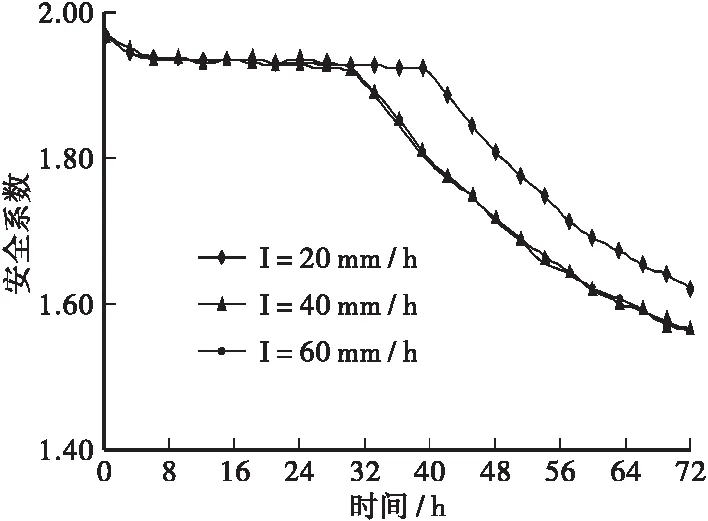
图6 k2=1×10-3 cm/s不同雨强下安全系数的变化曲线

在中渗透性土壤边坡AB截面中，3种不同降雨强度作用下的孔隙水压力变化情况分别为：降雨强度为20 mm/h时，边坡表层的孔隙水压力在初期存在小幅度增大趋势，但降雨3 h后保持了一段时间平稳，直至39 h后边坡孔隙水压力又出现明显增大，同时其安全系数也逐渐减小。降雨强度40、60 mm/h情况下边坡的孔隙水压力随时间变化趋势大致相同，其降雨初期的孔隙水压力与雨强20 mm/h几乎相同，也存在小幅度增大，即表层1 m处的孔隙水压力由负值逐渐增至0，但在降雨3～33 h时段中孔隙水压力不再随降雨时间变化，之后又出现明显上升现象。

低渗透性(k3=1×10-5cm/s)、不同降雨强度情况下，土壤边坡的安全系数随降雨持时的变化曲线见图7。由图7可知，3种降雨强度的安全系数变化曲线均基本相同，且随着降雨时间的增长边坡的安全系数并未有所变化，这是由于土壤的渗透系数较低，基质吸力较强，雨水难以渗入土壤内部，故降雨入渗对边坡稳定性产生的影响并不明显。

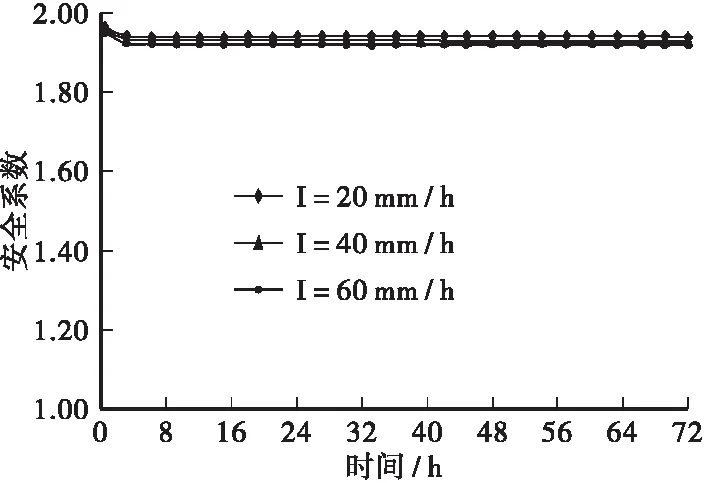
图7 k3=1×10-5 cm/s不同雨强下安全系数的变化曲线

在低渗透性土壤边坡AB截面中，3种不同降雨强度作用下的孔隙水压力变化情况基本相同，且其压力数值均在降雨3 h前由负值增至为0，随着降雨持续至模拟结束，边坡表层处的孔隙水压力均保持一致无任何变化。

综合上述分析结果可知，降雨雨强和渗透性能够影响边坡的稳定性能；渗透系数越低，边坡就越稳定；降雨强度越大，安全系数就越低，边坡的稳定性也会受到不同程度影响。当降雨强度比边坡的入渗率大时，大部分雨水会形成地表径流而流走，只存有一小部分的雨水渗入边坡内部，而此时边坡稳定性也会受到一定程度影响。渗透性决定降雨强度在边坡稳定性中存在一个极值，因此渗透性可作为求取边坡失稳情况下临界雨强的推估条件。

土壤边坡中孔隙水压力和最有可能破坏面的变化关系如图8～图10所示，由于图幅较多，本文仅列出降雨强度20 mm/h不同渗透系数情形下的变化关系图。由图可知，当边坡内无雨水入渗时，最有可能破坏面没有受到任何影响处于稳定状态，属于较深层的滑动面，此时的安全系数也相对较高，具体如图8a、图9a所示；当雨水入渗深度至边坡表层时，其土壤的基质吸力会随着含水量的增加逐渐消散，致使土壤的抗剪强度不断降低，其最有可能破坏面开始变成浅层圆弧状的滑动面，如图8b、图9b所示；随着后续雨水的不断渗入，边坡内最有可能破坏面的圆弧面不断加深，同时也导致安全系数不断的减小，如图8c、图9c所示。但是随着雨水入渗的持续破坏，边坡内的圆弧滑动面并非不断加深，当入渗的雨水达一定程度时，边坡内圆弧滑动面和安全系数均不再发生任何变化，此时受到破坏的圆弧面包含整个雨水入渗部分，如图8c所示。当边坡土层的渗透系数较小时，持续降雨并不会对其孔隙水压力和最有可能破坏面造成影响，如图10所示。

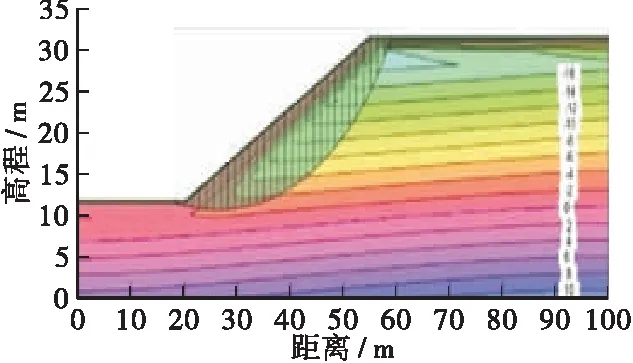
a)T=6 h，FS=1.935

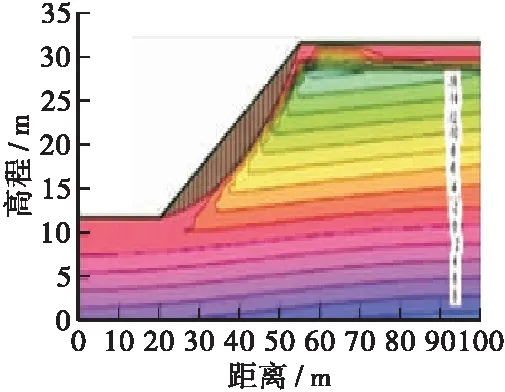
b)T=9 h，FS=1.795

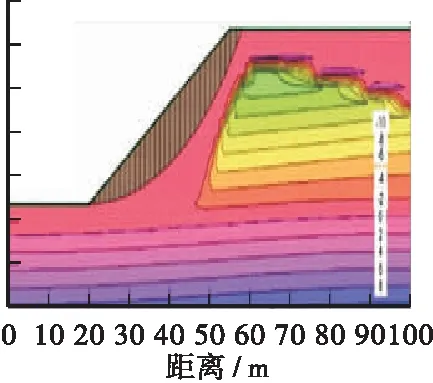
c)T=24 h，FS=1.557

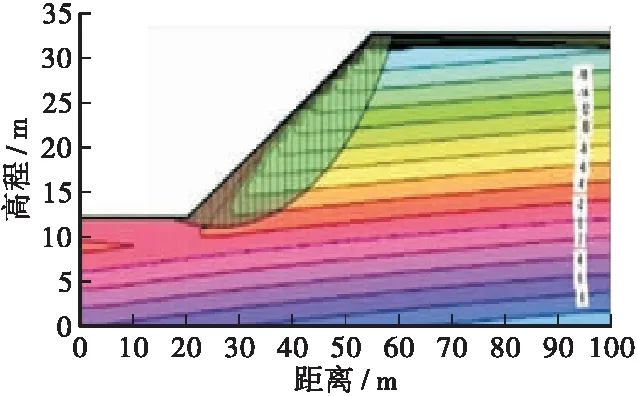
a)T=24 h，FS=1.931

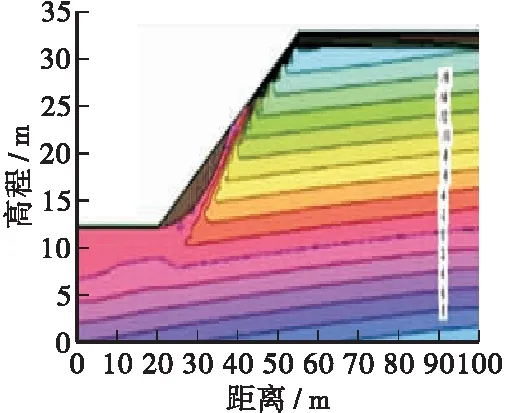
b)T=48 h，FS=1.790

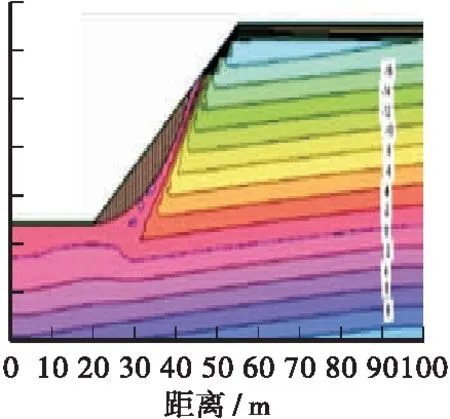
c)T=72 h，FS=1.612

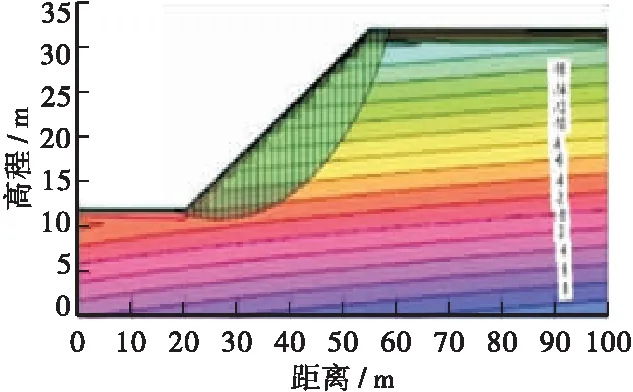
a)T=24 h，FS=1.946

b)T=48 h，FS=1.945

c)T=72 h，FS=1.945

3 结论

通过对不同降雨强度和渗透性情形下的边坡稳定性进行有限元计算分析，得出以下结果：

1)渗透系数越低，边坡就越稳定；边坡的稳定性会随着降雨强度增大而受到不同程度的影响。

2)当降雨强度比边坡的入渗率大时，大部分雨水会形成地表径流而流走，而另较少部分雨水会渗入边坡内部，导致稳定性受到不同程度的影响。

3)渗透系数能决定边坡稳定性影响中降雨强度的极值，故其可作为求取边坡失稳情况下临界雨强的推估条件。

[1] 李媛，孟晖，董颖，等.中国地质灾害类型及其特征-基于全国县市地质灾害调查成果分析[J].中国地质灾害与防治学报，2004，15(2)：29-31.

[2] 中国地质环境信息网.全国地质灾害通报(2006-2013年度)[EB/OL].http://www.cigem.gov.cn.

[3] 石振明，沈丹祎，彭铭，等.考虑多层非饱和土降雨入渗的边坡稳定性分析[J].水利学报，2016,47(8):977-985.

[4] 常金源，包含，伍法权，等.降雨条件下浅层滑坡稳定性探讨[J].岩土力学，2015，36(4)：995-1001.

[5] 蔡瑞卿.降雨诱导的边坡渗流及边坡失稳机理研究[D].成都：西南交通大学，2014.

[6] Geo-Slope internation Ltd.Stability Modeling with SLOPE/W 2007 Version[Z].中仿科技，2007.

[7] 张雪东.土水特征曲线及其在非饱和土力学中应用的基本问题研究[D].北京:北京交通大学,2010.

[8] Genuehten,M.T.A closed form equation for Prediction the hydraulic conductivity of unsaturated soils[J].Soil Science Society of America Journal,1980(44):892-898.