基于灰关联的炭质页岩边坡稳定性影响因素分析

， ，

(长沙理工大学 交通运输工程学院，湖南 长沙 410004)

灰色理论以“部分信息已知，部分信息未知”为研究对象，充分利用已经知道的有用信息，实现对信息演化趋势的正确模拟与预测，它是一种不确定性系统研究方法，由于对观测数据没有特殊的限制，其应用相当广泛。

国内外对炭质页岩边坡的设计中，一般采用经验法、其他岩体类似法等等，并没有定量的分析方法，对其稳定性评价没有科学合理的判别依据，这样会导致设计过于保守、过于依赖类似工程，其风险性较高，施工费用增加，计划工期延长。因此为了能够更好地对此类边坡工程进行分析，就必须把重点放在几个起控制性作用的影响因素上，找到最敏感影响因素对治理失稳、分析失稳破坏原因、模型校正等都有重要研究意义。为此，本文采用坡高、坡角、粘聚力、内摩擦角、岩层倾角和岩土体重度等主要影响因素进行正交试验设计，然后再利用FLAC3D软件进行数值分析，并将数值分析结果稳定系数Fs作为参考序列与各影响因素通过灰关联法进行敏感性分析，找到最敏感影响因素从而为类似工程提供可靠的参考依据。

1 灰色关联分析

对于某个系统而言，通常是由多个确定和不确定因素的共同作用来决定其发展态势，在多种因素中，找到主要及次要因素是十分关键的；在统计学中，常用的分析方法有回归分析、方差分析、主要成分分析，其区别见表1。

表1 3种分析方法劣势回归分析方差分析主要成分分析必须有大量数据样本服从概率分布计算量大

灰色关联分析是对某一个特定的系统发展变化趋势的比较和定量描述的分析方法，是灰色理论中最重要、最基本的方法之一。灰色关联分析对样本数量的多少，样本有无规律都适用，计算量相对小，不会出现定性与定量不符的情况。灰色关联分析的核心是确定参考序列后利用曲线的相似程度来说明多个对象的关系与参考序列比较是否紧密，假如两者曲线非常接近、相似，说明两者之间的关联度很大，即相关性越好，与已知原始数据序列曲线越接近越能够真实反映原始数据序列[1]。

1.1 灰色数据序列无量纲处理

当系统的各相关因素量纲、单位、涵义相同，就无需对数据进行量纲处理，但是，大多数情况下，各相关因素量纲、单位、涵义并不相同，这时需对序列进行无量纲处理，其数据处理方式有4种，如下所示:

设Xi=(xi(1),xi(2),xi(3),…，xi(n))为因素Xi行为序列，xi(k)是第k个值。

1.2 灰色关联系数与灰色关联度

设X0=(x0(1),x0(2),…，x0(n))为系统特征序列，且:

x1=(x1(1),x1(2),…,x1(n))

x2=(x2(1),x2(2),…,x2(n))

…………………………………

xm=(xm(1),xm(2),…,xm(n))

为相关因素序列。

对于ζ∈(0,1)，则灰色关联系数γ0i(k)为：

(1)

将关联性系数取平均值可得到关联度γ(X0,Xi)的计算公式为：

(2)

2 FLAC3D数值模型

FLAC3D软件[2-5]使用体积模量K和剪切模量G进行建模，所做正交试验数量较多，其详情不可能逐一列出，以下对第9组试验的模型进行列出，首先采用Ansys有限元软件进行数值建模，再将数值模型导入到FLAC3D中，建立模型总宽度为30 m，左侧高度为35 m，右侧高度为10 m。模型网格划分共生成928个节点和469个单元，网格划分见图1。

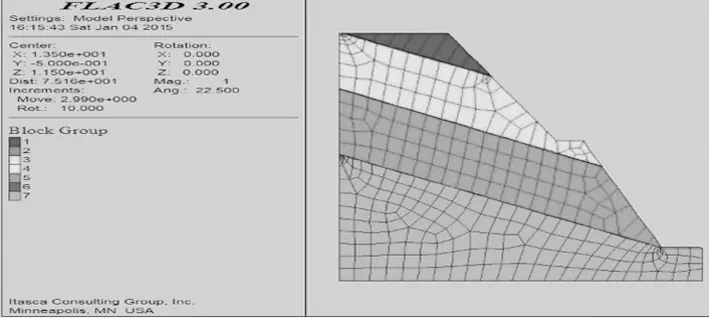
图1 第9组试验网格模型

其余试验模型均可按照上述模型建立方法进行数值模拟计算，鉴于篇幅，部分计算结果如图2～图5所示。

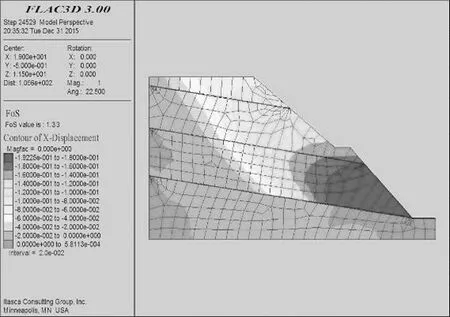
图2 第2组试验稳定系数

图3 第9组试验稳定系数

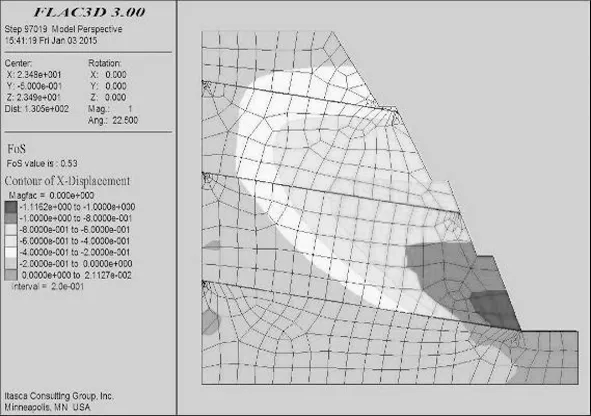
图4 第14组试验稳定系数

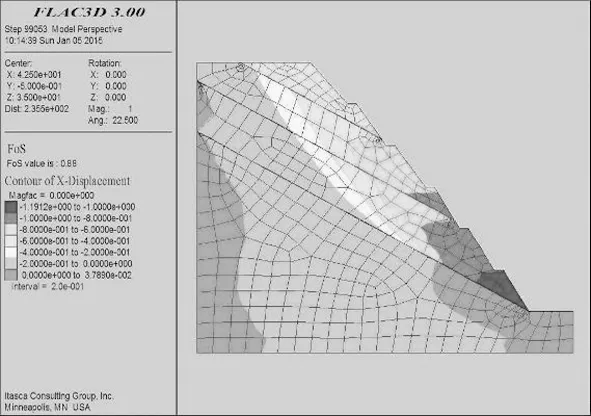
图5 第23组试验稳定系数

3 影响因素敏感性灰关联分析

3.1 炭质页岩边坡正交试验方案设计

对炭质页岩边坡引入正交试验设计的目的是寻求最优水平因素组合，提高研究效率。正交试验的基本思路就是尽量大幅减少试验次数，通过进行少量部分试验与运算，进而推断与分析全面试验的情况。要进行正交试验就必然离不开正交表的指导，该表根据组合数学理论使得试验的组合均匀而全面。进行试验设计时，将各个因素随机填入表列上方，给定各因素水平，选择合适的正交表来确定计算方案，根据这些计算方案进行计算，记录结果，对数据进行分析并得到结论[6-9]。本文正交试验设计采用6因素5水平，只需25次试验，约是全面试验所需次数56=15625的1/625。因素水平表如2所示。

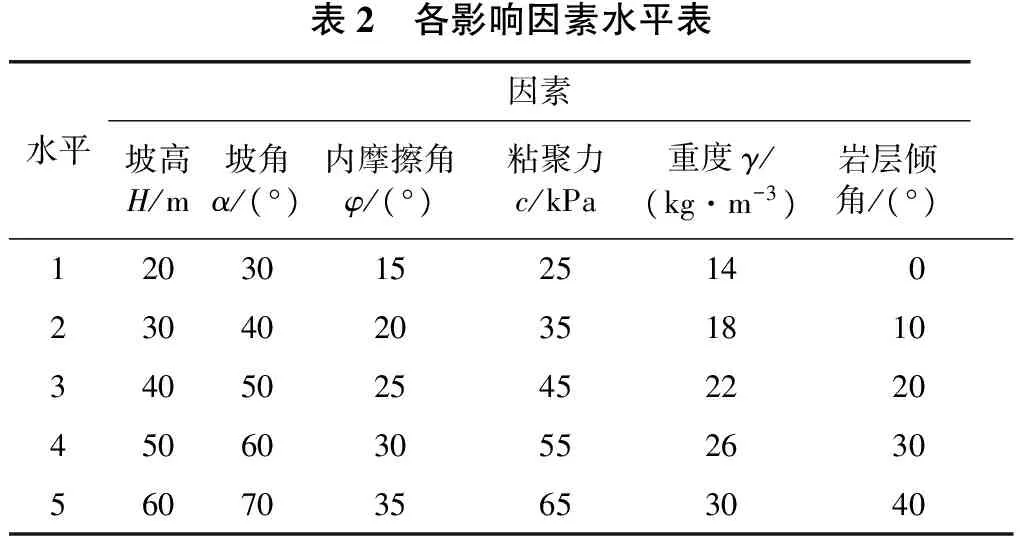
表2 各影响因素水平表水平因素坡高H/m坡角α/(°)内摩擦角φ/(°)粘聚力c/kPa重度γ/(kg·m-3)岩层倾角/(°)12030152514 02304020351810340502545222045060305526305607035653040

根据正交表进行25组建模计算，将得到的结果按照灰色关联分析方法进行灰色关联排序，找到主要影响因素。

3.2 多个影响因素敏感性灰关联分析结果

经过对所有25组不同参数组合的炭质页岩边坡进行稳定系数求解，得到结果汇总如表3所示。

将稳定系数作为参考序列X0，其他6个因素作为比较序列，其中X1为坡高，X2为坡角，X3为内摩擦角，X4为粘聚力，X5为岩石重度，X6为岩层倾角。数据序列的无量纲采用初值化处理，再对各数据序列计算差序列，求得各数据序列计算两级最大差和最小差，再利用关联度公式(2)，计算关联度结果见表4。

由表4灰色关联度计算结果可知，得到影响炭质页岩边坡稳定性的各影响因素敏感性大小关系为：内摩擦角>重度>粘聚力>坡高>坡角>岩层倾角。由此结果可以得出：岩体内摩擦角对炭质页岩边坡稳定性影响最为敏感，反映出岩体抗剪强度的重要性；重度次之，反映出岩体自身的内在属性；粘聚力、坡高、坡角敏感性较小，岩层倾角对边坡稳定性影响最小。因此，根据各个因素的敏感性排序，在同类地区进行炭质页岩边坡设计和分析时有针对性和重点性。

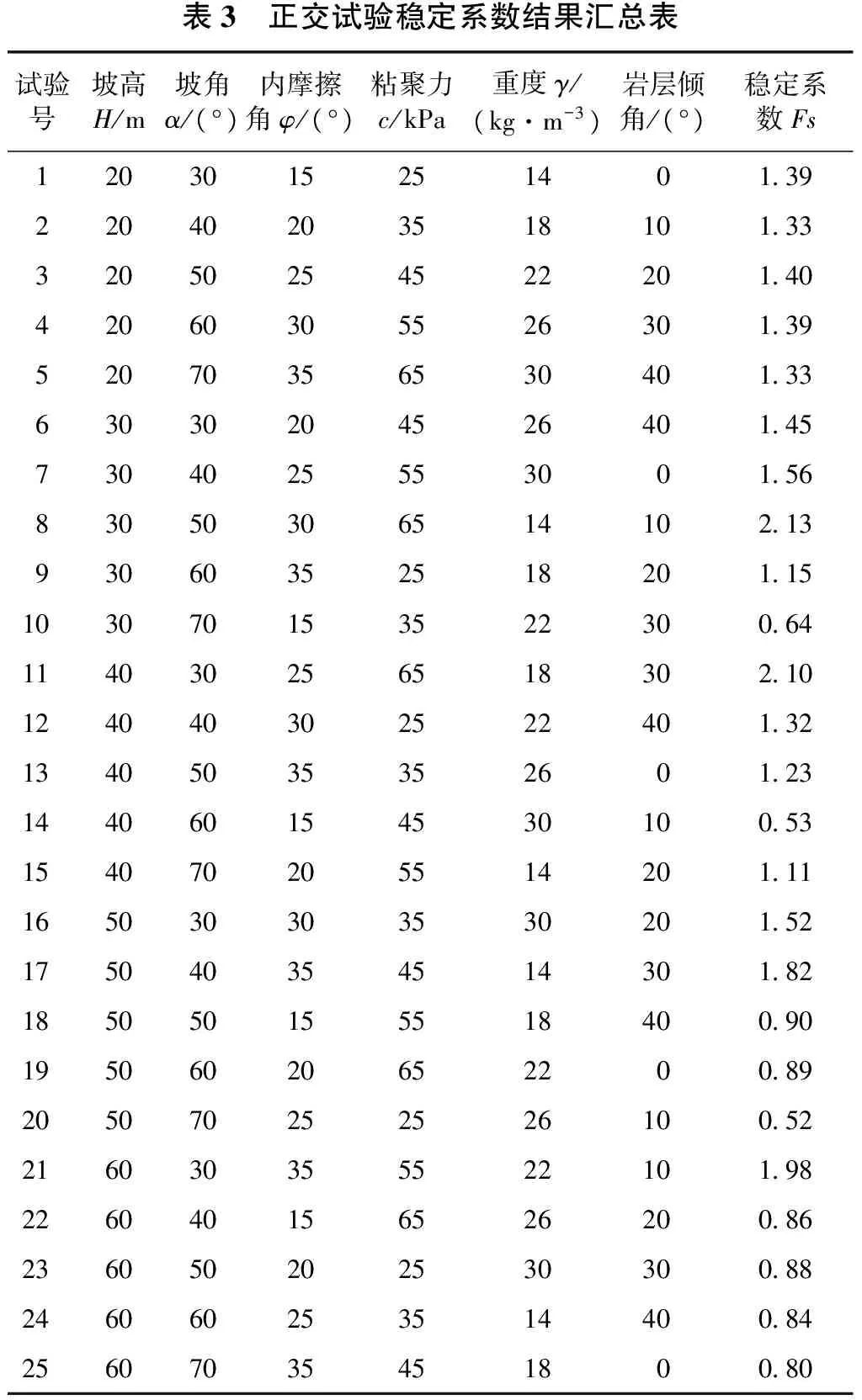
表3 正交试验稳定系数结果汇总表试验号坡高H/m坡角α/(°)内摩擦角φ/(°)粘聚力c/kPa重度γ/(kg·m-3)岩层倾角/(°)稳定系数Fs1203015251401 3922040203518101 3332050254522201 4042060305526301 3952070356530401 3363030204526401 457304025553001 5683050306514102 1393060352518201 15103070153522300 64114030256518302 10124040302522401 3213405035352601 23144060154530100 53154070205514201 11165030303530201 52175040354514301 82185050155518400 9019506020652200 89205070252526100 52216030355522101 98226040156526200 86236050202530300 88246060253514400 8425607035451800 80

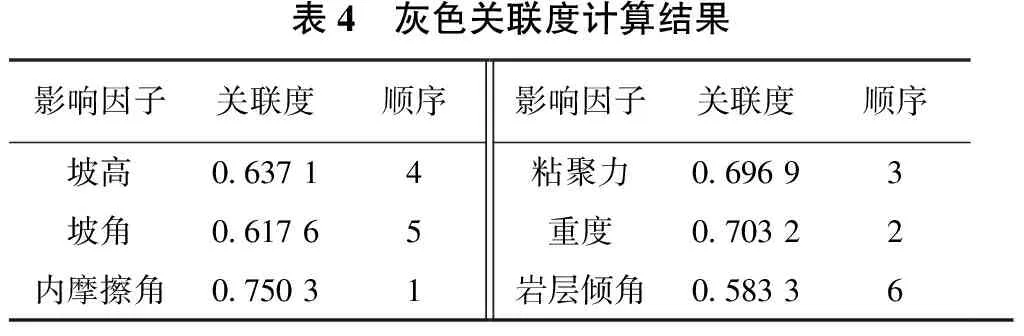
表4 灰色关联度计算结果影响因子关联度顺序影响因子关联度顺序坡高0 63714粘聚力0 69693坡角0 61765重度0 70322内摩擦角0 75031岩层倾角0 58336

3.3 单个影响因素敏感性灰关联分析结果

通过对某一基准模型边坡进行灰关联分析，变化其中一个参数，来考察其影响因素的排序。将炭质页岩岩体参数H=40 m，α=50°，φ=25°，c=45 kPa，γ=22 kN/m3，岩层倾角为20°作为基准值，使各个因素值前后波动引起稳定系数Fs改变，其余参数不变。见表5。

再利用关联度公式(2)，计算结果见表6。

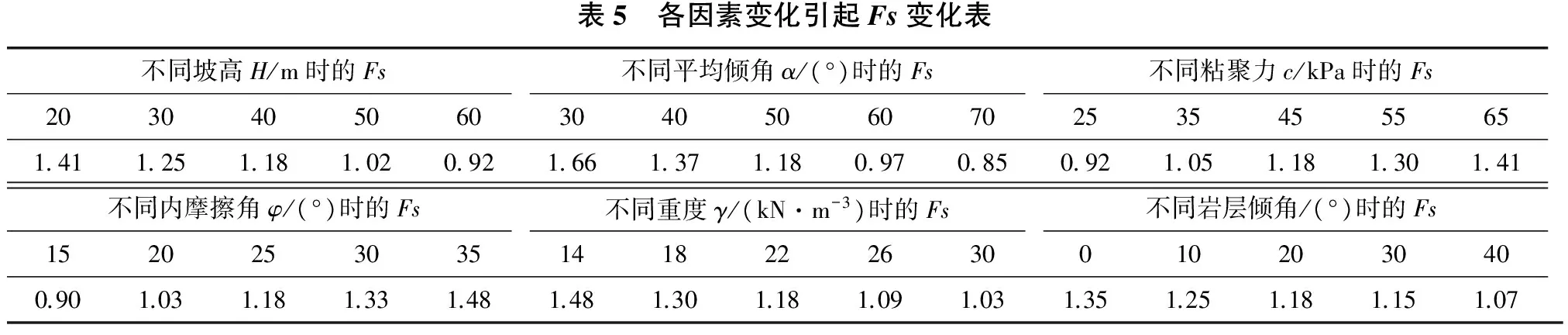
表5 各因素变化引起Fs变化表不同坡高H/m时的Fs不同平均倾角α/(°)时的Fs不同粘聚力c/kPa时的Fs2030405060304050607025354555651 411 251 181 020 921 661 371 180 970 850 921 051 181 301 41不同内摩擦角φ/(°)时的Fs不同重度γ/(kN·m-3)时的Fs不同岩层倾角/(°)时的Fs152025303514182226300102030400．901．031．181．331．481．481．301．181．091．031．351．251．181．151．07

表6 灰色关联度计算结果表影响因子关联度顺序影响因子关联度顺序坡高0．67195内摩擦角0．79801坡角0．55076重度0．70982粘聚力0．68023岩层倾角0．67794

由表6得知，单个影响因素的边坡稳定性灰关联排序为：内摩擦角>重度>粘聚力>岩层倾角>坡高>坡角。与多个影响因素对比发现内摩擦角、重度、粘聚力始终排在前三，两者具有很高的相关性。因此，在对炭质页岩边坡稳定性评价时，敏感因素内摩擦角、粘聚力和重度的取值就显得及其重要，岩体的力学参数应该通过现场试验和室内试验相互结合获得。

对于不同类型的边坡，通常具有不同权重的敏感性影响因素，而决定炭质页岩边坡稳定性因素的前几位因子大致相同，具有某些共性，因此，在实际工程中应具有大局观，做到具体问题具体分析。

4 结论

采用正交试验法进行设计，选用坡高、坡角、粘聚力、内摩擦角、岩层倾角和岩土体重度6个因素，采用6因素5水平进行正交试验，进行了25组的边坡稳定系数求解，按照正交试验的灰色关联分析法对稳定系数计算结果进行了处理，得到多个影响因素敏感性排序为：内摩擦角>重度>粘聚力>坡高>坡角>岩层倾角；得到单个影响因素敏感性排序为：内摩擦角>重度>粘聚力>岩层倾角>坡高>坡角。其中，内摩擦角、重度、粘聚力始终排在前三，两者具有很高的相关性。因此，在对炭质页岩边坡稳定性评价时，敏感因素内摩擦角、粘聚力和重度的取值就显得极其重要，岩体力学参数应通过现场试验和室内试验相互结合获得。

[1] 王丰效.非等距灰色预测模型的应用[J].统计与决策，2006(19)：20-21.

[2] 陈育民，徐鼎平.FLAC/FLAC3D基础与工程实例[M].北京：中国水利水电出版社，2009.

[4] Wang Lei.Application Study of FLAC in Analysis of Slope Stability[A].Proceedings of 2011 International Symposium on Water Resource and Environmental Protection(ISWREP 2011)[C].Xi′an,2011.

[5] Ignacio Pérez,Luis Medina,Miguel Angel del Val.Nonlinear elasto-plastic performance prediction of materials stabilized with bitumen emulsion in rural road pavements[J].Advances in Engineering Software,2016(6):546-564.

[6] 王喜华，赵志明，吴光.正交试验设计的岩质路堑植被边坡稳定参数敏感性分析[J].铁道建筑，2012(10):94-96.

[7] 王飞.考虑c、φ相关性边坡稳定性多因素敏感性分析[J].中国水运，2011(5):227-229.

[8] 陈鹏.公路顺层岩质边坡稳定及其影响因素分析[D].杭州：浙江大学，2012.

[9] 方薇，杨果林，刘晓红.红粘土路堑边坡稳定因素敏感性正交试验分析[J].路基工程，2011(5):59-61.