净距变化时的大偏压隧道施工力学特性研究
(湖南尚上建设开发有限公司,湖南 长沙 410001)
0 引言
随着我国交通基础建设的不断发展,在地形、地貌复杂的西部地区需修建大量长大隧道[1]。由于长大隧道受地形、地质等条件影响较大,为满足路线线性与分离式隧道的净距要求,小净距隧道应运而生并得到广泛应用[2]。因小净距隧道结构型式特殊,在偏压复杂的地形或地质条件下施工难度较大[3]。基于此,笔者运用ABAQUS有限元软件,对大偏压小净距隧道在净距变化时的受力与变形进行数值分析,得出结果可为同类隧道工程的施工提供参考与借鉴。
1 计算模型与工况设计
本文数值模拟计算采用ABAQUS软件建立数值分析模型[4],图1为地层模拟范围,横向距隧道中心的距离均取为45 m,模型两侧边界施加法向约束,模型下边界施加法向与切向约束[5-8]。图2为围岩平面计算模型。
模拟计算过程中隧道仅考虑常规支护,没有对中间岩柱进行加固,拟定净距为 4,6,8,10,12,14,16,18,20 m这9种情况,其中,偏压角度固定为45°,隧道拱肩覆土厚度固定为8 m,围岩参数如表1所示。

图1 围岩平面分析影响范围(单位: m)

图2 围岩平面计算模型
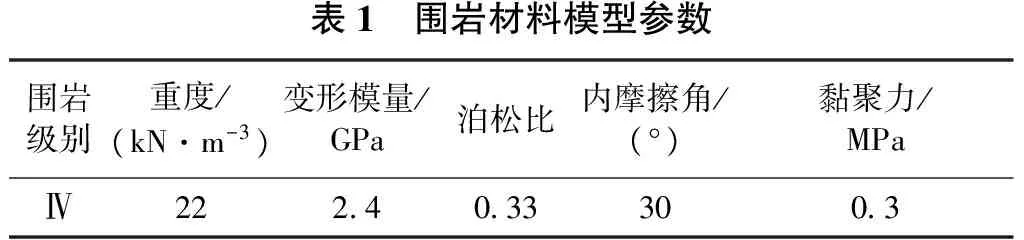
表1 围岩材料模型参数围岩级别重度/(kN·m-3)变形模量/GPa泊松比内摩擦角/(°)黏聚力/MPaⅣ222 40 33300 3
2 围岩塑性区
净距变化时,隧道塑性区形状如图3所示。
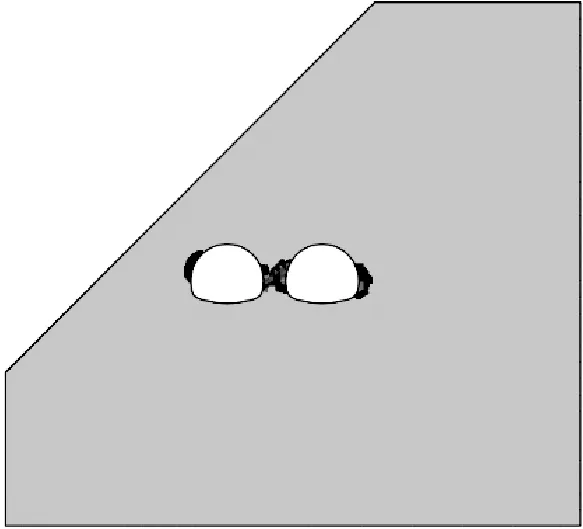
4 m
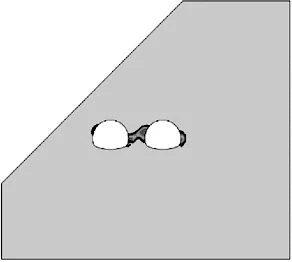
6 m
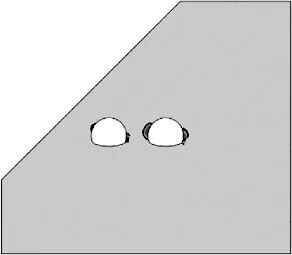
8 m
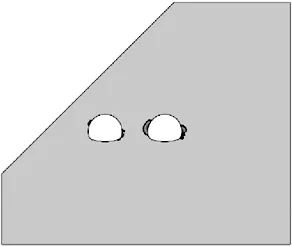
10 m

12 m

14 m
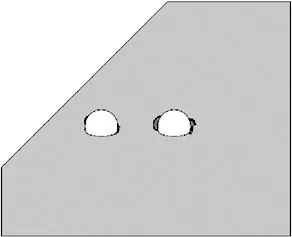
16 m
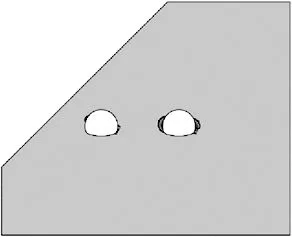
18 m
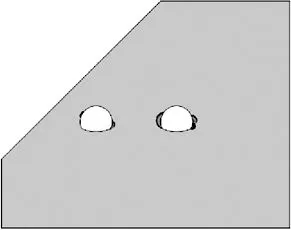
20 m
分析以上各图可知:
1) 当净距为4 m时,中间岩柱的等效塑性区面积较大,且中间岩柱塑性区已出现贯通,塑性区叠加效应显著,可见此时双洞开挖相互影响导致中间岩柱稳定性非常差,最大塑性应变出现在中间岩柱核心区,为18.66×10-3,在净距为6 m时,中间岩柱塑性区呈斜条形分布,呈现出明显的偏压特征,由于偏压作用,深、浅埋洞左右两侧的塑性区分布不对称,浅埋洞的左侧塑性区主要集中在拱肩至拱腰附近,右侧塑性区主要集中在拱脚附近,深埋洞左侧塑性区主要集中在拱腰至拱脚附近,右侧塑性区主要集中在拱脚至墙脚附近。
2) 当净距为8 m时,中间岩柱塑性区从连通到不连通,随着净距的增加,产生塑性变化的区域逐渐减小,围岩稳定性逐渐增加。对于深、浅埋洞左右两侧的塑性应变区域,当净距d≥8 m,浅埋洞的塑性区域基本不再变化,与净距4~6 m时的分布位置一样,而深埋洞的塑性区域随着净距的增大,逐渐由以前的左右分布不对称形式变成对称分布的形式,在净距d=18 m时,两侧塑性区分布基本对称,表现出单洞隧道深埋无偏压的特点。如果把塑性区是否连通作为选择小净距隧道最小合理净距的原则,那么按照此方法计算出来的最小合理净距应该是8 m左右。
3) 从表2、图4可知,当净距d在8 m左右的时候,中间岩柱中最大塑性应变有突变,当净距小于8 m时,塑性应变大小迅速增大,表明隧道处于不稳定状态;当净距大于8 m时,塑性应变大小基本不再变化。从最大塑性应变角度来分析,当净距d=8 m左右时发生突变,因此其最小合理净距应为8 m左右。
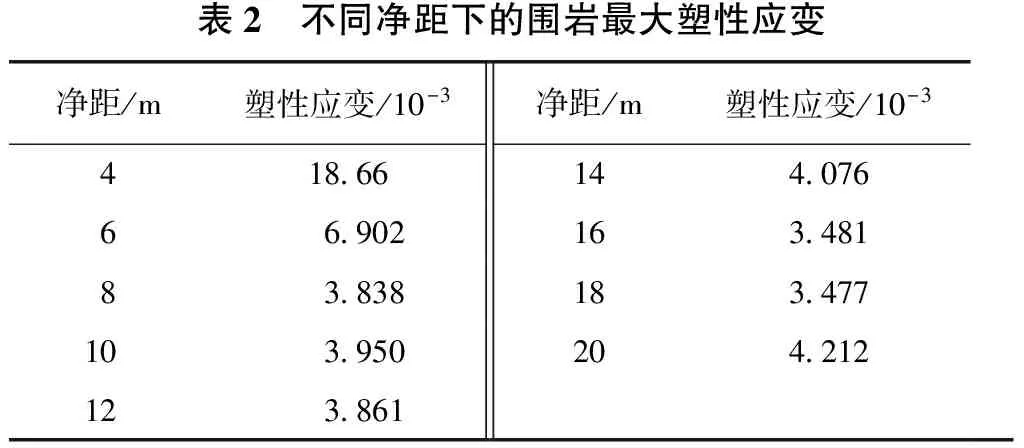
表2 不同净距下的围岩最大塑性应变净距/m塑性应变/10-3净距/m塑性应变/10-3418 66144 07666 902163 48183 838183 477103 950204 212123 861
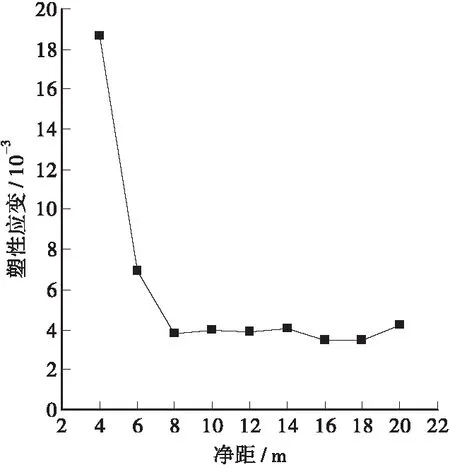
图4 围岩塑性应变图
3 围岩应力分析
围岩应力分析选取的分析点如图5。
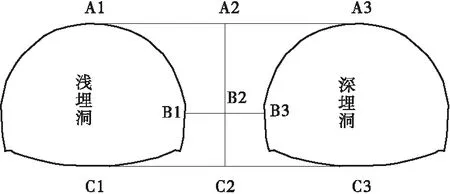
图5 中间岩柱特征点布置图
运用岩石抗剪安全系数Kα计算各特征点的抗剪安全系数:
式中:Kα为抗剪安全系数;φ为摩擦角;c为粘聚力;σ1、σ3分别为最大、最小主应力。
图6、图7分别为最小、最大主应力图。

图6 最小主应力图
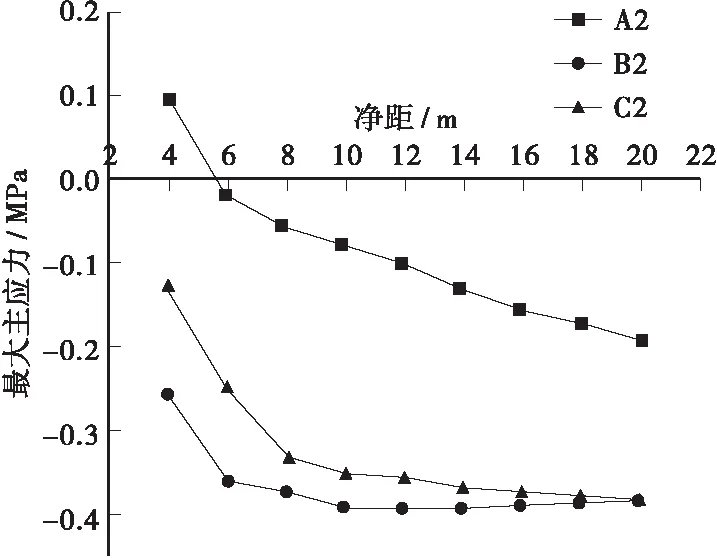
图7 最大主应力图
1) 由图6、图7可知,随着净距的增大,中夹岩体核心区的最小主应力的绝对值逐渐减小并最终趋于稳定,变化最大的特征点为B2,最大主应力的绝对值逐渐增大并最终趋于稳定,变化最大的特征点为A2,最大与最小主应力之间的差值越来越小,表明特征点的稳定性越来越好。
2) 对于最小主应力,以特征点B2的变化来说明,第1阶段,净距在4~8 m之间,随净距的增大,最小主应力绝对值开始迅速减小,双洞开挖叠加效应明显;第2阶段,净距在8~12 m之间,随净距的增大,最小主应力绝对值减小速度减慢;第3阶段,即当净距大于12 m时,随着净距的增大最小主应力变化不大,推测此时双洞隧道呈相互独立、互不干扰趋势;最大主应力的变化跟最小主应力一样,此处不再赘述。
3) 从图8围岩抗剪安全系数随净距变化的曲线可知,各特征点的变化规律基本一致,但存在数值上的差别,各特征点的安全系数随着净距的增大逐渐增大,且增大速度越来越小,最终将趋于稳定。以围岩抗剪安全系数允许值[K]≥1.2为判别条件,达到这一条件,A2、B2、C2所对应的净距分别为13.1、8.4、6.8 m,中间岩柱的上部抗剪安全性小于下部。随着净距的增大,围岩抗剪安全系数变化最大的点为B2,且该点最终的安全系数也最大,说明净距越大,中间岩柱中心处越稳定,抗剪安全系数最先达到稳定的特征点为C2,最后达到稳定的特征点为A2。在净距为4~6 m的时候,各特征点抗剪安全系数基本保持不变,且均小于安全系数允许值,说明在净距过小时,如不采取适当的加固措施,中间岩柱极有可能已发生剪切破坏。
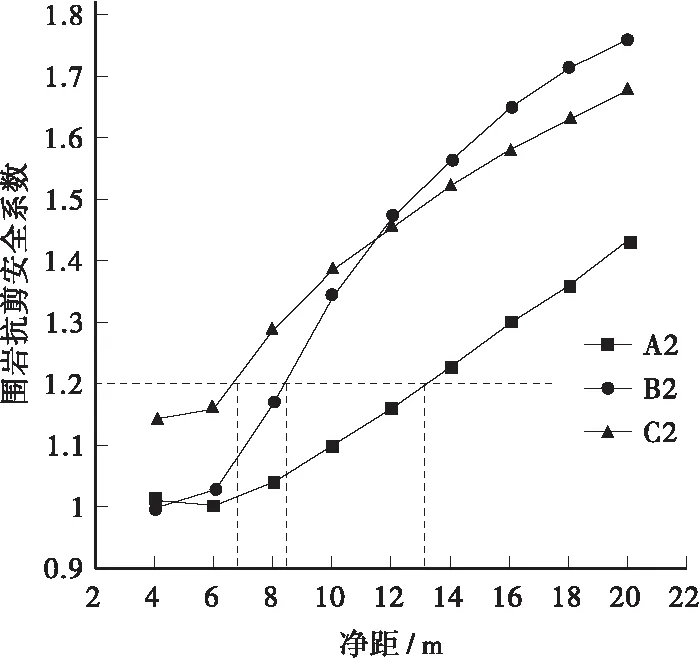
图8 特征点围岩抗剪安全系数变化曲线
4 围岩位移分析
布置如图9所示监测点。
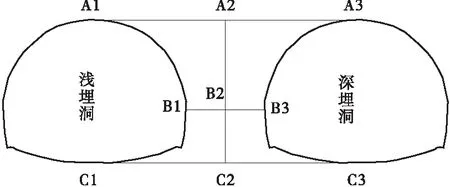
图9 中间岩柱监测点布置图
通过数值计算得到各监测点位移随净距的变化如图10所示。
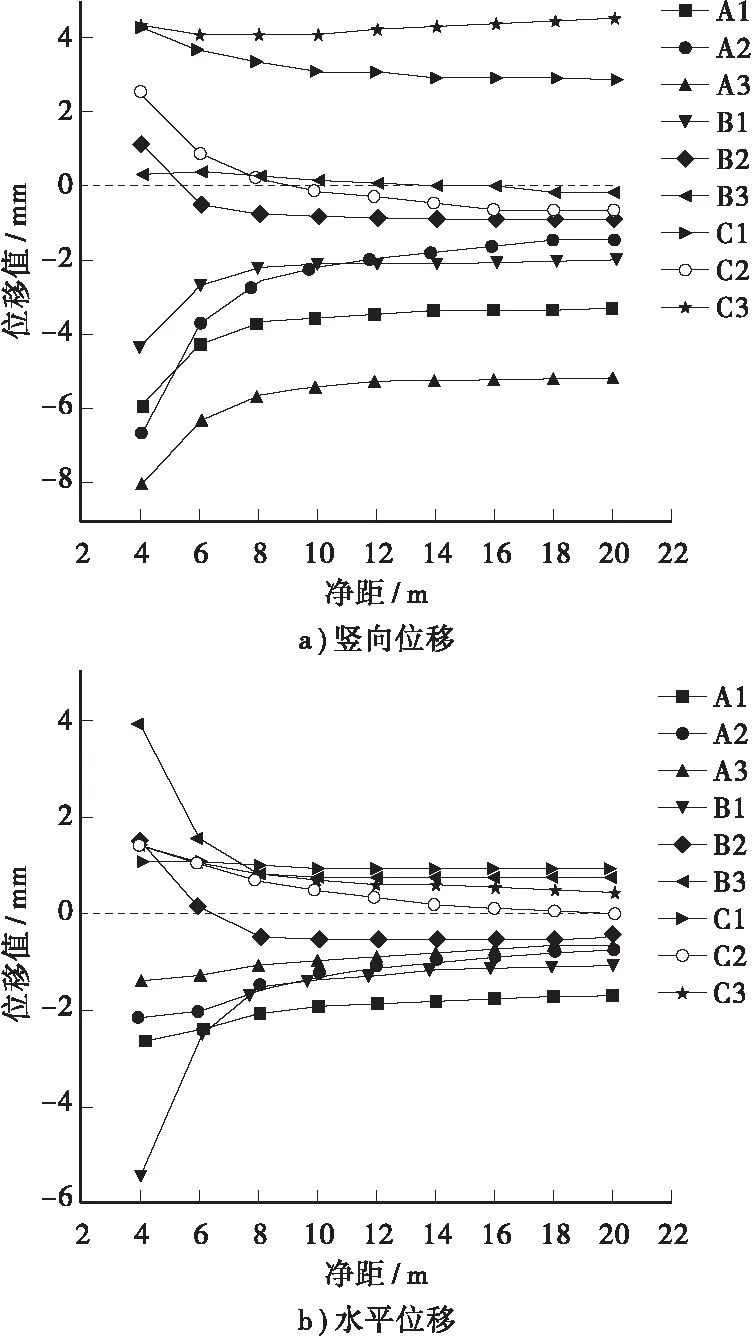
图10 中间岩柱特征点位移变化曲线
由图可知:
1) 中间岩柱各监测点竖向位移呈自下而上逐渐增大的分布规律,同时由于深埋侧埋深较大,使得中间岩柱深埋侧特征点竖向位移大于浅埋侧。
2) 各特征点竖向位移随着净距的增大呈非线性的递减变化,除了中间岩柱下部的C1、C2、C3以及B3竖向位移为正(即隆起)之外,其余各点竖向位移均为负(即沉降),竖向位移受净距影响较小的点为B3和C3,均在中间岩柱深埋侧,位移曲线保持为一条近似的水平线,其余各点的竖向位移受净距的影响较大,变化基本分为以下几个阶段:第1阶段,净距在4~8 m之间,随净距的增大,特征点竖向位移开始迅速减小,双洞开挖叠加效应明显;第2阶段,净距在8~12 m之间,随净距的增大,特征点竖向位移减小速度减慢;第3阶段,即当净距大于12 m时,特征点竖向位移变化不大,近似一条水平直线,推测此时双洞隧道呈相互独立、互不干扰趋势,这与前面围岩应力和支护结构内力的变化规律基本一致。
3) 当净距较小时,中间岩柱水平位移最大的点为B1和B3,且两者水平位移方向刚好相反,该区域在围岩塑性区分布图中正为中间塑性区贯通区域,当净距较大时,中间岩柱水平位移最大的点为A1和C1,方向也相反。
5 支护结构内力分析
将衬砌轮廓按角度分割,如图11所示。

图11 衬砌轮廓分割图
衬砌结构不同角度处轴力分布如图12。

图12 不同净距下衬砌轴力分布图
1) 从图12衬砌结构轴力分布的变化规律可知,在隧道净距从4 m增至8 m过程中,靠近中间岩柱侧衬砌结构轴力值变化幅度较大且减小,当净距大于8 m之后,随着净距的增加,衬砌结构轴力基本不再发生变化,分析原因是因为随着两洞净距增大,应力重分布区域有所减小或者叠加影响较小,导致衬砌轴力值减小;同时从上图也可以看出,不同净距下衬砌轴力沿隧道轮廓的分布形状基本不发生改变,说明净距对于隧道偏压的影响不大。
2) 从图13隧道各控制点衬砌轴力变化曲线可知,对于浅埋洞,衬砌结构下部轴力大于上部,拱底和拱顶处的轴力较小,各控制点轴力随着净距的增加均逐渐减小,当净距在4~8 m范围内时,轴力变化较快,双洞开挖叠加效应明显,当净距在8~12 m范围内时,轴力变化减慢,当净距大于12 m时,轴力基本保持不变。对于深埋洞,衬砌结构中部轴力大于上部和下部,同样也是拱底和拱顶处的轴力较小,随着净距的增加,拱顶、外拱肩以及外墙脚的轴力逐渐增加,其余特征点轴力逐渐减小,当净距大于10~12 m后,轴力基本保持不变,与浅埋洞变化规律基本一致。
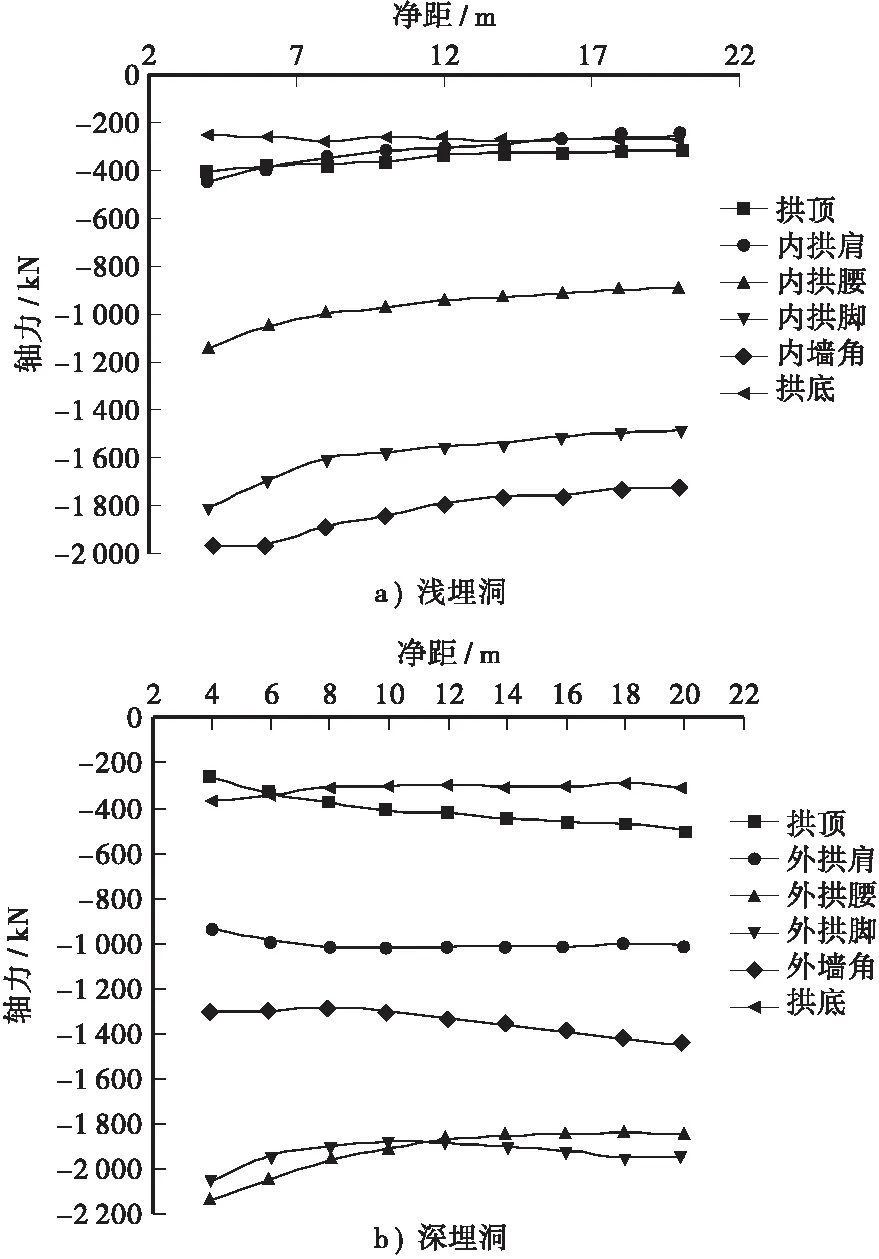
图13 隧道各控制点衬砌轴力变化曲线
6 结论
1) 净距的变化对中间岩柱的影响最为显著,对隧道偏压效应的影响不大。
2) 随着隧道净距的变化,靠近中间岩柱侧衬砌结构轴力值调整幅度大于远离中间岩柱侧,且靠近中间岩柱处衬砌各控制点轴力随着净距的增加逐渐减小。
3) 围岩、中间岩柱及支护结构的各项指标随净距的变化大致经历了3个不同的阶段,第1阶段为双洞叠加效应明显阶段(4~8 m,净距约小于0.6B,B为洞跨,下同),该阶段双洞叠加效应明显,各项指标受净距变化的影响较大;第2阶段为双洞叠加效应减弱阶段(8~12 m,约为0.6B~1B),该阶段双洞叠加效应减弱,各项指标随净距的改变会有变化,但变化趋势减弱;第3阶段为双洞相互独立阶段(大于12 m,约为1B),该阶段双洞隧道呈相互独立、互不干扰趋势,各项指标不再随净距改变而发生明显的变化。
4) 从围岩、中间岩柱及支护结构的受力和变形特性随隧道净距的变化情况来看,在具体地形及地质条件限制地段,陡坡偏压隧道最小安全净距以不小于8 m(0.6B)为宜,可以使得双洞相互影响适中,且深埋洞埋置深度不至于过大,在具体地形及地质条件不受限制地段,陡坡偏压隧道最小安全净距以不小于12 m(1B)为宜。
[1] 李积栋,陶连金,油新华,等.不同净距垂直交叉组合地铁车站结构地震响应研究[J].岩石力学与工程学报,2016(S2):3890-3897.
[2] 王帅帅,高波,全晓娟,等.不同地质条件下浅埋偏压小净距隧道围岩稳定性研究[J].水文地质工程地质,2014(3):60-65.
[3] 赵斌,敖芃,李文涛.不同埋深下小净距隧道最优净距的探讨[J].铁道建筑,2013(8):68-71.
[4] 赵孝辉,徐国元.小净距隧道中间岩柱在不同净距下的受力分析[J].公路,2011(7):270-273.
[5] 赵孝辉,徐国元.小净距隧道中间岩柱在不同净距下的受力分析[J].中外公路,2011(3):233-236.
[6] 陈志荣,王刚,沈习文.小净距隧道在不同净距及偏压条件的数值模拟[J].路基工程,2008(2):115-117.
[7] 姚勇,晏启祥,周俐俐.小净距隧道在不同开挖方式下的力学效应分析[J].西南科技大学学报(自然科学版),2005(2):53-56,74.

