边坡工程中土拱厚度的计算方法研究

，

(江苏科技大学 土木工程与建筑学院，江苏 镇江 212003)

0 引言

在抗滑桩加固土坡的过程中，随着土体位移的增长,桩间土体经常会产生“拱”状受力体，称之为“土拱效应”。这种现象是因为介质的不均匀位移产生的。拱后或拱上的压力被它传递到了拱脚及四周的稳固介质中，使介质中的应力形式发生了改变，引起了应力的重新分布。也就是说，土拱通过土体抗剪强度的发挥作为载体来描绘应力转移现象[1-5]。

由于桩与桩之间的相互挤压作用而形成土拱，土拱分为大拱和小拱，大拱和小拱的厚度差即为拱厚。研究表明，土体在成拱的情况下，拱高和拱厚主要受桩间距和桩的截面尺寸的影响，甚至是摩擦角ψ和粘滞力C对其影响基本上都可以不用考虑。而文献[6]相关的实验数据表明截面尺寸对拱厚的影响很小基本上可以忽略不计。而传统的计算拱厚公式均考虑了截面尺寸的作用，这样势必会和实际拱厚有较大的误差，为了提高计算拱厚的准确性，本文对文献[7]拱厚的相关计算公式进行了改进，以期待对实际工程领域起到一定的促进作用。

1 拱厚的主要影响因素分析

土体受力后因产生不均匀位移使土颗粒之间发生相互的 “楔紧”作用而产生了土拱效应。一般认为，土颗粒的传力路径和土体的不均匀位移主要与桩的截面尺寸和桩间距有关[6]。研究表明:土体在成拱的情况下，拱高和拱厚主要受桩间距和桩的截面尺寸的影响，而其它的相关因素，甚至是摩擦角ψ和粘滞力C对其影响基本上都可以不用考虑。本文只考虑桩间距和桩的截面尺寸两个因素对拱高和拱厚所产生的影响。

一般认为，土拱的高度主要由抗滑桩的截面尺寸和桩间距决定。本文用圆桩作为实例运用以下2种方式探讨该因素与土拱尺寸之间的相关关系。

首先在保持圆桩半径不变而改变桩间距的情况下，得出土拱(大、小拱)高度随桩间距的变化情况如表1。从实验数据可以看出随着桩间距的增加，小拱的拱高有减小的趋势且变化较小，大拱的拱高相对来说增速很快，拱厚的变化比较明显，表明桩间距对土拱的高度和土拱的厚度影响很大(其主要是通过改变土拱在拱脚处与x轴的夹角θ而改变拱厚)。

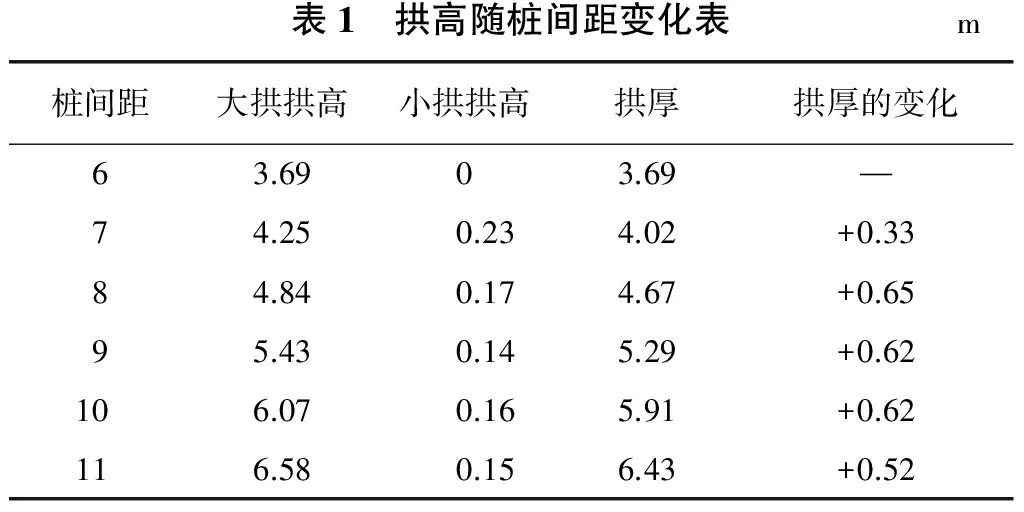
表1 拱高随桩间距变化表m桩间距大拱拱高小拱拱高拱厚拱厚的变化63．6903．69—74．250．234．02+0．3384．840．174．67+0．6595．430．145．29+0．62106．070．165．91+0．62116．580．156．43+0．52

在圆桩间距保持不变的情况下：在一定的范围内改变圆桩的直径，其相关的变化情况如表2。随着圆桩直径的增大,小拱的拱高只有在桩径增大到一定程度后才会有较小的变化，而大拱的拱高虽随着桩径的增大在变化，但变化很小。

从实验数据可以看出：随着桩截面尺寸的增大，大、小拱拱高变化均很小，拱厚有略微几厘米的变化，可能是由于桩与土体之间的挤压造成的，基本上可以忽略桩径对拱厚的影响。

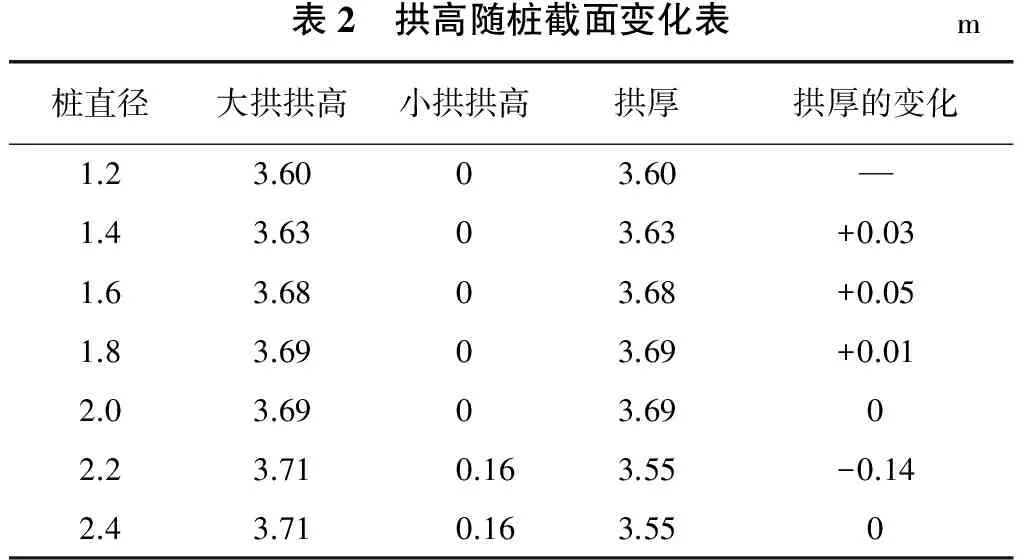
表2 拱高随桩截面变化表m桩直径大拱拱高小拱拱高拱厚拱厚的变化1．23．6003．601．43．6303．63+0．031．63．6803．68+0．051．83．6903．69+0．012．03．6903．6902．23．710．163．55-0．142．43．710．163．550

总之上述结论进一步地说明，在土体可以成拱的前提下：桩径d一定时桩间距对拱厚会产生较大的影响(其主要是通过改变土拱在拱脚处与x轴的夹角θ而改变拱厚)；但在桩间距一定时，桩径对拱厚的影响很小，绝大部分在5 cm的范围内(可能是由于桩与土体之间的挤压造成的)基本上可以忽略不计。

而现有的文献[7]计算拱厚的公式考虑到了桩径，这样会使得求算出来的拱厚比实际的大，为了使求算出来的拱厚更加接近实际，本文对拱厚t的求算公式进行如下完善和改进。

2 对拱圈厚度t计算方法的完善和改进

本文上节的表1和表2的实验数据主要引用于：文献[6] 《土拱效应的尺寸研究》中的相关实验数据，并对其进行了总结分析和深化。

目前现有的拱厚t的求解公式[7]如图1所示。

设桩两边长度为d、b，土拱厚度设为t，土拱在拱脚处与x轴的夹角设为θ。则土拱厚度可近似用下式表示：

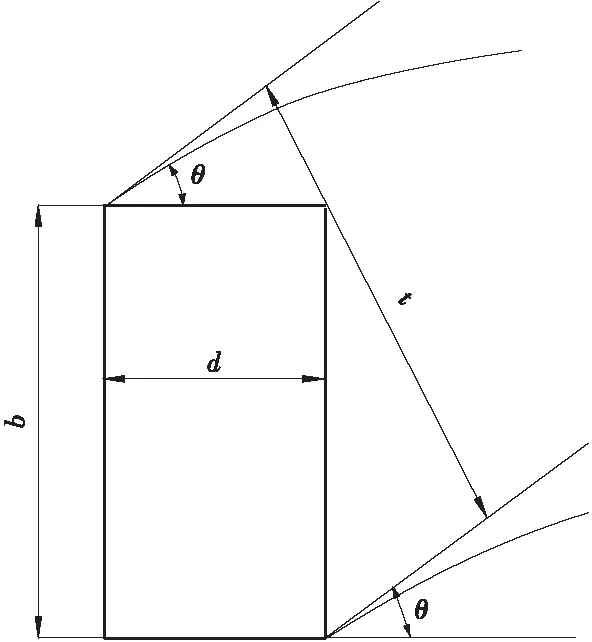
图1 桩间土拱厚度示意图

t=dsinθ+bcosθ

(1)

为了安全起见，对上述土拱厚度根据实际情况乘以一定的折减系数进行使用，则：

t=ξ(dsinθ+bcosθ)

(2)

以上公式考虑了桩的截面尺寸对拱厚的影响，而本文上节实验数据表明：在边坡工程中(边坡工程中桩径d一般不大于3 m)，桩的截面尺寸在一定的程度上对拱厚t影响很小，相对于桩间距对拱厚的影响而言基本上可以忽略不计，这种情况下如果仍考虑桩的截面尺寸求算拱厚，会与实际存在的拱厚产生较大的误差。

综合本文上节实验数据所得结论，为了更为准确地求算拱厚t，在实际工程中应按以下公式对拱厚t进行求解：

对土拱拱圈厚度的分析如图2所示：以圆桩为例，设桩两边长度为d、b，土拱厚度设为t，土拱在拱脚处与x轴的夹角设为θ(θ随着桩间距S的变化而变化)。

图2 桩间土拱厚度示意图

此时土拱厚度可近似用下式表示：

t=bcosθ

(3)

为了安全起见，对上述土拱厚度根据实际情况

乘以一定的折减系数进行使用，则：

t=ηbcosθ

(4)

3 实例分析

为了论证本文提出公式的准确性，本文特别对拱厚做了个试验进行实测测定拱厚。本试验中实例，取其中一组数据d=1.2 m，θ=30°，b=2.1 m，需要确定拱厚t。

如果采用文献[7]中提及拱厚t计算公式进行求解，将相关参数代入式(1)，计算拱厚t=2.42 m(不考虑安全系数的折减)。

若采用本文改进后的拱厚t计算公式，将相关参数代入到式(3)，计算拱厚t=1.82 m(不考虑安全系数的折减)。

而在试验操作中，实测拱厚t=1.64 m，表明经改进后的拱厚t的计算公式比较符合工程实际。因而，如果按照文献[7]中提出的拱厚t的计算公式，由于考虑了桩径的影响，使得其值偏大。而采用本文的拱厚t的计算公式，在考虑适当的折减系数的情况下，其值比较接近实际值。所以，通过与实验实际数据的对比分析，笔者提出的拱厚t的求解公式具有更好的工程实用性。

4 结语

本文基于边坡工程中的土拱理论，探讨了土拱的发展历史，通过对拱厚的主要影响因素分析的基础上对拱圈厚度t的计算方法进行了完善和改进，得出了如下结论：

1) 在能够形成土拱的前提下保持桩半径不变情况下，桩间距对土拱的高度和土拱厚度的影响很大。

2) 在能够形成土拱的前提下桩间距一定时，桩径对拱厚的影响很小，基本上可以忽略不计。

3) 对文献[7]中的求拱厚t的公式进行完善和改进，使求解得到的结果更加接近实际值，从而为实际工程提供了更为可靠的计算依据。

[1] 周德培，肖世国，夏雄.边坡工程中抗滑桩合理桩间距的探讨[J].岩土工程学报，2004,26(1);132-135.

[2] 朱碧堂，刘一亮.基坑开挖和支护中的土拱效应[J].岩土工程师，2001,13 (1).

[3] 周小文，淮家骆，包乘纲.砂土中隧洞开挖稳定机理及松动土压力研究〔J].长江科学院院报，1999,16(4):9-14.

[4] 贾海莉，王成华，李江洪.关于土拱效应的几个问题[J].西南交通大学学报，2003,38(4):398-402.

[5] 吴能森，郑建荣.人工挖孔围护桩受力机理的研究与探讨[J].岩土工程技术，1997,16(3):26-30.

[6] 琚晓冬，冯文娟.土拱效应的尺寸研究[J].灾害与防治工程，2005(2).

[7] 龚志芳.抗滑桩间土拱效应及其数值模拟研究[D].贵阳：贵州大学,2015.

[8] 杨磊.容乌高速公路边坡稳定性分析与安全防护分析[J].公路工程，2017，42(1)：123-126.