藏东南地区高陡边坡稳定性数值分析

,,,

(西藏农牧学院,西藏 林芝 860000)

0 前言

西藏地处我国西南边疆，是我国的生态安全屏障。藏东南地区位于青藏高原东南部，东南较低，西北较高。该地区处于雅鲁藏布江构造带以南地区及东部昌都弧形构造带附近，地震活动频繁，岩体破碎，边坡容易发生失稳[1]。藏东南地区由于受印度洋暖湿季风的影响，雨季旱季分明。雨季为4月至10月，旱季为11月至3月[2]。在雨季期印度洋季风自西向东，水汽经雅鲁藏布江下切峡谷，源源不断地进入藏东南地区。水汽在上升过程中，形成降水。降雨入渗，导致边坡土体抗剪强度降低，加大了边坡失稳的概率。通过现场调研、室内试验，初步掌握了边坡失稳的成因和土体强度特性。同时基于ABAQUS强度折减法对边坡进行稳定性分析，探索边坡失稳的安全系数变化规律，指导边坡失稳防治措施的施工和工程建设的选址，尽量避开容易失稳的边坡，进行工程项目的建设。

1 现场调研

本次试验选取了林芝市巴宜区S306旁一处滑坡体进行现场研究。该滑坡体地处东经94°22′01″，北纬29°35′37″。通过指南针地图手机软件，导出该处滑坡体卫星地图，如图1所示。

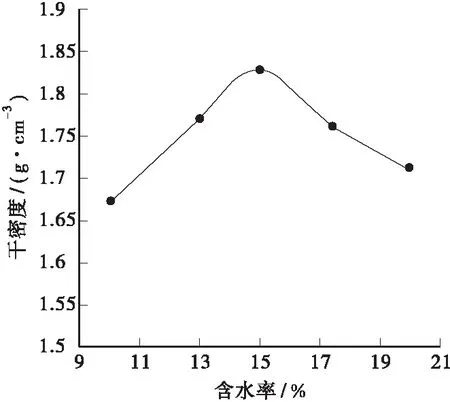
图1 滑坡体地形图

从图1可以看出，该处边坡上部存在漏斗状的地形，雨水容易汇集，土体含水率增加，使得土体抗剪强度降低。导致该处边坡滑坡的产生。

2 室内试验

2.1 击实试验

将取回的滑坡体土样风干，并测得其风干含水率。试验土样最大粒径小于20 mm，可采用重型击实试验，其单位体积击实功为2684.9 kJ/m3。

按下式计算其加水量：

(1)

式中：mω为土样所需加水质量，g；m为风干含水率土样质量，g；ω0为风干含水率，%；ω为配制土样的含水率，%。

分别将配制含水率为10%，13%，15%，17.5%和20%的土样，闷料24 h后进行重型击实试验。分5层击实，每层土质量为900～1100 g，每层击56下，两层间接触土用刮土刀刮毛，以保证土体击实后形成整体。击实完成后，用推土器从击实桶内推出土样。

按下式计算各试样的含水率：

(2)

式中：ω为含水率，%；m为湿土质量，g；md为干土质量，g。

则各试样的干密度为：

(3)

式中：ω为含水率，%；ρ为湿密度，g/cm3；ρd为干密度，g/cm3。

干密度与含水率的关系曲线如图2所示。

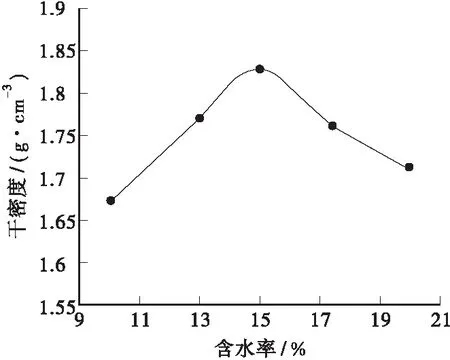
图2 击实曲线

从图2可知，干密度随含水率先增后减，在含水率为15%附近出现峰值，最大干密度为1.83 g/cm3。在含水率为15%附近土体的抗剪强度最大，为剪切试验含水率的配制提供了参考。

2.2 剪切试验

本次试验采用ZJ型应变控制式直剪仪。试验前将风干土样，过2 mm的筛。分别对土样施加100、200、300和400 kN的竖向荷载。试样面积为30 cm2，高为2 cm。测量土样破坏时的测力计读数。按下式计算试样的剪应力：

τ=CR

(4)

式中：τ为剪应力，kPa；C为量力环校正系数，kPa/(0.01 mm)；R为量力环中测力计读数，0.01 mm。

试验成果整理见图3。

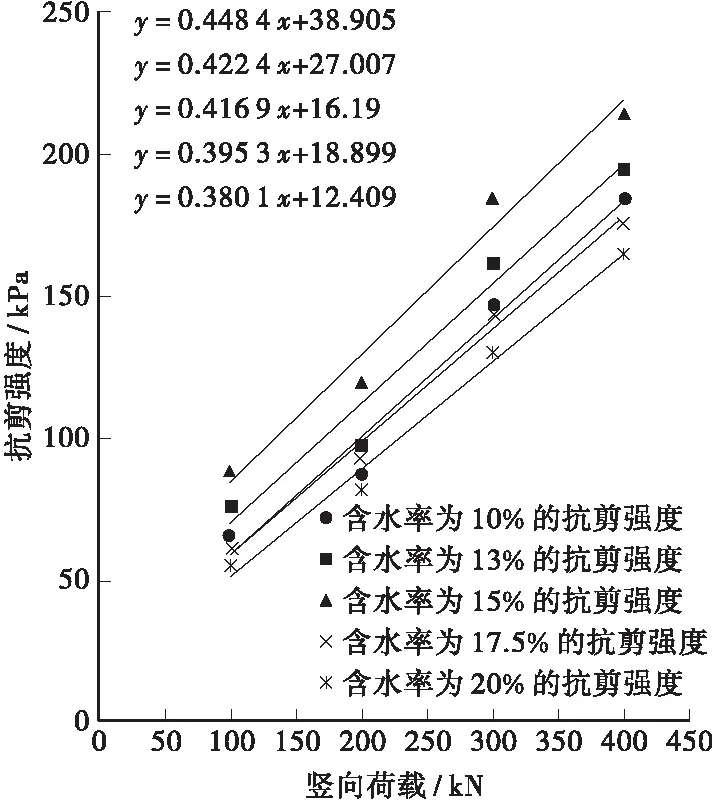
图3 不同含水率下试样的抗剪强度

从图3所示的抗剪强度可看出，含水率为15%时，试验土样的黏聚力c为38.905 kPa，内摩擦角φ为24.15°，抗剪强度为最大值。验证了接近最优含水率时的土样抗剪强度最大。含水率小于15%时，随着含水率的增加，黏聚力c和内摩擦角φ都随之增加。土样含水率低于15%时，抗剪强度随着含水率的增加是因为进行重塑土的抗剪试验时改变了土体结构，接近最优含水率击实效果最好，因而抗剪强度最高。并不能说明含水率增加提高了抗剪强度[3]。含水率大于15%时，随着含水率的增加，黏聚力c和内摩擦角φ随之减少。黏聚力c随含水率的变化较明显，含水率对内摩擦角φ的影响不大。而且其降低幅度较界限含水率之前的增加幅度较大。其原因是含水率增加导致基质吸力减小，黏聚力c随基质吸力的减小而减小。内摩擦角φ的减小是因为含水率的增加导致摩擦系数减小，但含水率对内摩擦角φ的影响相对较小。藏东南雨季降雨频繁，雨量充沛，边坡中的水由于地形和坡度等原因不能及时排出，很容易导致边坡含水率超过15%。边坡土体含水率超过15%后黏聚力c和内摩擦角φ显著下降。土体抗剪强度降低后边坡就很容易发生失稳。

3 有限元强度折减法

3.1 强度折减理论

1975年Zienkiwicz[4]等最早将强度折减理论提出并应用于土坡稳定性分析，强度折减理论应用于边坡稳定性分析得到了广泛的认可。

传统的土坡稳定性方法是极限平衡法。这种方法将土体看作刚塑性体，假定了滑动面的形状和位置，不能考虑实际的应力应变关系。相对于传统边坡稳定性分析方法，强度折减法不需要对滑动面的位置和形状进行假设，考虑土体为弹塑性体的抗剪强度参数和材料属性，能够反映边坡塑性区域是如何从局部发展到整体的。强度折减法将土体的抗剪强度除以安全系数进行折减后得出黏聚力和内摩擦角的计算公式如下式所示：

(5)

(6)

式中：c、φ为土体所能够提供的抗剪强度；cm、φm为维持平衡所需要的或土体实际发挥的抗剪强度；Fr为强度折减系数。

3.2 有限元强度折减法边坡失稳的判断标准

目前相关文献对强度折减法有3种判断标准[5],现归纳如下:

1) 有限元迭代过程不收敛作为边坡失稳的判断标准；

2) 有限元计算模型出现贯通的塑形区域作为边坡失稳的判断标准；

3) 有限元模型特征部位位移发生突变作为边坡失稳的判断标准。

3.3 本构模型的选取

强度折减法选取土体为弹塑性模型，认为土体发生弹性变形和塑性变形。弹性变形采用胡克定律表示，塑性变形一般选取Mohr-Coulomb模型[6]。屈服面的函数表示如下式所示：

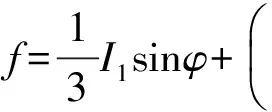
ccosφ=0

(7)

式中：φ为 内摩擦角，(°)；c为黏聚力，kPa；θ为应力Lode角，(°)；I1为应力张量第1不变量；J2为应力偏量第2不变量。其中：

I1=σx+σy+σz=σ1+σ2+σ3

(8)

(9)

Mohr-Coulomb屈服准则最大的优点是：简单实用，反映了土体抗剪强度不同的特性及静水压力的影响，黏聚力c和内摩擦角φ可以通过直接剪切试验测得。该方法的缺点是：屈服面是六边形，有棱角，数值计算很繁琐、收敛慢。为了避免产生计算的不便，ABAQUS采用连续光滑的椭圆等效屈服面代替角锥面。

3.4 流动法则的选取

在有限元计算中，采用关联流动法则还是非关联流动法则，取决于ψ值(剪胀角)。当ψ=φ时，为关联流动法则；当ψ≠φ时，为非关联流动法则[7],为提高计算的精度，本文采用非关联强度准则。

4 藏东南边坡稳定性数值计算

4.1 物理参数和计算模型的选取

本次试验选取了林芝市巴宜区S306旁一处滑坡体进行研究。该滑坡体天然含水率为9.53%。其基本物理参数如表1所示。

表1 土体强度特性参数E/MPaμγ/(kN·m-3)ρ/(g·cm-3)c/kPaφ/(°)500 25202 016 1922 63

本次边坡的模型选择坡度为45°，坡高为10 m，长度为20 m。该模型单元类型选择CPE4四节点平面应变单元进行分析，划分了349个单元，390个节点。边坡模型网格划分如图4所示。

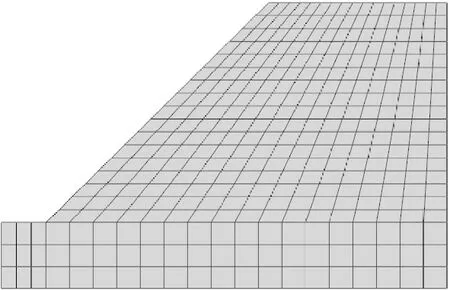
图4 边坡模型

4.2 模拟结果分析

4.2.1 边坡有限元模型的安全系数

利用ABAQUS提供的Combine函数功能，可绘制边坡左上角顶点的水平位移U1与强度折减系数FV1的变化关系。可以看出该特殊点位移发生突变时的强度折减系数，该折减系数就是有限元边坡模型的安全系数。FV1与U1的变化关系见图5。

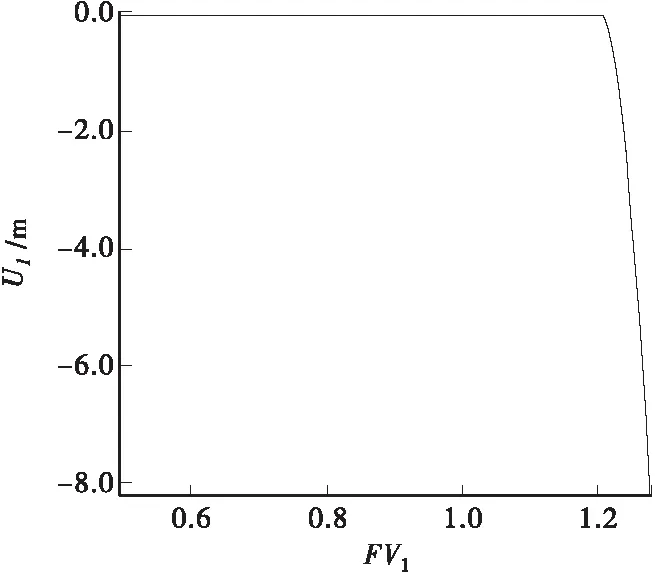
图5 FV1与U1的变化关系

从图5可以看出，强度折减系数FV1从0.5到1.2时，U1不发生变化。强度折减系数为1.207时，图形出现明显拐点，以特征点出现明显拐点作为边坡失稳评价标准，则该有限元边坡模型的安全系数为1.207。

4.2.2 边坡有限元模型塑性区域的发展情况

利用ABAQUS进行边坡稳定性有限元分析，可以清楚地知道塑性区域发展的情况。分析步t=0.2,t=0.35,t=0.462 5和t=0.472 8的分别绘制于图6、图7、图8、图9中。

在分析步t=0.2时，塑性区域从坡脚发生。随着强度折减系数的增加，塑性区域不断扩大，直到t=0.472 8时发展成为贯通整个边坡的塑性区域，对应的强度折减系数为1.209。若以边坡出现贯通的塑性区域作为边坡失稳的判别依据，则1.209为边坡失稳的安全系数。证明在天然含水率下边坡处于稳定状态。

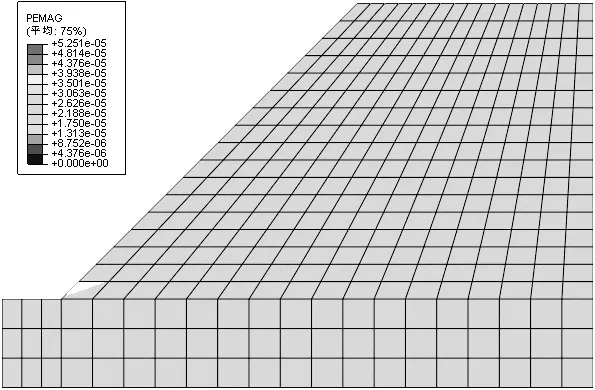
图6 t=0.2时塑性区域情况

图7 t=0.35时塑性区域情况

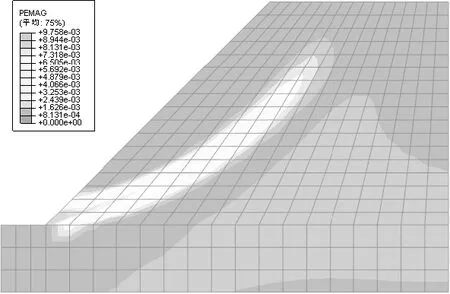
图8 t=0.462 5时塑性区域情况

图9 t=0.472 8时塑性区域情况

4.2.3 边坡有限元模型的滑动面

图10为计算不收敛时所对应的位移等值云图，从图中可以清楚地看出滑动面的位置。滑动面呈圆弧状通过坡脚贯通整个区域。形状与极限平衡分析法的结果是一致的。

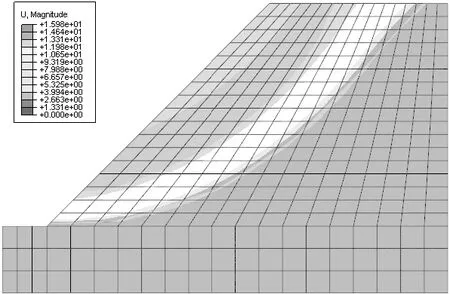
图10 位移等值云图

4.2.4 边坡滑动趋势

图11可以看出，在t=0.2时，边坡有向x轴负方向发展的趋势，出现从坡脚发生失稳。因而可以在坡脚设置挡土墙或者坡脚填土反压的方式，防止边坡失稳。

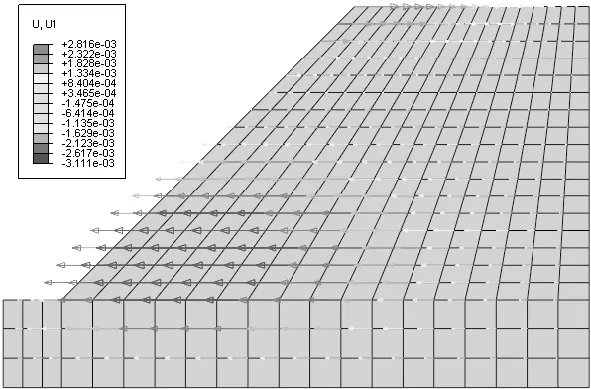
图11 滑坡趋势图

5 结论

1) 主要对滑坡体进行现场调研，对滑坡体所处位置的地形进行初步分析，认为漏斗状的地形，导致雨水容易聚集在滑坡体位置的土体中。藏东南在雨季时，降雨量较大，雨水在土体中不能及时排出，将会导致土体含水率过高，这为土坡失稳的发生创造了条件。

2) 通过击实试验，测出土体的最优含水率为15%。在含水率为15%时，试验土样的黏聚力和内摩擦角最大。含水率低于15%，随着含水率的增加，土样的黏聚力c和内摩擦角φ随之增加。黏聚力c增加的幅度较大。含水率高于15%，随着含水率的增加，土样黏聚力c和内摩擦角φ随之减少，两者减小的幅度较含水率增加时抗剪强度增加的值大。土样含水率对土样黏聚力c的影响较内摩擦角更加显著。

3) ABAQUS虽然没有内置强度折减法，但是实现起来也很简单。定义一个场变量，模型材料的参数随着这个场变量发生变化。基于ABAQUS的有限元强度折减法可以很好地进行边坡稳定性分析。该分析方法没有假定滑动面的位置，通过计算确定滑动面的位置，可以清楚地知道模型塑性区域的发展过程。该方法简单直观，可以为防止边坡失稳提供参考。

[1] 孙凤环,王培清.藏东南地区地热资源浅析[J].中国农村水利水电,1998(1)：38-40.

[2] 卢鲁,徐江,王培清.西藏藏东南地区公路路基受季节性冻融影响分析[J].公路工程,2015,40(1):23-28.

[3] 黄琨,万军伟,陈刚,等.非饱和土的抗剪强度与含水率关系的试验研究[J].岩土力学,2012,33(9):2600-2604.

[4] 李永亮,肖兵,李建举,等.含软弱夹层土坡稳定性分析研究[J].路基工程,2015(3):84-87.

[5] 裴利剑,屈本宁,钱闪光.有限元强度折减法边坡失稳判据的统一性[J].岩土力学,2010,31(10):3337-3341.

[6] 胡秀章,谷先广,李永池.修正的Mohr-Coulomb破坏准则在斜侵彻过程中的应用[J].中国科学技术大学学报,2008,38(11):1317-1321．

[7] 郑颖人,赵尚毅,张鲁渝．用有限元强度折减法进行边坡稳定分析[J].中国工程科学,2002,4(10):57-61.